VnDoc.com

Các dạng phương trình đường thẳng

Phương trình đường thẳng lớp 10

Bài trước

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Lý thuyết

Mức độ: Trung bình

Phân loại: Tài liệu Tính phí

Phương trình đường thẳng lớp 10

Trong môn Toán học, phương trình đường thẳng là một trong những chủ đề quan trọng và thường xuyên xuất hiện trong các bài thi, kiểm tra. Việc hiểu rõ các dạng phương trình đường thẳng giúp học sinh không chỉ giải quyết các bài toán hình học hiệu quả mà còn là tiền đề để học tốt các chuyên đề về hình học tọa độ, phương trình mặt phẳng trong không gian sau này. Bài viết này sẽ tổng hợp và phân tích các dạng phương trình đường thẳng cơ bản và nâng cao, từ phương trình tổng quát, phương trình tiếp tuyến, đến các dạng phương trình đặc biệt trong mặt phẳng tọa độ. Hãy cùng tìm hiểu chi tiết từng dạng và cách áp dụng chúng vào bài tập thực tế để dễ dàng làm quen với các kỹ thuật giải bài toán.

Loại 1: Các dạng phương trình đường thẳng

A. Tóm tắt lý thuyết

1. Phương trình tổng quát

* Định nghĩa: Phương trình: $\Delta :ax+by+c=0, a^{2}+b^{2}\neq 0$ là PTTQ của đường thẳng $\Delta$ nhận $\overrightarrow{n}\left ( a;b \right )$ làm vectơ pháp tuyến.

* Các dạng đặc biệt của phương trình đường thẳng.

$+)\ \Delta: ax+c=0, \left ( a\neq 0 \right )$ nên $\Delta$ song song hoặc trùng với Oy.

$+)\ \Delta: ay+c=0, \left ( a\neq 0 \right )$ nên $\Delta$ song song hoặc trùng với Ox.

$+)\ \Delta: ax+by=0, a^{2}+b^{2}\neq 0$ nên $\Delta$ đi qua gốc tọa độ.

+) Phương trình dạng đoạn chắn $\frac{x}{a}+\frac{y}{b}=1$ nên $\Delta$ qua A (a; 0) B(0;b) (ab khác 0)

+) Phương trình đường thẳng dạng hệ số góc y= kx+m (k được gọi là hệ số góc của đường thẳng)

Chú ý:

+) Ý nghĩa hình học của hệ số góc: Nếu $k \neq 0$ đặt $M = \Delta \cap Ox$ , gọi là nửa đường thẳng $\Delta$ ở phía trên . Khi đó $k = tan\widehat{xMt}$ . (Hình 1)

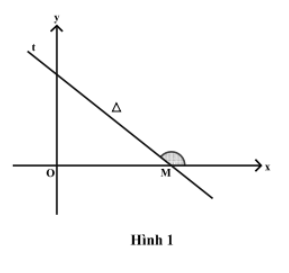
+) Điều kiện để phương trình đường thẳng có thể quy được về dạng hệ số góc: phương trình đường thẳng có thể đưa được về dạng hệ số góc nếu $b \neq 0$ .

Như vậy, đường thẳng có phương thẳng đứng không có dạng hệ số góc.

2. Phương trình tham số và phương trình chính tắc

Phương trình tham số:

Hệ $\left\{ \begin{matrix} x = x_{0} + at \\ y = y_{0} + bt \\ \end{matrix},\left( a^{2} + b^{2} \neq 0 \right) \right.$ là phương trình tham số của đường thẳng $\Delta$ qua $\left( x_{0};y_{0} \right)$ và nhận $\overrightarrow{u}(a;b)$ làm vectơ chỉ phương, với là tham số.

Phương trình tham số và phương trình chính tắc

Phương trình tham số: Hệ $\left\{ \begin{matrix} x = x_{0} + at \\ y = y_{0} + bt \\ \end{matrix},\left( a^{2} + b^{2} \neq 0 \right) \right.$ là PTTS của đường thẳng $\Delta$ qua $\left( x_{0};y_{0} \right)$ và nhận $\overrightarrow{u}(a;b)$ làm véc-tơ chỉ phương, với t là tham số.

Chú ý:

+) Ý nghĩa của phương trình tham số: - Thay mỗi $t \in R$ vào phương trình tham số, ta được một điểm $M(x;y) \in \Delta$ .

Điểm $M(x;y) \in \Delta$ thì có một số sao cho thỏa mãn hệ.

+) Một đường thẳng luôn có vô số PTTS.

Phương trình chính tắc: $\frac{x - x_{0}}{a} = \frac{y - y_{0}}{b}\ (ab \neq 0)$ là phương trình chính tắc của đường thẳng qua $M_{0}\left( x_{0};y_{0} \right)$ và nhận $\overrightarrow{u}(a;b)$ là một vectơ chi phương.

Một số bài toán cơ bản

Bài toán 1. Viết phương trình đường thẳng biết vectơ pháp tuyến và một điểm thuộc đường thẳng

$\left\{ \begin{matrix} \Delta\text{~qua~}M\left( x_{0};y_{0} \right) \\ \Delta\bot\overrightarrow{n}(a;b) \\ \end{matrix} \Leftrightarrow \Delta:a\left( x - x_{0} \right) + b\left( y - y_{0} \right) = 0 \right.$

Bài toán 2. Viết phương trình đường thẳng biết vectơ chi phương và một điểm thuộc đường thẳng

$\left\{ \begin{matrix} \Delta\text{~qua~}M(x_{0};y_{0}) \\ \Delta//\overrightarrow{u}(a;b) \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} \begin{matrix} \Delta\text{~qua~}M\left( x_{0};y_{0} \right) \\ \Delta\bot\overrightarrow{n}(b; - a) \\ \end{matrix} \\ \Leftrightarrow \Delta:b\left( x - x_{0} \right) - a\left( y - y_{0} \right) = 0 \\ \end{matrix} \right.\ \right.$

Bài toán 3. Viết phương trình đường thẳng đi qua một điểm và song song với một đường thẳng

$\left\{ \begin{matrix} \Delta\text{~qua~}M(x_{0};y_{0}) \\ \Delta//\Delta^{'}:ax + by + c = 0 \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} \begin{matrix} \Delta\text{~qua~}M\left( x_{0};y_{0} \right) \\ \Delta\bot\overrightarrow{n}(a;b) \\ \end{matrix} \\ \Leftrightarrow \Delta:a\left( x - x_{0} \right) + b\left( y - y_{0} \right) = 0,(M \notin \Delta) \\ \end{matrix} \right.\ \right.$

Bài toán 4. Viết phương trình đường thẳng đi qua một điểm và vuông góc với một đường thẳng

$\left\{ \begin{matrix} \Delta\text{~qua~}M(x_{0};y_{0}) \\ \Delta\bot\Delta^{'}:ax + by + c = 0 \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} \begin{matrix} \Delta quaM\left( x_{0};y_{0} \right) \\ \Delta\bot\overrightarrow{n}(b; - a) \\ \end{matrix} \\ \Leftrightarrow \Delta:b\left( x - x_{0} \right) - a\left( y - y_{0} \right) = 0 \\ \end{matrix} \right.\ \right.$

Bài toán 5: Viết phương trình đường thẳng đi qua một điểm và có hệ số góc cho trước

$\left\{ \begin{gathered} \Delta {\text{ }}qua{\text{ }}M\left( {{x_0};{y_0}} \right) \hfill \\ \Delta {\text{ co he so goc k}} \hfill \\ \end{gathered} \right. \Rightarrow \Delta :y = k\left( {x - {x_0}} \right) + {y_0}$

Bài toán 6. Viết phương trình đường thẳng đi qua hai điểm

Đường thẳng đi qua hai điểm và chính là đường thẳng đi qua và nhận vectơ $\overrightarrow{AB}$ làm vectơ chỉ phương (Bài toán 2).

Bài toán 7. Viết phương trình đường trung trực của một đoạn thẳng

Quy về Bài toán 1: trung trực của đoạn thẳng chính là đường thẳng đi qua trung điểm của đoạn thẳng này và nhận $\overrightarrow{AB}$ làm vectơ pháp tuyến.

Bài toán 8. Viết phương trình đường thẳng đi qua một điểm và tạo với góc cho trước

$\Delta$ đi qua $M\left( x_{0};y_{0} \right)$ và tạo với góc $\alpha\left( 0^{\circ} < \alpha < 90^{\circ} \right) \Leftrightarrow \left\{ \begin{matrix} \Delta:y = k\left( x - x_{0} \right) + y_{0} \\ k = \pm tan\alpha \end{matrix} \right.$ .

Bài toán 9. Tìm hình chiếu vuông góc của một điểm lên một đường thẳng

Giả sử cần tìm hình chiếu của điểm lên đường thẳng $\Delta$ , ta làm như sau

Lập phương trình đường thẳng $\Delta'$ qua , vuông góc với $\Delta$ (Bài toán 4).
là hình chiếu vuông góc của lên $\Delta \Leftrightarrow H = \Delta \cap \Delta'$ .

Bài toán 10. Tìm điểm đối xứng với một điểm qua một đường thẳng

Giả sử cần tìm điểm đối xứng với điểm qua đường thẳng $\Delta$ , ta làm như sau

Tìm hình chiếu cùa điểm lên đường thẳng $\Delta$ (Bài toán 9 )
đối xứng với qua $\Delta' \Leftrightarrow M'$ đối xứng với qua .
B. Một số ví dụ

Ví dụ 1. Đưa các phương trình đường thẳng sau đây về dạng tổng quát

$\Delta:x = 2$ .
$\Delta:\frac{x}{2} + \frac{y}{3} = 1$ .
$\Delta:y =$
$\Delta:\frac{x - 1}{7} = \frac{y + 2}{5}$ .
$\Delta:\left\{ \begin{matrix} x = 1 + 2t \\ y = - 2 + 5t \end{matrix} \right.$ .
$\Delta:\left\{ \begin{matrix} x \\ y \end{matrix} \right.$
$\Delta:x = 2 \Leftrightarrow \Delta:x - 2 = 0$ .
$\Delta:\frac{x}{2} + \frac{y}{3} = 1 \Leftrightarrow \Delta:3x + 2y - 6 = 0$ .
$\Delta:y = \frac{1}{2}x + 7 \Leftrightarrow \Delta:x - 2y + 14 = 0$ .
$\Delta:\frac{x - 1}{7} = \frac{y + 2}{5} \Leftrightarrow \Delta:5x - 7y - 19 = 0$ .
$\Delta:\left\{ \begin{matrix} x = 1 + 2t \\ y = - 2 + 5t \end{matrix} \Leftrightarrow \Delta:\frac{x - 1}{2} = \frac{y + 2}{5} \Leftrightarrow \Delta:5x - 2y - 9 = 0 \right.$ .
$\Delta:\left\{ \begin{matrix} x = 1 + 2t \\ y = - 2 \end{matrix} \Leftrightarrow \Delta:y = - 2 \Leftrightarrow \Delta:y + 2 = 0 \right.$ .

$\Delta$ qua và nhận $\overrightarrow{n}(3; - 1)$ làm vectơ pháp tuyến.
$\Delta$ qua $M\left( - \frac{1}{2};3 \right)$ và nhận $\overrightarrow{u}(2;0)$ làm vectơ chỉ phương.
$\Delta$ qua và song song với đường thẳng $\Delta':x - 2y + 12 = 0$ .
$\Delta$ qua $M\left( 1; - \frac{3}{4} \right)$ và vuông góc với đường thẳng $\Delta': - x - 3y + 12 = 0$ .
$\Delta$ qua và có hệ số góc bằng .
$\Delta$ đi qua hai điểm và .
$\Delta$ đi qua hai điểm và .
$\Delta$ là trung trực của đoạn thẳng với hai đầu mút và .

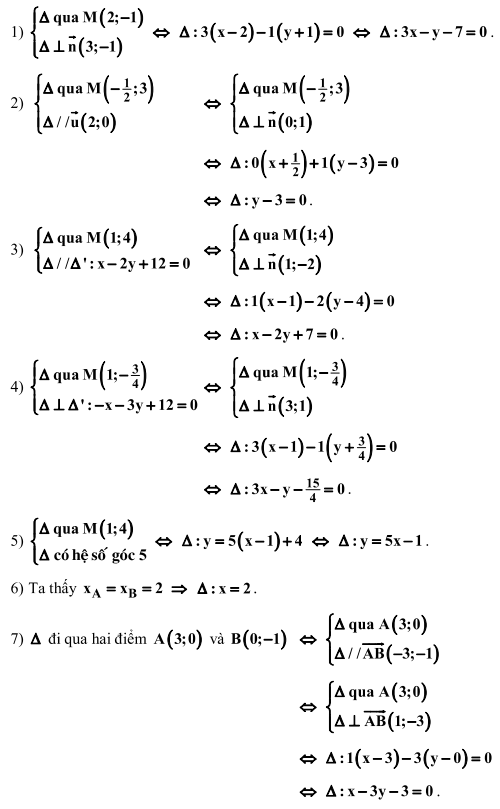
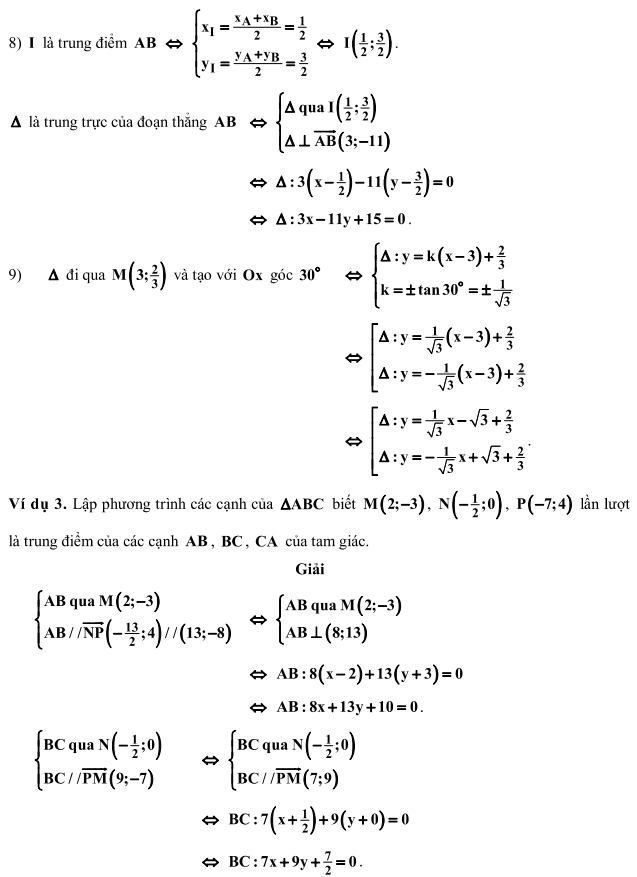
Các dạng phương trình đường thẳng

.........................................

Nắm vững các dạng phương trình đường thẳng không chỉ giúp bạn giải quyết các bài toán hình học cơ bản mà còn là bước đệm quan trọng để tiếp cận các kiến thức nâng cao trong toán học như phương trình mặt phẳng và không gian. Việc hiểu rõ các dạng phương trình này giúp bạn dễ dàng nhận diện dạng bài và tìm được hướng giải quyết tối ưu. Hy vọng qua bài viết này, bạn đã có cái nhìn tổng quan về các phương trình đường thẳng và cách vận dụng chúng một cách linh hoạt trong học tập. Đừng quên luyện tập thật nhiều với các bài tập thực tế để nâng cao kỹ năng giải toán của mình.

Luyện tập mở rộng

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Bon

1

4.278

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!