Đề thi HK1 Toán 10 Cánh Diều (theo CV 7991) Đề 3

Đề kiểm tra HK1 Toán 10 sách Cánh Diều (Theo CV 7991) có đáp án

Bạn đang tìm Đề thi HK1 Toán 10 Cánh Diều (theo công văn 7991) – Đề 3 kèm đáp án chi tiết để ôn tập hiệu quả cho kỳ thi học kì 1? Bộ đề dưới đây được biên soạn bám sát cấu trúc, chuẩn kiến thức – kỹ năng theo chương trình mới, giúp học sinh luyện tập, củng cố kiến thức và cải thiện điểm số. Với đáp án và hướng dẫn giải chi tiết, bài viết sẽ hỗ trợ bạn tự kiểm tra năng lực và rút kinh nghiệm chính xác nhất.

Họ và tên học sinh: …………………………….. Lớp: …………………………..

A. TRẮC NGHIỆM (7 ĐIỂM)

Phần I. Câu trắc nghiệm nhiều phương án lựa chọn (3 điểm)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Trong mặt phẳng tọa độ \(Oxy,\) cho hai điểm \(A(3; - 1)\) và \(B(2;10).\) Tính tích vô hướng \(\overrightarrow{AO}.\overrightarrow{OB}\)

A. \(\overrightarrow{AO}.\overrightarrow{OB} = - 4\).               B. \(\overrightarrow{AO}.\overrightarrow{OB} = 0\).       C. \(\overrightarrow{AO}.\overrightarrow{OB} = 4\).     D. \(\overrightarrow{AO}.\overrightarrow{OB} = 16\).

Câu 2: Điểm nào sau đây không thuộc đồ thị hàm số \(y = \frac{\sqrt{x^{2} - 4x + 4}}{x}.\)

A. \(A(1; - 1).\)      B. \((2;0).\)      C. \(\left( 3;\frac{1}{3} \right).\)           D. \(D( - 1; - 3).\)

Câu 3: Hai vectơ được gọi là bằng nhau khi và chỉ khi:

A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau;

B. Giá của chúng song song nhau và độ dài của chúng bằng nhau;

C. Chúng ngược hướng và độ dài của chúng bằng nhau.

D. Chúng có cùng hướng và độ dài của chúng bằng nhau.

Câu 4: Đỉnh của parabol \((P):y = 3x^{2} - 2x + 1\) là:

A. \(I\left( - \frac{1}{3};\frac{2}{3} \right)\).      B. \(I\left( - \frac{1}{3}; - \frac{2}{3} \right)\).      C. \(I\left( \frac{1}{3}; - \frac{2}{3} \right)\).      D. \(I\left( \frac{1}{3};\frac{2}{3} \right)\).

Câu 5: Cho hàm số \(y = ax^{2} + bx + c\) có đồ thị như hình bên.

Chọn phát biểu đúng.

A. \(f(x) < 0 \Leftrightarrow x \in \lbrack 1;4\rbrack\)                          B. \(f(x) < 0 \Leftrightarrow x \in (1;4)\)

C. \(f(x) < 0 \Leftrightarrow x \in \left( - \infty;1) \cup (4; + \infty \right)\)    D. \(f(x) \geq 0 \Leftrightarrow x \in \left( - \infty;1) \cup (4; + \infty \right)\)

Câu 6: Tập nghiệm của bất phương trình \(- 3x^{2} + 2x + 1 < 0\) là:

A. \(S = ( - \infty; - \frac{1}{3})\)            B. \(S = (1; + \infty)\)

C. \(S = \left( - \frac{1}{3};1 \right)\)             D. \(S = ( - \infty; - \frac{1}{3}) \cup (1; + \infty)\)

Câu 7: Miền nghiệm của bất phương trình \(x + 2y < 3\) là phần không tô đậm (không kể đường thẳng) là hình nào trong các hình vẽ dưới đây?

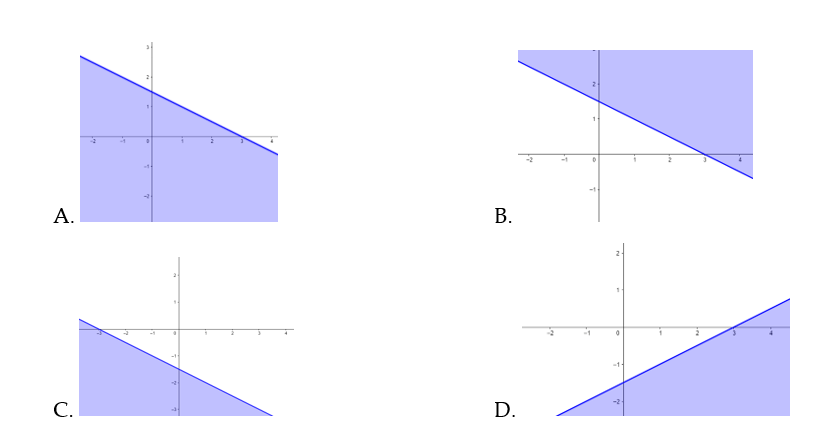
Câu 8: Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây đúng?

A. \(\overrightarrow{AC} - \overrightarrow{AD} = \overrightarrow{CD}\).             B. \(\overrightarrow{AC} - \overrightarrow{BD} = 2\overrightarrow{CD}\).

C. \(\overrightarrow{AC} + \overrightarrow{BC} = \overrightarrow{AB}\).             D. \(\overrightarrow{AC} + \overrightarrow{BD} = 2\overrightarrow{BC}\).

Câu 9. Trong mặt phẳng tọa độ \(Oxy\) cho các điểm \(A(1;3)\),\(B(4;0)\),\(C(2; - 5)\). Tọa độ điểm \(M\) thỏa mãn \(\overrightarrow{MA} + \overrightarrow{MB} - 3\overrightarrow{MC} = \overrightarrow{0}\) là

A. \(M(1;18)\).            B. \(M( - 1;18)\).            C. \(M( - 18;1)\).      D. \(M(1; - 18)\).

Câu 10. Trong mặt phẳng tọa độ \(Oxy\), cho \(\overrightarrow{a} = ( - 1;2)\), \(\overrightarrow{b} = (3;2)\). Tọa độ của vectơ \(\overrightarrow{v} = - 2\overrightarrow{a} + 3\overrightarrow{b}\) là

A. \(\overrightarrow{v} = (8;2)\).         B. \(\overrightarrow{v} = (11;8)\).        C. \(\overrightarrow{v} = (11;2)\).     D. \(\overrightarrow{v} = (2;4)\).

Câu 11. Trong các mệnh đề sau, mệnh đề nào đúng?

A. \(\forall x\mathbb{\in R},x^{2} \geq x.\)                                             B. \(\forall x\mathbb{\in R},x > 1 \Rightarrow x^{2} > x.\)

C. \(\forall n\mathbb{\in R},n\) và \(n + 2\) là các số nguyên tố        D. \(\forall n\mathbb{\in N}\), nếu n lẻ thì \(n^{2} + n + 1\) là số nguyên tố

Câu 12. Cho \(A = \lbrack 0;3\rbrack;\ \ B = (1;5);\ \ C = (0;1)\). Khẳng định nào sau đây sai?

A. \(A \cap B \cap C = \varnothing.\)                     B. \(A \cup B \cup C = \lbrack 0;5).\)

C. \((A \cup C)\backslash C = (1;5).\)              D. \((A \cap B)\backslash C = (1;3\rbrack.\)

Phần 2. Câu trắc nghiệm đúng sai (2 điểm)

Thí sinh trả lời câu 13 và câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 13 (1 điểm): Cho biết \(226\ g\) thịt bò chứa khoảng \(59\ g\) protein. Một quả trứng nặng \(46\ g\) có chứa khoảng \(6\ g\) protein. Giả sử có một người mỗi ngày cần không quá \(60\ g\) protein. Gọi số gam thịt bò và số gam trứng mà người đó ăn trong một ngày lần lượt là \(x,y\).

Phát biểu	Đúng	Sai
a) Số gam protein từ thịt bò là \(\frac{59}{226}x\); số gam protein từ trứng là \(\frac{6}{46}y\).
b) Bất phương trình theo \(x,y\) diễn tả giới hạn về lượng protein mà người đó cần mỗi ngày là \(\frac{59}{226}x + \frac{3}{23}y \geq 60\).
c) Cặp số \((150;92)\) là một nghiệm của bất phương trình theo \(x,y\) diễn tả giới hạn về lượng protein mà người đó cần mỗi ngày.
d) Nếu người đó ăn \(200\ g\) thịt bò và 2 quả trứng, mỗi quả \(46\ g\), trong một ngày thì phù hợp.

Câu 14 (1 điểm): Cho tam giác \(ABC\), biết \(AB = 4\), \(BC = 5\), \(\widehat{B} = 120{^\circ}\). Xét tính đúng sai của các khẳng định dưới đây:

Phát biểu	Đúng	Sai
a) \(\widehat{A} > \widehat{C}\).
b) \(AC = \sqrt{61}\).
c) Độ dài đường cao\(ABC\) hạ từ đỉnh \(B\) là \(2,23\).
d) Bán kính đường tròn nội tiếp của tam giác \(ABC\) là \(1,03\).

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2 điểm)

Trong mỗi câu hỏi từ 15 đến 18, hãy viết câu trả lời đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 15. Cho các tập hợp khác rỗng \(A = \lbrack m\ ;\ m + 3\rbrack\) và \(B = ( - 2\ ;\ 4\rbrack\). Số giá trị nguyên của \(m\) để \(A \cap B \neq \varnothing\) là:

Trả lời:

Câu 16. Cho các số thực \(x,y\) thỏa mãn bất phương trình \(5x^{2} + 5y^{2} - 5x - 15y + 8 \leq 0\). Tìm giá trị nhỏ nhất của biểu thức \(S = x + 3y.\)

Trả lời:

Câu 17. Một người nông dân thả 1000 con cá giống vào hồ nuôi vừa mới đào. Biết rằng sau mỗi năm thì số lượng cá trong hồ tăng thêm \(x\) lần số lượng cá ban đầu và \(x\) không đổi. Bằng cách thay đổi kĩ thuật nuôi và thức ăn cho cá. Hỏi sau hai năm để số cá trong hồ là 36000 con thì tốc độ tăng số lượng cá trong hồ là bao nhiêu? Biết tốc độ tăng mỗi năm là không đổi.

Trả lời:

Câu 18. Cho M là một điểm nằm trên đường tròn ngoại tiếp tam giác \(\Delta ABC\) đều cạnh \(2a\). Tìm độ dài của vectơ \(\overrightarrow{u} = \overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC}.\)

Trả lời:

B. TỰ LUẬN (3 ĐIỂM)

Bài 1 (1 điểm). a) Tìm tập xác định của hàm số \(y = \sqrt{2x^{2} - 5x + 2}\)?

b) Với giá trị nào của \(m\) thì phương trình: \((m - 1)x^{2} - 2(m - 2)x + m - 3 = 0\) có hai nghiệm \(x_{1},x_{2}\) thỏa mãn \(x_{1} + x_{2} + x_{1}x_{2} < 1\)?

Bài 2 (1,5 điểm). Cho các điểm \(A( - 1; - 1)\), \(B(3;1)\), \(C(6;0)\).

a) Chứng minh ba điểm \(A,\ B,\ C\) không thẳng hàng.

b) Tính góc \(B\) và diện tích tam giác \(ABC\).

Bài 3 (0,5 điểm). Gia đình bác Tuân dự định trồng cà phê và sầu riêng trên diện tích 8 ha. Nếu trồng cà phê thì cần 20 công và thu 3 triệu đồng trên diện tích mỗi ha, nếu trồng sầu riêng thì cần 30 công và thu 4 triệu đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được lợi nhuận cao nhất biết rằng tổng số công không quá 180?

- Hết -

Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!