Đề thi HK1 Toán 10 Kết nối tri thức (theo công văn 7991) Đề 3

Đề kiểm tra HK1 Toán 10 KNTT (Theo CV 7991) có đáp án

Bạn đang tìm Đề thi HK1 Toán 10 Kết nối tri thức (theo công văn 7991) – Đề 3 kèm đáp án chi tiết để ôn tập hiệu quả cho kỳ thi học kì 1? Bộ đề dưới đây được biên soạn bám sát cấu trúc, chuẩn kiến thức – kỹ năng theo chương trình mới, giúp học sinh luyện tập, củng cố kiến thức và cải thiện điểm số. Với đáp án và hướng dẫn giải chi tiết, bài viết sẽ hỗ trợ bạn tự kiểm tra năng lực và rút kinh nghiệm chính xác nhất.

Họ và tên học sinh: …………………………….. Lớp: …………………………..

A. TRẮC NGHIỆM (7 ĐIỂM)

Phần I. Câu trắc nghiệm nhiều phương án lựa chọn (3 điểm)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Biết \(\overline{b} = \frac{2 - \sqrt{5}}{3} = - 0,0786893....\). Số gần đúng của \(\overline{b}\) với độ chính xác \(d = 0,024\) là:

A. \(- 0,103\).            B. \(- 0,08\).            C. \(- 0,079\).        D. \(- 0,055\).

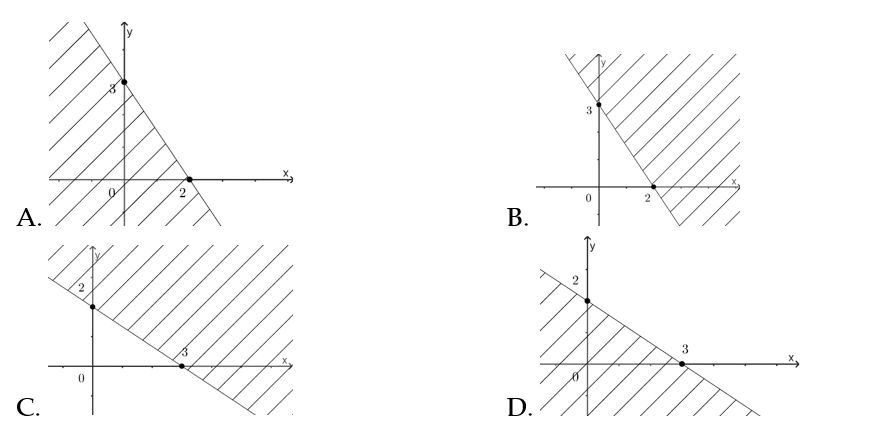
Câu 2: Bất phương trình \(2x + 3y \geq 6\) có biểu diễn miền nghiệm (miền không gạch chéo) là hình nào trong các hình dưới đây?

Câu 3: Cho mẫu số liệu:

Độ lệch chuẩn của mẫu số liệu trên gần với giá trị nào sau đây?

A. \(8,86\).            B. \(8,62\).        C. \(2,98\).               D. \(2,94\).

Câu 4: Bất phương trình nào sau đây không là bất phương trình bậc nhất hai ẩn?

A. \(x + y^{2} - 2 < 0\).          B. \(2x - 5y + 1 \leq 0\).      C. \(y \geq 1\).          D. \(x + 2y > 0\).

Câu 5: Cho mẫu số liệu: \(23,20,41,73,29,23\). Số trung bình của mẫu số liệu trên gần với giá trị nào sau đây?

A. \(20,14\).          B. \(34,83\).        C. 18,39.              D. \(26\).

Câu 6: Cho hình vuông \(ABCD\), khi đó \(\left( \overrightarrow{DC},\overrightarrow{BA} \right)\) bằng

A. \(\left( \overrightarrow{DC},\overrightarrow{BA} \right) = 180^{0}\).                 B. \(\left( \overrightarrow{DC},\overrightarrow{BA} \right) = 135^{0}\).

C. \(\left( \overrightarrow{DC},\overrightarrow{BA} \right) = 45^{0}\).                   D. \(\left( \overrightarrow{DC},\overrightarrow{BA} \right) = 0^{0}\).

Câu 7: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A. \(\exists x\mathbb{\in N},\ x^{2} = 3\).                       B. \(\forall n\mathbb{\in N},n^{2} - n \geq 0\).

C. \(\forall x\mathbb{\in N},(x - 2)^{2} < x^{2}\).             D. \(\exists n\mathbb{\in N},3^{n} < n + 3\).

Câu 8: Vectơ \(\overrightarrow{a} = ( - 4;0)\) được phân tích theo hai vectơ đơn vị như thế nào?

A. \(\overrightarrow{a} = - 4\overrightarrow{i} + \overrightarrow{j}\).                       B. \(\overrightarrow{a} = - \overrightarrow{i} + 4\overrightarrow{j}\).

C. \(\overrightarrow{a} = - 4\overrightarrow{j}\).                                D. \(\overrightarrow{a} = - 4\overrightarrow{i}\).

Câu 9: Biết \(\left| \overrightarrow{a} \right| = \sqrt{2},\ \ \ \left| \overrightarrow{b} \right| = 1\) và \(\overrightarrow{a}.\overrightarrow{b} = - 1\). Khi đó \(\left( \overrightarrow{a},\overrightarrow{b} \right)\) bằng:

A. \(60^{0}\).                  B. \(135^{0}\).      C. \(180^{0}\).                 D. \(45^{0}\).

Câu 10: Cặp số nào sau đây là nghiệm của bất phương trình \(2x - 3y + 2 \geq 0\) ?

A. \((3;3)\).         B. \((2;3)\).            C. \(( - 4; - 2)\).          D. \((0;4)\).

Câu 11: Ký hiệu H là tập hợp các học sinh của lớp 10A. T  là tập hợp các học sinh nam, G là tập hợp các học sinh nữ của lớp 10A. Khẳng định nào sau đây sai?

A. \(T \cup G = H\)            B. \(T \cap G = \varnothing\)               C. \(H\backslash T = G\)            D. \(G\backslash T = \varnothing\)

Câu 12: Một người dùng một lực \(\overrightarrow{F}\) có độ lớn \(60\ N\) kéo một vật dịch chuyển một đoạn \(50m\). Biết rằng lực \(\overrightarrow{F}\) hợp với hướng dịch chuyển một góc \(60^{0}\). Công sinh bởi lực \(\overrightarrow{F}\) bằng

A. \(1500\sqrt{3}\ J\).                B. \(1200\ J\).                 C. \(1500\ J\).                         D. \(3000\ J\).

Phần 2. Câu trắc nghiệm đúng sai (2 điểm)

Thí sinh trả lời câu 13 và câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 13 (1 điểm): Bảng sau đây cho biết số chỗ ngồi của một số sân vận động được sử dụng trong Giải Bóng đá Vô địch Quốc gia Việt Nam năm \(2022\):

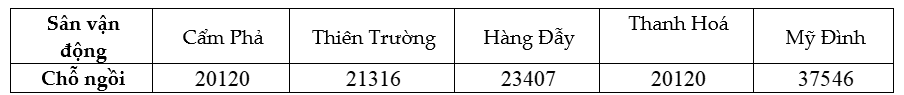
Xét tính đúng sai của các câu sau:

Phát biểu	Đúng	Sai
a) Mốt của mẫu số liệu trên là \(20120\).
b) Trung vị của mẫu số liệu trên là \(23407\).
c) Số chỗ ngồi đã được sử dụng rung bình của \(5\)sân đó là \(24502\).
d) Nếu bỏ đi số liệu chỗ ngồi của Sân vân động Quốc gia Mỹ Đình thì mốt không thay đổi số trung bình và trung vị sẽ thay đổi.

Câu 14 (1 điểm): Cho tam giác \(ABC\) có \(AB = 7\), \(AC = 8\), \(BC = \sqrt{57}\). Xét tính đúng sai của các mệnh đề sau:

Phát biểu	Đúng	Sai
a) \(\cos\widehat{A}\ = \frac{1}{2}\)
b) \(S_{\Delta ABC} = 14\sqrt{3}\) .
c) Bán kính đường tròn ngoại tiếp tam giác \(ABC\) bằng \(2\sqrt{19}\) .
d) Trên tia đối của tia \(AC\) lấy điểm \(D\) sao cho \(AD = \frac{1}{4}AC\). Khi đó: \(BD = \sqrt{76}\).

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2 điểm)

Trong mỗi câu hỏi từ 15 đến 18, hãy viết câu trả lời đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 15. Cho tập \(A = \left\lbrack m^{2} + 2m;m^{2} + 2m + 1 \right\rbrack\) và \(B = \lbrack 2m - 1;2m + 5)\). Có tất cả bao nhiêu số \(m\) nguyên để \(A \subset B\)?

Trả lời:

Câu 16. Một sân pickleball có dạng hình chữ nhật với chiều dài và chiều rộng của sân lần lượt là \(13,41\ m\) và \(6,1\ m\). Bạn 1 và bạn 2 tính độ dài đường chéo của sân pickleball đó rồi cho kết quả lần lượt là \(c_{1} = 14,74\ m\) và \(c_{2} = 14,75\ m\). Hỏi bạn nào cho kết quả chính xác hơn?

Trả lời:

Câu 17. Biểu đồ dưới đây biểu diễn lợi nhuận mà bốn chi nhánh A,B,C,D của một doanh nghiệp thu được trong hai năm 2020 và 2021.

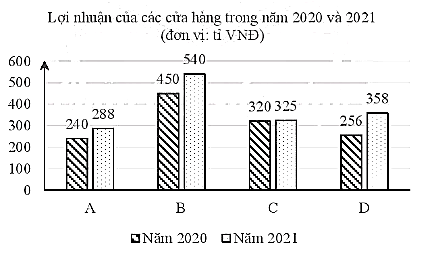
So với năm 2020, bao nhiêu chi nhánh có tỷ lệ lợi nhuận thu được năm 2021 vượt 20%?

Trả lời:

Câu 18. Khoảng cách từ \(A\) đến \(B\) không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm \(C\) mà từ đó có thể nhìn được \(A\) và \(B\) dưới một góc \(78^{o}24'\) . Biết \(CA = 250m,CB = 120m\). Khoảng cách \(AB\) bằng bao nhiêu?

Trả lời:

B. TỰ LUẬN (3 ĐIỂM)

Bài 1 (1 điểm). Một phân xưởng sản xuất hai loại sản phẩm. Thời gian để làm ra một sản phẩm loại I gấp hai lần thời gian làm ra một sản phẩm loại II. Nếu chỉ sản xuất toàn sản phẩm loại II thì trong 1 giờ phân xưởng làm được 60 sản phẩm. Phân xưởng làm việc 8 tiếng mỗi ngày và thị trường tiêu thụ tối đa trong một ngày là 200 sản phẩm loại I và 240 sản phẩm loại II. Tiền lãi khi bán một sản phẩm loại I là 24 nghìn đồng, một sản phẩm loại II là 15 nghìn đồng. Khi tiền lãi lớn nhất, tổng số sản phẩm loại I và loại II là bao nhiêu?

Bài 2 (1 điểm). Cho tam giác \(ABC\) có \(A(1;2),\ \ B( - 2;6),\ \ C(9;8)\).

a) Chứng minh tam giác \(ABC\) vuông tại \(A\).

b) Tính góc \(B\) của tam giác \(ABC\).

c) Xác định hình chiếu của \(A\) lên cạnh \(BC\).

Bài 3 (1 điểm). Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một sản phẩm của một số thí sinh ở bảng sau:

a) Hãy tìm số trung bình, tứ phân vị và mốt của thời gian thi nghề của các thí sinh trên.

b) Năm ngoái, thời gian thi của các thí sinh có số trung bình và trung vị đều bằng \(7\). Bạn hãy so sánh thời gian thi nói chung của các thí sinh trong hai năm.

- Hết -

 Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!