Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Cách tìm tọa độ điểm, tọa độ vectơ trong mặt phẳng Oxy

Bài tập Tọa độ vectơ Toán 10 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại: Tài liệu Lẻ

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Cách xác định tọa độ vectơ trong Oxy

A. Cách tìm tọa độ điểm trong mặt phẳng Oxy
B. Bài tập minh họa tìm tọa độ điểm tọa độ vectơ trên hệ tọa độ Oxy
C. Bài tập tự rèn luyện tìm tọa độ điểm trong mặt phẳng Oxy có đáp án
D. Đáp án bài tập tự rèn luyện

Trong chương trình Toán 10, chuyên đề tọa độ điểm và tọa độ vectơ trong mặt phẳng Oxy là nền tảng quan trọng giúp học sinh làm quen với kiến thức hình học tọa độ. Việc hiểu rõ cách xác định tọa độ điểm, tọa độ vectơ và mối quan hệ giữa chúng giúp bạn giải quyết hiệu quả các bài toán về vectơ, trung điểm, khoảng cách hay phương trình đường thẳng. Bài viết này sẽ hướng dẫn chi tiết cách tìm tọa độ điểm, tọa độ vectơ, kèm ví dụ minh họa và bài tập có đáp án, giúp bạn học nhanh – hiểu sâu – vận dụng linh hoạt.

A. Cách tìm tọa độ điểm trong mặt phẳng Oxy

Để tìm tọa độ của vectơ $\overrightarrow{a}$ ta làm như sau:

Dựng vectơ $\overrightarrow{OM} = \overrightarrow{a}$ .
Gọi H; K lần lượt là hình chiếu vuông góc của M lên Õ; Oy. Khi đó $\overrightarrow{a}\left( a_{1};a_{2} \right)$ với $a_{1} = \overline{OH},\ \ a_{2} = \overline{OK}$
Để tìm tọa độ điểm A ta đi tìm tọa độ vectơ $\overrightarrow{OA}$ .
Nếu biết tọa độ hai điểm $A(x_{A};y_{A}),B(x_{B};y_{B})$ suy ra tọa độ $\overrightarrow{AB}$ được xác định theo công

thức $\overrightarrow{AB} = \left( x_{B} - x_{A};y_{B} - y_{A} \right)$

Chú ý: $\overline{OH} = OH$ nếu H nằm trên tia Ox (hoặc Oy) và $\overline{OH} = - OH$ nếu H nằm trên tia đối tia Ox (hoặc Oy).

B. Bài tập minh họa tìm tọa độ điểm tọa độ vectơ trên hệ tọa độ Oxy

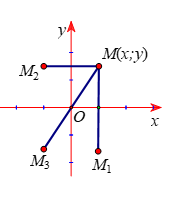
Ví dụ 1: Trong mặt phẳng tọa độ Oxy. Cho điểm M(x; y). Tìm tọa độ của các điểm

a) M₁ đối xứng với M qua trục hoành.

b) M₂ đối xứng với M qua trục tung.

c) M₃ đối xứng với M qua gốc tọa độ.

Hướng dẫn giải

Hình vẽ minh họa:

a) M₁ đối xứng với M qua trục hoành suy ra $M_{1}(x; - y)$ .

b) M₂ đối xứng với M qua trục tung suy ra $M_{2}( - x;y)$ .

c) M₃ đối xứng với M qua gốc tọa độ suy ra $M_{3}( - x; - y)$ .

Ví dụ 2: Trong hệ trục tọa độ (O; $\overrightarrow{i}$ ; $\overrightarrow{j}$ ), cho hình vuông ABCD tâm I và có A(1; 3). Biết điểm B thuộc trục (O; $\overrightarrow{i}$ ) và $\overrightarrow{BC}$ cùng hướng với $\overrightarrow{i}$ . Tìm tọa độ các vectơ $\overrightarrow{AB},\ \ \overrightarrow{BC}$ và $\overrightarrow{AC}$ .

Hướng dẫn giải

Hình vẽ minh họa:

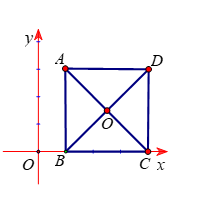
Từ giả thiết ta xác định được hình vuông trên mặt phẳng tọa độ (như hình vẽ)

Vì điểm A(1; 3) suy ra AB = 3; OB = 1.

Do đó B(1; 0), C(4; 0), D(4; 3)

Vậy $\overrightarrow{AB}(0; - 3),\ \ \overrightarrow{BC}(3;0)$ và $\overrightarrow{AC}(3; - 3)$ .

Ví dụ 3: Trong mặt phẳng tọa độ Oxy. Cho hình thoi ABCD cạnh a và $\widehat{BAD} = 60^{0}$ . Biết A trùng với gốc tọa độ O, C thuộc trục Ox và $x_{B} \geq 0,\ y_{B} \geq 0$ . Tìm tọa độ các đỉnh của hình thoi ABCD.

Hướng dẫn giải

Hình vẽ minh họa:

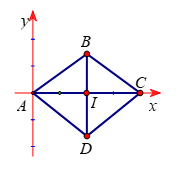
Từ giả thiết ta xác định được hình thoi trên mặt phẳng tọa độ Oxy

Gọi I là tâm hình thoi ta có:

$BI = AB\sin\widehat{BAI} = asin30^{0} = \frac{a}{2}$

$AI = \sqrt{AB^{2} - BI^{2}} = \sqrt{a^{2} - \frac{a^{2}}{4}} = \frac{a\sqrt{3}}{2}$

Suy ra $A(0;0),\ \ B\left( \frac{a\sqrt{3}}{2};\frac{a}{2} \right),\ \ C\left( a\sqrt{3};0 \right),\ \ D\left( \frac{a\sqrt{3}}{2}; - \frac{a}{2} \right)$ .

Ví dụ 4: Trong mặt phẳng tọa độ Oxy, cho các vectơ $\overrightarrow{a} = 3\overrightarrow{i} - 2\overrightarrow{j},\ \overrightarrow{b} = (4; - 1)$ và các điểm M(-3;6), N(3;-3).

a) Tìm mối liên hệ giữa các vectơ $\overrightarrow{MN}$ và $2\overrightarrow{a} - \ \overrightarrow{b}$

b) Các điểm O, M, N có thẳng hàng hay không?

c) Tìm điểm P(x;y) để OMPN là hình bình hành.

Hướng dẫn giải

a) Ta có $\overrightarrow{a} = (3; - 2)$ . $2\overrightarrow{a} - \ \overrightarrow{b} = (2.3 - 4;2.( - 2) + 1) = (2; - 3).$

và $\overrightarrow{MN} = (6; - 9)$

Vậy $\overrightarrow{MN} = 3(2\overrightarrow{a} - \ \overrightarrow{b})$

b) Ta có $\overrightarrow{OM} = ( - 3;5),\ \ \overrightarrow{ON} = (3; - 3)$

Vì $\frac{- 3}{3} \neq \frac{6}{- 3}$ nên hai vectơ $\overrightarrow{OM},\ \ \ \overrightarrow{ON}$ không cùng phương. Suy ra các điểm O, M, N không cùng nằm trên một đường thẳng. Do đó O, M, N không thẳng hàng.

c) Các điểm O, M, N không thẳng hàng

Để OMNP là hình bình hành khi và chỉ khi $\overrightarrow{OM} = \ \overrightarrow{PN}$

Gọi P(x; y)

Ta có $\overrightarrow{OM} = ( - 3;5),\ \ \overrightarrow{PN} = (3 - x; - 3 - y)$ . Suy ra

$\left\{ \begin{matrix} - 3 = 3 - x \\ 6 = - 3 - y \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 6 \\ y = - 9 \end{matrix} \right.$

Vậy điểm cần tìm là P(6;-9).

C. Bài tập tự rèn luyện tìm tọa độ điểm trong mặt phẳng Oxy có đáp án

Bài tập 1: Trong hệ trục tọa độ (O; $\overrightarrow{i}$ ; $\overrightarrow{j}$ ), Cho tam giác đều ABC cạnh a, biết O là trung điểm BC, $\overrightarrow{i}$ cùng hướng với $\overrightarrow{OC}$ , $\overrightarrow{j}$ cùng hướng $\overrightarrow{OA}$ .

a) Tính tọa độ của các đỉnh của tam giác ABC.

b) Tìm tọa độ trung điểm E của AC.

c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.

Bài tập 2: Trong hệ trục tọa độ (O; $\overrightarrow{i}$ ; $\overrightarrow{j}$ ), Cho hình thoi ABCD tâm O có $AC = 8,\ \ BD = 6$ . Biết $\overrightarrow{OC}$ và $\overrightarrow{i}$ cùng hướng, $\overrightarrow{OB}$ và $\overrightarrow{j}$ cùng hướng.

a) Tính tọa độ các đỉnh của hình thoi.

b) Tìm tọa độ trung điểm I của BC và trọng tâm tam giác ABC.

Bài tập 3: Cho ba điểm A(-4; 0), B(0; 3) và C(2; 1)

a) Xác định tọa độ vectơ $\overrightarrow{u} = 2\overrightarrow{AB} - \overrightarrow{AC}$ .

b) Tìm điểm M sao cho $\overrightarrow{MA} + 2\overrightarrow{MB} + 3\overrightarrow{MC} = \overrightarrow{0}$ .

Bài tập 4: Cho tam giác có .

a) Tìm tọa độ trung điểm M sao cho C là trung điểm của đoạn MB.

b) Xác định trọng tâm tam giác .

b) Tìm điểm D sao cho là hình bình hành.

Bài tập 5. Trong mặt phẳng tọa độ Oxy, cho A(-2; 3) ; B(4; 5); C(2; -3)

a. Chứng minh ba điểm A, B, C không thẳng hàng.

b. Tìm tọa độ trọng tâm G của tam giác ABC.

c. Giải tam giác ABC (làm tròn các kết quả đến hàng đơn vị).

Bài tập 6: Trong mặt phẳng tọa độ cho $A(3; - 1),\ \ B( - 1;2)$ và . Xác định tọa độ các điểm C, D sao cho tứ giác là hình bình hành biết I là trọng tâm tam giác . Tìm tọa tâm O của hình bình hành .

Bài tập 7: Cho tam giác có $A(3;1),\ \ B(1; - 3)$ , đỉnh C nằm trên và trọng tâm G nằm trên trục . Tìm tọa độ đỉnh C

Bài tập 8. Cho tam giác có $M,\ \ N,\ \ P$ lần lượt là trung điểm của $BC,\ \ CA,\ \ AB$ . Biết . Tìm tọa độ các đỉnh của tam giác .

D. Đáp án bài tập tự rèn luyện

Bài tập 1.

a) Ta có: $A\left( 0;\frac{a\sqrt{3}}{2} \right),\ \ B\left( - \frac{a}{2};0 \right),\ \ C\left( \frac{a}{2};0 \right)$

b) Ta có: $E\left( \frac{a}{4};\frac{a\sqrt{3}}{4} \right)$

c) Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm $G\left( 0;\frac{a\sqrt{3}}{6} \right)$ .

Bài tập 2.

a) $A( - 4;0),\ \ C(4;0),\ \ B(0;3),\ \ D(0; - 3)$

b) $I\left( 2;\frac{3}{2} \right),\ \ G(0;1)$

Bài tập 3

a) Ta có $\overrightarrow{AB}(4;3),\ \ \overrightarrow{AC}(6;1)$ suy ra $\overrightarrow{u} = (2;5)$

b) Gọi , ta có $\overrightarrow{MA}( - 4 - x; - y),\ \ \overrightarrow{MB}( - x;3 - y),\ \ \overrightarrow{MC}(2 - x;1 - y)$

Suy ra $\overrightarrow{MA} + 2\overrightarrow{MB} + 3\overrightarrow{MC} = ( - 6x + 2; - 6y + 9)$

Do đó $\overrightarrow{MA} + 2\overrightarrow{MB} + 3\overrightarrow{MC} = \overrightarrow{0}$

$\Rightarrow \left\{ \begin{matrix} - 6x + 2 = 0 \\ - 6y + 9 = 0 \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = \frac{1}{3} \\ y = \frac{3}{2} \end{matrix} \right.$

Vậy $M\left( \frac{1}{3};\frac{3}{2} \right)$

🔍 Để thuận tiện cho việc học tập và lưu trữ, mời bạn tải tài liệu tham khảo bên dưới.

-------------------------------------------------------

Gợi ý tài liệu tham khảo:

Qua bài viết “Cách tìm tọa độ điểm, tọa độ vectơ trong mặt phẳng Oxy”, bạn đã được hệ thống lại toàn bộ lý thuyết, công thức và phương pháp tìm tọa độ một cách dễ hiểu và đầy đủ. Hãy luyện tập thường xuyên với bài tập có đáp án chi tiết để củng cố kỹ năng và ghi nhớ lâu dài. Đừng quên theo dõi các chuyên đề tiếp theo để nâng cao khả năng giải toán vectơ – tọa độ Oxy Toán 10 một cách toàn diện và hiệu quả nhất.

Tải về

Chọn file muốn tải về: