VnDoc.com

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 Đề số 1

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 - Có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Dạng tài liệu: Đề thi

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 - Đề 1

Đề thi khảo sát chất lượng đầu năm lớp 10
Đáp án Đề thi khảo sát chất lượng đầu năm

Bước vào năm học mới, việc kiểm tra đánh giá đầu năm đóng vai trò quan trọng nhằm xác định năng lực học sinh sau kỳ nghỉ hè và làm căn cứ xây dựng kế hoạch ôn tập phù hợp. Trong bài viết này, chúng tôi gửi đến bạn Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 - Đề số 1, được biên soạn sát chương trình, phù hợp với định hướng ra đề hiện hành. Đề thi có đầy đủ đáp án và lời giải chi tiết, giúp học sinh tự kiểm tra kiến thức, làm quen với cấu trúc đề và cải thiện kỹ năng giải bài. Nếu bạn đang tìm kiếm một tài liệu chất lượng để ôn tập đầu năm, đừng bỏ qua đề thi này!

Đề thi khảo sát chất lượng đầu năm lớp 10

Môn: Toán – Đề số 1

Thời gian: 90 phút

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

Câu 1: Cho biểu thức

$A=\left( \frac{x\sqrt{x}+1}{x-1}-\frac{x-1}{\sqrt{x}-1} \right):\left( \sqrt{x}+\frac{\sqrt{x}-4}{\sqrt{x}-1} \right)$ $A=\left( \frac{x\sqrt{x}+1}{x-1}-\frac{x-1}{\sqrt{x}-1} \right):\left( \sqrt{x}+\frac{\sqrt{x}-4}{\sqrt{x}-1} \right)$

a. Tìm điều kiện xác định của biểu thức.

b. Rút gọn biểu thức.

c. Tìm giá trị x nguyên để A nguyên.

Câu 2: Cho phương trình _{${{x}^{2}}-2mx+{{m}^{2}}+m-1=0$}

a. Giải phương trình khi _$m=1$.

b. Xác định m để phương trình có hai nghiệm phân biệt _{${{x}_{1}},{{x}_{2}}$}thỏa mãn điều kiện sau: _{$x_{1}^{2}+x_{2}^{2}+2{{x}_{1}}-3{{x}_{1}}{{x}_{2}}+2{{x}_{2}}=4$.}

Câu 3: Cho parabol _{$\left( P \right)=\frac{{{x}^{2}}}{2}$} và đường thẳng _{$\left( d \right):y=2x+3$}

a. Vẽ _{$\left( P \right)$} và d trên cùng hệ trục tọa độ.

b. Tìm tọa độ giao điểm của _{$\left( P \right)$} và d.

Câu 4: Cho nửa đường tròn đường kính _$AB=2R$. Từ A và B kẻ hai tiếp tuyến Ax và By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ 3 cắt các tiếp tuyến Ax, By lần lượt ở C, D. Các đường thẳng AD, BC cắt nhau tại N.

a. Chứng minh 4 điểm O, M, B, D cùng nằm trên một đường tròn, xác định tâm đường tròn đó.

b. Chứng minh: _{$\widehat{COD}={{90}^{0}}$.}

c. Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.

d. Xác định vị trí của P để ACDB đạt giá trị nhỏ nhất.

Câu 5: Cho 3 số thực dương thỏa mãn điều kiện _$xyz=1$. Chứng minh rằng:

$\frac{1}{{{x}^{2}}+{{y}^{2}}+1}+\frac{1}{{{y}^{2}}+{{z}^{2}}+1}+\frac{1}{{{z}^{2}}+{{x}^{2}}+1}\le 1$ $\frac{1}{{{x}^{2}}+{{y}^{2}}+1}+\frac{1}{{{y}^{2}}+{{z}^{2}}+1}+\frac{1}{{{z}^{2}}+{{x}^{2}}+1}\le 1$

Đáp án Đề thi khảo sát chất lượng đầu năm

Câu 1:

a. Điều kiện xác định: $\left\{ \begin{matrix} x - 1 \neq 0 \\ \sqrt{x} - 1 \neq 0 \\ x \geq 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \neq 1 \\ x \geq 0 \\ \end{matrix} \right.$ $\left\{ \begin{matrix} x - 1 \neq 0 \\ \sqrt{x} - 1 \neq 0 \\ x \geq 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \neq 1 \\ x \geq 0 \\ \end{matrix} \right.$

b. $A = \left( \frac{x\sqrt{x} + 1}{x - 1} - \frac{x - 1}{\sqrt{x} - 1} \right):\left( \sqrt{x} + \frac{\sqrt{x} - 4}{\sqrt{x} - 1} \right)$ $A = \left( \frac{x\sqrt{x} + 1}{x - 1} - \frac{x - 1}{\sqrt{x} - 1} \right):\left( \sqrt{x} + \frac{\sqrt{x} - 4}{\sqrt{x} - 1} \right)$

$A = \left( \frac{\left( \sqrt{x} + 1 \right)\left( x - \sqrt{x} + 1 \right)}{x - 1} - \frac{\left( \sqrt{x} + 1 \right)\left( \sqrt{x} - 1 \right)}{\sqrt{x} - 1} \right):\left( \frac{\sqrt{x}\left( \sqrt{x} - 1 \right) + \sqrt{x} - 4}{\sqrt{x} - 1} \right)$ $A = \left( \frac{\left( \sqrt{x} + 1 \right)\left( x - \sqrt{x} + 1 \right)}{x - 1} - \frac{\left( \sqrt{x} + 1 \right)\left( \sqrt{x} - 1 \right)}{\sqrt{x} - 1} \right):\left( \frac{\sqrt{x}\left( \sqrt{x} - 1 \right) + \sqrt{x} - 4}{\sqrt{x} - 1} \right)$

$A = \left\lbrack \frac{x - \sqrt{x} + 1}{\sqrt{x} - 1} - (\sqrt{x} + 1) \right\rbrack:\left( \frac{x - 4}{\sqrt{x} - 1} \right)$ $A = \left\lbrack \frac{x - \sqrt{x} + 1}{\sqrt{x} - 1} - (\sqrt{x} + 1) \right\rbrack:\left( \frac{x - 4}{\sqrt{x} - 1} \right)$

$A = \left\lbrack \frac{x - \sqrt{x} + 1 - x + 1}{\sqrt{x} - 1} \right\rbrack.\frac{\sqrt{x} - 1}{x - 4}$ $A = \left\lbrack \frac{x - \sqrt{x} + 1 - x + 1}{\sqrt{x} - 1} \right\rbrack.\frac{\sqrt{x} - 1}{x - 4}$

$A = \frac{- \sqrt{x} + 2}{\sqrt{x} - 1}.\frac{\sqrt{x} - 1}{x - 4} = \frac{- 1}{\sqrt{x} + 2}$ $A = \frac{- \sqrt{x} + 2}{\sqrt{x} - 1}.\frac{\sqrt{x} - 1}{x - 4} = \frac{- 1}{\sqrt{x} + 2}$

c. Để A đạt giá trị nguyên thì $\sqrt{x} + 2 \in U(1)^{+} = \left\{ 1 \right\}$ $\sqrt{x} + 2 \in U(1)^{+} = \left\{ 1 \right\}$

$\Rightarrow \sqrt{x} + 2 \geq 2 > 1$ $\Rightarrow \sqrt{x} + 2 \geq 2 > 1$

$\Rightarrow$ $\Rightarrow$không có giá trị x nguyên nào để A đạt giá trị nguyên

Câu 2:

a. Thay $m = 1$ vào phương trình ta có:

$x^{2} - 2x + 1 = 0 \Leftrightarrow (x - 1)^{2} = 0 \Leftrightarrow x = 1$ $x^{2} - 2x + 1 = 0 \Leftrightarrow (x - 1)^{2} = 0 \Leftrightarrow x = 1$

Kết luận với $m = 1$ thì phương trình có nghiệm $x = 1$

b. Để phương trình có 2 nghiệm phân biệt $x_{1},x_{2}$ $x_{1},x_{2}$thì:

$\begin{matrix} \Delta$ $\begin{matrix} \Delta' > 0 \\ \Delta' = m^{2} - m^{2} - m + 1 = 1 - m > 0 \Rightarrow m < 1 \\ \end{matrix}$

Áp dụng hệ thức Vi – et ta có: $\left\{\begin{matrix}x_{1} + x_{2} = - \dfrac{b}{a} = 2m \\x_{1}.x_{2} = \dfrac{c}{a} = m^{2} + m - 1 \\\end{matrix} \right.$ $\left\{\begin{matrix}x_{1} + x_{2} = - \dfrac{b}{a} = 2m \\x_{1}.x_{2} = \dfrac{c}{a} = m^{2} + m - 1 \\\end{matrix} \right.$

$\begin{matrix} x_1^2 + x_2^2 + 2{x_1} - 3{x_1}{x_2} + 2{x_2} = 4 \hfill \\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 5{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) = 4 \hfill \\ \Leftrightarrow {\left( {2m} \right)^2} - 5\left( {{m^2} + m - 1} \right) + 4m = 4 \hfill \\ \Leftrightarrow - {m^2} - m + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {m = \dfrac{{ - 1 + \sqrt 5 }}{2}} \\ {m = \dfrac{{ - 1 - \sqrt 5 }}{2}} \end{array}} \right.\left( {Tm} \right) \hfill \\ \end{matrix}$ $\begin{matrix} x_1^2 + x_2^2 + 2{x_1} - 3{x_1}{x_2} + 2{x_2} = 4 \hfill \\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 5{x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) = 4 \hfill \\ \Leftrightarrow {\left( {2m} \right)^2} - 5\left( {{m^2} + m - 1} \right) + 4m = 4 \hfill \\ \Leftrightarrow - {m^2} - m + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {m = \dfrac{{ - 1 + \sqrt 5 }}{2}} \\ {m = \dfrac{{ - 1 - \sqrt 5 }}{2}} \end{array}} \right.\left( {Tm} \right) \hfill \\ \end{matrix}$

Vậy $m = \frac{- 1 \pm \sqrt{5}}{2}$ $m = \frac{- 1 \pm \sqrt{5}}{2}$thì phương trình có 2 nghiệm phân biệt thỏa mãn: $x_{1}^{2} + x_{2}^{2} + 2x_{1} - 3x_{1}x_{2} + 2x_{2} = 4$ $x_{1}^{2} + x_{2}^{2} + 2x_{1} - 3x_{1}x_{2} + 2x_{2} = 4$

Câu 3:

a. Học sinh tự vẽ

b. Phương trình hoành độ giao điểm là:

$\frac{x^{2}}{2} = 2x + 3 \Leftrightarrow x^{2} - 4x - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 2 + \sqrt{10} \\ x = 2 - \sqrt{10} \\ \end{matrix} \right.$ $\frac{x^{2}}{2} = 2x + 3 \Leftrightarrow x^{2} - 4x - 6 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 2 + \sqrt{10} \\ x = 2 - \sqrt{10} \\ \end{matrix} \right.$

Vậy tọa độ gia điểm của (P) và d là: $A\left( 2 + \sqrt{10},7 + 2\sqrt{10} \right),B\left( 2 - \sqrt{10},7 - 2\sqrt{10} \right)$ $A\left( 2 + \sqrt{10},7 + 2\sqrt{10} \right),B\left( 2 - \sqrt{10},7 - 2\sqrt{10} \right)$

Câu 4:

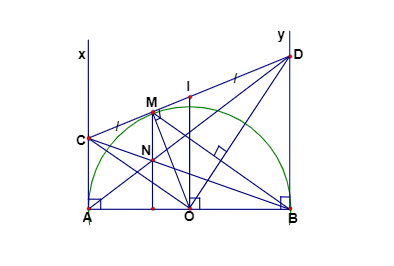
Chứng minh

a. Xét tứ giác OMBD có: $\widehat{OMD} + \widehat{OBD} = 180^{0} \Rightarrow$ $\widehat{OMD} + \widehat{OBD} = 180^{0} \Rightarrow$Tứ giác OMBD nội tiếp đường tròn tâm là trung điểm của OD và bán kính $\frac{OD}{2}$ $\frac{OD}{2}$

b. Ta có: OC là phân giác góc $\widehat{AOM}$ $\widehat{AOM}$, OD là phân giác góc $\widehat{MOB}$ $\widehat{MOB}$

Mặt khác $\widehat{AOM} + \widehat{MOB} = 180^{0} \Rightarrow \widehat{COD} = 90^{0}$ $\widehat{AOM} + \widehat{MOB} = 180^{0} \Rightarrow \widehat{COD} = 90^{0}$

c. Gọi I là trung điểm của CD

I là tâm đường tròn ngoại tiếp tam giác COD, IO là bán kính

Theo tính chất tiếp tuyến ta có: $AC\bot AB,BD\bot AB \Rightarrow BD//AC$ $AC\bot AB,BD\bot AB \Rightarrow BD//AC$. Vậy ACDB là hình thang

Ta lại có I là trung điểm của CD, O là trung điểm AB. Vậy OI là đường trung bình của hình thang ACDB

$\Rightarrow$ $\Rightarrow$IO // AC, mà $AC\bot AB \Rightarrow IO\bot AB$ $AC\bot AB \Rightarrow IO\bot AB$ tại O. Vậy AB là tiếp tuyến tại O của đường tròn đường kính CD

d. Ta có chu vi tứ giác ACDB = AB + AC + CD + BD mà AC + BD = CD nên chu vi ACBD = AB + 2CD mà AB không đổi nên chu vi tứ giác ACDB nhỏ nhất khi CD CD là khoảng cách giữa Ax và By tức là CD vuông góc với Ax và By. Khi đó CD//AB. Vậy M là trung điểm của AB

Mời bạn đọc tải tài liệu để xem lời giải hướng dẫn chi tiết !

---------------------------------------------

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 Đề số 1 là tài liệu hữu ích giúp học sinh tự đánh giá năng lực, hệ thống lại kiến thức cơ bản từ lớp 9 và làm quen với phong cách ra đề ở bậc THPT. Việc luyện đề thường xuyên sẽ giúp các em rèn luyện kỹ năng tính toán, trình bày bài thi và làm quen với thời gian làm bài thực tế. Ngoài ra, đáp án chi tiết đi kèm sẽ hỗ trợ các em tự học hiệu quả tại nhà mà không cần quá phụ thuộc vào giáo viên. Đừng quên theo dõi các đề thi tiếp theo thuộc bộ Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 - Có đáp án để có sự chuẩn bị toàn diện và tự tin bước vào năm học mới!

Tải về

Chọn file muốn tải về: