Đề thi chọn lớp khối 10 môn Toán trường THPT Yên Lạc 2, Vĩnh Phúc năm học 2016 - 2017

Đề thi chọn lớp khối 10 môn Toán

Đề thi chọn lớp khối 10 môn Toán trường THPT Yên Lạc 2, Vĩnh Phúc năm học 2016 - 2017 là đề kiểm tra khảo sát khối 10, nhằm phân loại chất lượng học sinh, từ đó xếp vào các lớp thích hợp để có phương pháp dạy học phù hợp với các em. Mời quý thầy cô và các em cùng tham khảo.

Đề thi chọn lớp khối 10 môn Ngữ văn trường THPT Yên Lạc 2, Vĩnh Phúc năm học 2016 - 2017

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 trường THPT Nguyễn Văn Cừ, Bắc Ninh năm học 2014 - 2015

Câu 1 (1,5 điểm).

1. Không sử dụng máy tính cầm tay hãy giải hệ phương trình:
2. Tìm m để hàm số y = (m - 1)x + 2m + 1 đồng biến trên R.

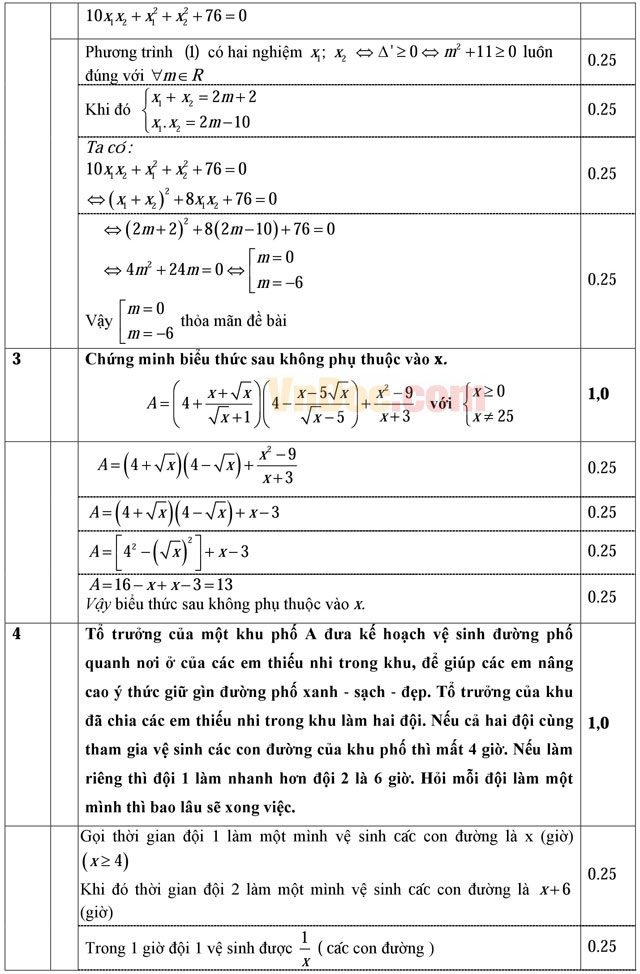
Câu 2 (2,0 điểm). Cho phương trình x² - 2(1 + m)x + 2m - 10 = 0 (1)

1. Giải phương trình (1) với m = 1.
2. Tìm m để phương trình (1) có hai nghiệm x₁, x₂; sao cho 10x₁x₂ + x₁² + x₂² + 76 = 0.

Câu 3 (1,0 điểm). Chứng minh biểu thức sau không phụ thuộc vào x.

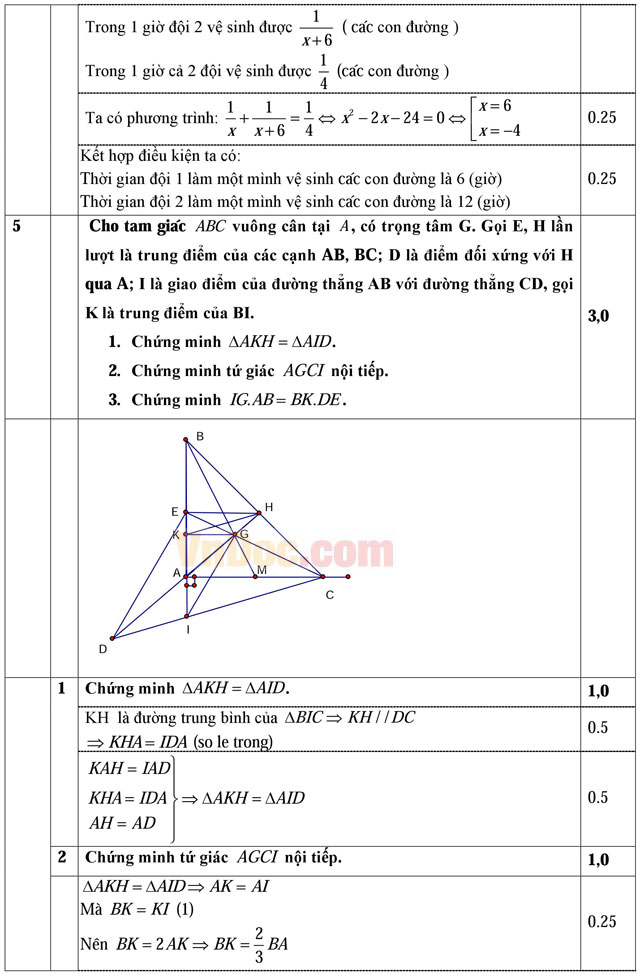
Câu 4 (1,0 điểm). Tổ trưởng của một khu phố A đưa kế hoạch vệ sinh đường phố quanh nơi ở của các em thiếu nhi trong khu, để giúp các em nâng cao ý thức giữ gìn đường phố xanh - sạch - đẹp. Tổ trưởng của khu đã chia các em thiếu nhi trong khu làm hai đội. Nếu cả hai đội cùng tham gia vệ sinh các con đường của khu phố thì mất 4 giờ. Nếu làm riêng thì đội 1 làm nhanh hơn đội 2 là 6 giờ. Hỏi mỗi đội làm một mình thì bao lâu sẽ xong việc.

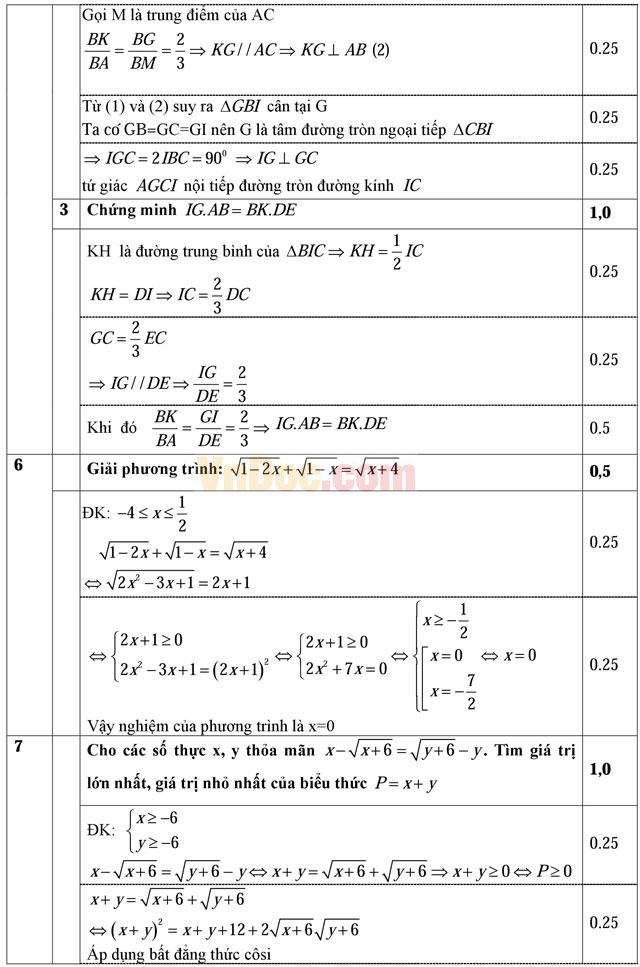
Câu 5 (3,0 điểm). Cho tam giác ABC vuông cân tại A, có trọng tâm G. Gọi E, H lần lượt là trung điểm của các cạnh AB, BC; D là điểm đối xứng với H qua A; I là giao điểm của đường thẳng AB với đường thẳng CD, gọi K là trung điểm của BI.

1. Chứng minh ΔAKH = ΔAID.
2. Chứng minh tứ giác AGCI nội tiếp.
3. Chứng minh IG.AB = BK.DE.

Câu 6 (0,5 điểm). Giải phương trình:

Câu 7 (1,0 điểm). Cho hai số thực x, y thỏa mãn . Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = x + y.

Đáp án đề thi chọn lớp khối 10 môn Toán