VnDoc.com

Đề cương ôn tập học kì 2 môn Toán lớp 10

Nội dung ôn tập thi học kỳ II lớp 10 môn Toán

Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí

Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188

ĐỀ CƯƠNG ÔN TẬP HỌC KÌ II MÔN TOÁN 10

(Tài liệu lưu hành nội bộ)

------------- Biên soạn: Trần Hải Nam ----------------

A. CÁC VẤN ĐỀ TRONG HỌC KÌ II

I. Đại số:

1. Xét dấu nhị thức, tam thức bậc hai; Giải phương trình, bất phương trình qui về bậc nhất; bậc

hai; phương trình có chứa căn, trị tuyệt đố, tìm điều kiện phương trình, bất phương trình có

nghiệm, vô nghiệm, có nghiệm thỏa mãn điều kiện.

2. Giải hệ bất phương trình bậc hai.

3. Biễu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn; ứng dụng vào bài toán tối ưu.

4. Tính tần số; tần suất các đặc trưng mẫu; vẽ biểu đồ biễu diễn tần số, tần suất (chủ yếu hình cột

và đường gấp khúc).

5. Tính số trung bình, số trung vị, mốt, phương sai và độ lệch chuẩn của số liệu thống kê.

6. Tính giá trị lượng giác một cung, một biểu thức lượng giác.

7. Vận dụng các công thức lượng giác vào bài toán rút gọn hay chứng minh các đẳng thức lượng

giác.

II. Hình học:

1. Viết phương trình đường thẳng (tham số,tổng quát, chính tắc)

2. Xét vị trí tương đối điểm và đường thẳng;đường thẳng và đường thẳng

3. Tính góc giữa hai đường thẳng; khoảng cách từ điểm đến đường thẳng.

4. Viết phương trình đường phân giác (trong và ngoài).

5. Viết phương trình đường tròn; Xác định các yếu tố hình học của đường tròn.viết phương trình

tiếp tuyến của đường tròn; biết tiếp tuyến đi qua một điểm (trên hay ngoài đường tròn), song

song, vuông góc một đường thẳng.

6. Viết phương trình chính tắc của elíp; xác định các yếu tố của elíp.

7. Viết phương trình chính tắc của hypebol; xác định các yếu tố của hypebol.

8. Viết phương trình chính tắc của parabol; xác định các yếu tố của parabol.

9. Ba đường cô níc: khái niệm đường chuẩn, tính chất chung của ba đường coníc.

B. CƠ SỞ LÝ THUYẾT

I. Phần Đại số

1. Bất phương trình và hệ bất phương trình

퍸่  iến đổi ất ương tn

a h〹p cng:  䁞 䁞c nh trn

D

th 䁞  䁞



䁞 + 䁞  䁞 + 䁞

 h〹p nhn:

Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí

Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188

  䁞  0,



䁞



D

th 䁞  䁞



䁞.䁞  䁞.䁞

  䁞  0,



䁞



D th 䁞  䁞



䁞.䁞  䁞.䁞

c h〹p nh phng:  䁞



0 v 䁞



0,



䁞



D th 䁞  䁞



2 2

   P x Q x

2. Dấu của nhị thức bậc nhất

Dấu nhị thức bậc nhất f(x) = ax + 

x

–



b

a



+



f(x)

Tri dấ với hệ số a 0 Cùng dấ với hệ số a

 o  ới a  0 ta c:

   f x a a f x a    

 

f x a

 



 







3. Phương trình và hệ bất phương trình bậc nhất hai ẩn

a. i din hnh hⲨc tp nghiệm của ất phng trnh a䁞 + 

c

1 

2 2

a b

0



Bước 1: Trong mp 䁞, v ng thng 



: ax + by

c

Bước 2: ấ

 ;   

o o o

M x y  

thng lấ

o

M O



Bước 3: Tnh a䁞

o

+ 

o

v so snh a䁞

o

+ 

o

v c.

Bước 4: t ln

  a䁞

o

+ 

o

 c th na mp  



 cha 

o

l min nghiệm của ax + by

c



 a䁞

o

+ 

o

 c th na mp  



 hng cha 

o

l min nghiệm của ax + by

c

.   min nghiệm của pt 1 ta ợc min nghiệm của pt a䁞 + b  c. in nghiệm của

cc pt ax + by

c

v ax + by

c

ợc 䁞c nh tng t.

่. i din hnh hⲨc tp nghiệm của hệ ất phng trnh c nhất 2 n:



ới mỗi ất phng trnh trong hệ, ta 䁞c nh min nghiệm của n v gch  min cn li.



a hi lm nh trn ln lợt ối với tất c cc pt trong hệ trn cùng mt mp tⲨa , min

cn li hng  gch chnh l min nghiệm của hệ pt  cho.

4. Dấu của tam thức bậc hai

a. Địn lí về dấu ่ủa tam tứ่ ậ่ ai

Địn lí 䁞 = a䁞

2

+ 䁞 + c, a



0

 c mt số



sao cho

 

. 0a f





th:

- 䁞=0 c hai nghiệm phn iệt 䁞

1

v 䁞

2

- ố



nằm giữa 2 nghiệm

1 2

x x



 

Hệ quả 1:

Cho tam thc c hai 䁞 = a䁞

2

+ 䁞 + c, a



0,



= 

2

– 4ac

 



 0 th 䁞 cùng dấ với hệ số a a..䁞0,



䁞



R

Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí

Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188

 



= 0 th 䁞 cùng dấ với hệ số a a..䁞0,



䁞



2

b

a



 



 0 th 䁞 cùng dấ với hệ số a hi 䁞  䁞

1

hoặc 䁞  䁞

2

; 䁞 tri dấ với hệ số a hi 䁞

1

 䁞  䁞

2

. ới 䁞

1

, 䁞

2

l hai nghiệm của 䁞 v 䁞

1

 䁞

2



Bảng xét dấu: 䁞 = a䁞

2

+ 䁞 + c, a



0,



= 

2

– 4ac  0

x

–



x

1

x

2

+



f(x)

(Cùng dấu với hệ số a) 0 (Trái dấu với hệ số a) 0 (Cùng dấu với hệ số a)

Hệ quả 2

+

 

1 2

. 0x x a f

 

   

+

 

1 2

. 0

0

2

a f

x x

S











    









+

 

1 2

. 0

0

2

a f

x x

S











    









+

 

 

1 2

. 0

,

0

a f

x x









 



 





Hệ quả 3

+

 

1 2

. 0

a f

x x

a f



 









   









+

 

1 2

. 0

a f

x x

a f



 









   









+

 

1 2

. 0

a f

x x

a f



 









   









+

   

1 2

. 0

x x

f f

x x

 

  



 



  





1

x



2

x

2

S





2

S





2

S





Đề cương ôn tập học kì 2 môn Toán lớp 10 giúp các bạn học sinh ôn tập lý thuyết và các dạng bài tập cơ bản về đại số và hình học trong chương trình Toán 10, từ đó sẵn sàng cho bài kiểm tra giữa học kì II, bài kiểm tra cuối năm sắp tới. Chúc các bạn học tốt. Mời các bạn cùng tham khảo chi tiết và tải về bài viết dưới đây nhé.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 10, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 10 sau: Nhóm Tài liệu học tập lớp 10. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đề cương ôn tập môn Hóa học lớp 10 học kì 2
Đề cương ôn tập học kì 2 môn Sinh học lớp 10
Bộ đề thi học kì 2 môn Toán lớp 10 - Có đáp án
Bài tập môn Toán lớp 10 trường THPT Trần Đại Nghĩa năm 2020

ĐỀ CƯƠNG ÔN TẬP HỌC KÌ II MÔN TOÁN 10

A. CÁC VẤN ĐỀ TRONG HỌC KÌ II

I. Đại số:

Xét dấu nhị thức, tam thức bậc hai; Giải phương trình, bất phương trình qui về bậc nhất, bậc hai; phương trình có chứa căn, trị tuyệt đối, tìm điều kiện phương trình, bất phương trình có nghiệm, vô nghiệm, có nghiệm thỏa mãn điều kiện.
Giải hệ bất phương trình bậc hai.
Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn; ứng dụng vào bài toán tối ưu.
Tính tần số; tần suất các đặc trưng mẫu; vẽ biểu đồ biễu diễn tần số, tần suất (chủ yếu hình cột và đường gấp khúc).
Tính số trung bình, số trung vị, mốt, phương sai và độ lệch chuẩn của số liệu thống kê.
Tính giá trị lượng giác một cung, một biểu thức lượng giác.
Vận dụng các công thức lượng giác vào bài toán rút gọn hay chứng minh các đẳng thức lượng giác.
Tìm tham số m thỏa điều kiện cho trước: PT có hai nghiệm phân biệt, hai nghiệm trái dấu, hai nghiệm cùng dương, hai nghiệm cùng âm; tam thức bậc hai luôn dương, luôn âm; bất phương trình vô nghiệm,…

II. Hình học:

Viết phương trình đường thẳng (tham số, tổng quát, chính tắc)
Xét vị trí tương đối điểm và đường thẳng; đường thẳng và đường thẳng
Tính góc giữa hai đường thẳng; khoảng cách từ điểm đến đường thẳng.
Viết phương trình đường phân giác (trong và ngoài).
Viết phương trình đường tròn; Xác định các yếu tố hình học của đường tròn. Viết phương trình tiếp tuyến của đường tròn; biết tiếp tuyến đi qua một điểm (trên hay ngoài đường tròn), song song, vuông góc một đường thẳng.
Viết phương trình chính tắc của hypebol; xác định các yếu tố của hypebol.
Viết phương trình chính tắc của parabol; xác định các yếu tố của parabol.
Ba đường cô níc: khái niệm đường chuẩn, tính chất chung của ba đường cô níc.

B. CƠ SỞ LÝ THUYẾT

I. Phần Đại số

1. Bất phương trình và hệ bất phương trình

Các phép biến đổi bất phương trình:

a) Phép cộng: Nếu f(x) xác định trên D thì P(x) < Q(x) ↔ P(x) + f(x) < Q(x) + f(x)

b) Phép nhân:

Nếu f(x) > 0, ∀ x ∈ D thì P(x) < Q(x) ↔ P(x).f(x) < Q(x).f(x)
Nếu f(x) < 0, ∀ x ∈ D thì P(x) < Q(x) ↔ P(x).f(x) > Q(x).f(x)

c) Phép bình phương: Nếu P(x) ≥ 0 và Q(x) ≥ 0, ∀ x ∈ D thì P(x) < Q(x) ↔ P²(x) < Q²(x)

2. Dấu của nhị thức bậc nhất

Dấu nhị thức bậc nhất f(x) = ax + b

x	–∞ -b/a +
f(x)	(Trái dấu với hệ số a) 0 (Cùng dấu với hệ số a)

* Chú ý: Với a > 0 ta có:

Đề cương ôn tập học kì 2 môn Toán lớp 10

3. Phương trình và hệ bất phương trình bậc nhất hai ẩn

a. Biểu diễn hình học tập nghiệm của bất phương trình ax + by ≤ c (1) (a² + b² ≠ 0)

Bước 1: Trong mp Oxy, vẽ đường thẳng (Δ): ax + by = c

Bước 2: Lấy M_o(x_o; y_o) ∉ (Δ) (thường lấy M_o ≡ 0)

Bước 3: Tính ax_o + by_o và so sánh ax_o + by_o và c.

Bước 4: Kết luận

Nếu ax_o + by_o < c thì nửa mp bờ (Δ) chứa M_o là miền nghiệm của ax + by

Nếu ax_o + by_o > c thì nửa mp bờ (Δ) không chứa M_o là miền nghiệm của ax + by

b. Bỏ bờ miền nghiệm của bpt (1) ta được miền nghiệm của bpt ax + by < c. Miền nghiệm của các bpt ax + by ≥ 0 và ax + by > c được xác định tương tự.

c. Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất 2 ẩn:

Với mỗi bất phương trình trong hệ, ta xác định miền nghiệm của nó và gạch bỏ miền còn lại.
Sau khi làm như trên lần lượt đối với tất cả các bpt trong hệ trên cùng một mp tọa độ, miền còn lại không bị gạch chính là miền nghiệm của hệ bpt đã cho.

4. Dấu của tam thức bậc hai

a. Định lí về dấu của tam thức bậc hai:

Định lí: f(x) = ax² + bx + c, a ≠ 0

Nếu có một số α sao cho a.f(α) < 0 thì:

f(x) = 0 có hai nghiệm phân biệt x₁ và x₂
Số α nằm giữa 2 nghiệm x₁ < α < x₂

Hệ quả 1:

Cho tam thức bậc hai f(x) = ax² + bx + c, a ≠ 0, Δ = b² – 4ac

Nếu Δ < 0 thì f(x) cùng dấu với hệ số a (a..f(x) > 0), ∀ x ∈ R
Nếu Δ = 0 thì f(x) cùng dấu với hệ số a (a..f(x) > 0), ∀ x ≠ -b/2a
Nếu Δ > 0 thì f(x) cùng dấu với hệ số a khi x < x₁ hoặc x > x₂; f(x) trái dấu với hệ số a khi x₁ < x < x₂. (Với x₁, x₂ là hai nghiệm của f(x) và x₁ < x₂)

Bảng xét dấu: f(x) = ax² + bx + c, a ≠ 0, Δ = b² – 4ac > 0

x	–∞ x₁ x₂ +∞
f(x)	(Cùng dấu với hệ số a) 0 (Trái dấu với hệ số a) 0 (Cùng dấu với hệ số a)

Hệ quả 2:

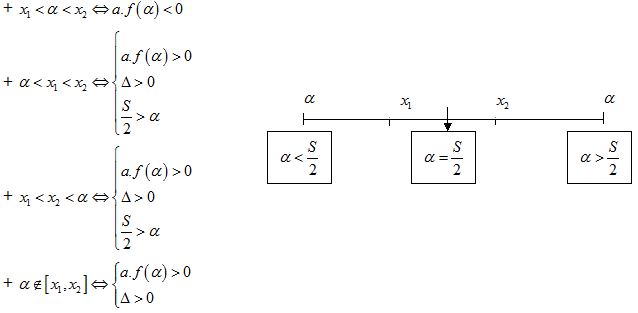
Hệ quả 3:

b. Dấu của nghiệm số

Cho f(x) = ax² + bx + c, a≠0

a, ax² + bx + c, a≠0 có nghiệm <=> Δ = b² - 4ac ≥ 0

b, ax² + bx + c, a≠0 có 2 nghiệm trái dấu <=> a,c < 0

c, ax² + bx + c, a≠0 có 2 nghiệm cùng dấu: Δ >0 và a,c > 0

d, ax² + bx + c, a≠0 có các nghiệm dương Δ ≥ 0, P = x₁x₂ = c/a >0, S = x₁ + x₂ = -b/a>0

e, ax² + bx + c, a≠0 có các nghiệm âm: Δ ≥ 0, P = x₁x₂ = c/a >0, S = x₁ + x₂ = -b/a>0

Chú ý: Dấu của tam thức bậc hai luôn luôn cùng dấu với hệ số a khi Δ < 0

5. Bất phương trình bậc hai

a, Định nghĩa:

Bất phương trình bậc hai là bpt có dạng f(x) > 0 hoặc f(x) ≥ 0, f(x) < 0, f(x) ≤ 0 trong đó f(x) là một tam thức bậc hai: f(x) = ax² + bx + c, a≠0

b, Cách giải:

Để giải bất phương trình bậc hai, ta áp dụng định lý và dấu tam thức bậc hai

Bước 1: Đặt vế trái bằng f(x), rồi xét dấu f(x)

Bước 2: Dựa vào bảng xét dấu và chiều của bpt để kết luận nghiệm của bpt

6. Thống kê

Kiến thức cần nhớ:

Bảng phân bố tần suất
Biểu đồ
Số trung bình cộng, số trung vị, mốt
Phương sai độ lệch chuẩn

7. Lượng giác

Trên đây VnDoc đã chia sẻ đến các bạn học sinh Đề cương ôn tập học kì 2 môn Toán lớp 10 trong thời gian nghỉ dịch viêm phổi cấp. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài học rồi đúng không ạ? Bài viết cho chúng ta thấy được nội dung đề cương ôn tập học kì 2 môn Toán lớp 10 về cả phần đại số và hình học. Bên cạnh đó VnDoc.com còn tổng hợp các bài tập luyện tập kèm theo giúp các bạn luyện tập kiến thức của mình. Hy vọng với tài liệu này các bạn học sinh sẽ theo kịp chương trình lớp 10, đồng thời nắm chắc kiến thức, ngoài ra các bạn tham khảo thêm lịch học trực tuyến trên truyền hình lớp 10, chương trình học trực tuyến trên truyền hình Hà Nội

.........................................

Ngoài Đề cương ôn tập học kì 2 môn Toán lớp 10. Để giúp bạn đọc có thêm nhiều tài liệu học tập hơn nữa, VnDoc.com mời các bạn học sinh còn có thể tham khảo thêm tài liệu học tập các đề thi học kì 1 lớp 10, đề thi học kì 2 lớp 10 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với tài liệu lớp 10 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Để giúp bạn đọc có thể giải đáp được những thắc mắc và trả lời được những câu hỏi khó trong quá trình học tập. VnDoc.com mời bạn đọc cùng đặt câu hỏi tại mục hỏi đáp học tập của VnDoc. Chúng tôi sẽ hỗ trợ trả lời giải đáp thắc mắc của các bạn trong thời gian sớm nhất có thể nhé.