Giải bài tập trang 79 SGK Đại số 10: Bất đẳng thức

Giải bài tập môn Toán lớp 10

Giải bài tập trang 79 SGK Đại số 10: Bất đẳng thức

Giải bài tập trang 79 SGK Đại số 10: Bất đẳng thức hướng dẫn giải chi tiết các bài tập trong sách giáo khoa, hi vọng sẽ giúp các em học tốt môn Toán lớp 10. Mời các em cùng tham khảo.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 10, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 10 sau: Nhóm Tài liệu học tập lớp 10. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Giải bài 1, 2, 3, 4, 5, 6 trang 79 SGK Đại số 10: Bất đẳng thức

Bài 1 trang 79 SGK Đại số lớp 10: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x?

a) 8x > 4x	b) 4x > 8x
c) 8x² > 4x²	d) 8 + x > 4 + x

Hướng dẫn giải

- Tính chất liên hệ với phép cộng:

Với các số thực a, b, m bất kì ta luôn có:

$a\le b\Leftrightarrow a\pm m\le b\pm m$ $a\le b\Leftrightarrow a\pm m\le b\pm m$

Với các số thực a, b, c, d bất kì ta luôn có

$a\le b,c\le d\Rightarrow a+c\le b+d$ $a\le b,c\le d\Rightarrow a+c\le b+d$

$a\le b,c\le d\Rightarrow a-d\le b-c$ $a\le b,c\le d\Rightarrow a-d\le b-c$

- Tính chất liên hệ với phép nhân

Với các số thực a, b, c, d bất kì ta có: $\left\{ \begin{matrix} 0< a< b \\ 0< c< d \\ \end{matrix}\Rightarrow 0< a.c< b.d \right.$ $\left\{ \begin{matrix} 0< a< b \\ 0< c< d \\ \end{matrix}\Rightarrow 0< a.c< b.d \right.$

Đáp án và hướng dẫn giải bài 1:

a) Nếu x < 0 thì a) sai;

b) Nếu x > 0 thì b) sai;

c) Nếu x = 0 thì c) sai;

d) Đúng với mọi giá trị của x.

Bài 2 trang 79 SGK Đại số lớp 10: Cho số x > 5, số nào trong các số sau đây là nhỏ nhất?

$A=\frac{5}{x}$ $A=\frac{5}{x}$	$B=\frac{5}{x}+1$ $B=\frac{5}{x}+1$
$C=\frac{5}{x}-1$ $C=\frac{5}{x}-1$	$D=\frac{x}{5}$ $D=\frac{x}{5}$

Hướng dẫn giải

Tính chất cộng một số bất kì: $a< b\Rightarrow a+m< b+m$ $a< b\Rightarrow a+m< b+m$
Với mọi số m > 0 ta có: $a< b\Rightarrow a.m< b.m$ $a< b\Rightarrow a.m< b.m$
$0< a < b\Rightarrow {{a}^{2m}}< {{b}^{2m}},\forall m\in {{\mathbb{N}}^{*}}$ $0< a < b\Rightarrow {{a}^{2m}}< {{b}^{2m}},\forall m\in {{\mathbb{N}}^{*}}$

Đáp án và hướng dẫn giải bài 2:

Với x > 5 thì $0<\frac{5}{x}<1\Rightarrow \frac{5}{x}-1<0$ $0<\frac{5}{x}<1\Rightarrow \frac{5}{x}-1<0$

Trong khi đó $\frac{5}{x}>0,\frac{5}{x}+1>0,\frac{x}{5}>0$ $\frac{5}{x}>0,\frac{5}{x}+1>0,\frac{x}{5}>0$

Vậy với cùng số x > 5 thì biểu thức _{$C = \dfrac{5}{x} - 1$} có giá trị nhỏ nhất.

Bài 3 trang 79 SGK Đại số lớp 10: Cho a, b, c là độ dài ba cạnh của một tam giác.

a) Chứng minh (b - c)² < a²;

b) Từ đó suy ra a² + b² + c² < 2(ab + bc + ca).

Hướng dẫn giải

- Bất đẳng thức tam giác: _{$a+c > b,a+b >c$} (a, b, c là ba cạnh tam giác)

- Tính chất liên hệ với phép cộng:

Với các số thực a, b, m bất kì ta luôn có:

$a\le b\Leftrightarrow a\pm m\le b\pm m$ $a\le b\Leftrightarrow a\pm m\le b\pm m$

Với các số thực a, b, c, d bất kì ta luôn có

$a\le b,c\le d\Rightarrow a+c\le b+d$ $a\le b,c\le d\Rightarrow a+c\le b+d$

$a\le b,c\le d\Rightarrow a-d\le b-c$ $a\le b,c\le d\Rightarrow a-d\le b-c$

Đáp án và hướng dẫn giải bài 3:

a) Ta biết trong một tam giác thì một cạnh luôn nhỏ hơn tổng hai cạnh kia.

a + b > c => a + b – c > 0

a + c > b => a + c – b > 0

=> [a + (b + c)](a – (b – c)) > 0

=> a² – (b - c)² > 0 => a² > (b - c)².

b) Từ kết quả câu a), ta có:

a² + b² + c² > (b - c)² + (a – c)² + (a – b)²

<=> a² + b² + c² > b² + c² – 2bc + a2 + c² – 2ac + a² + b² – 2ab

<=> 2(ab + bc + ac) > a² + b² + c².

Bài 4 trang 79 SGK Đại số lớp 10: Chứng minh rằng:

x³ + y³ ≥ x²y + xy², ∀x ≥ 0, ∀y ≥ 0.

Hướng dẫn giải

- Chuyển vế bất đẳng thức đưa đa thức về dạng tích rồi đánh giá.

- Đa thức lũy thừa bậc chẵn luôn dương: _{${{a}^{2m}}\ge 0,\forall a,n\in {{\mathbb{N}}^{*}}$}

Đáp án và hướng dẫn giải bài 4:

Ta có: (x – y)² ≥ 0 <=> x² + y² – 2xy ≥ 0

<=> x² + y² – xy ≥ xy

Do x ≥ 0, y ≥ 0 => x + y ≥ 0,

Ta có (x + y)(x² + y² – xy) ≥ (x + y)xy <=> x³ + y³ ≥ x²y + xy².

Bài 5 trang 79 SGK Đại số lớp 10: Chứng minh rằng

x⁴ – √x⁵ + x – √x + 1 > 0, ∀x ≥ 0.

Hướng dẫn giải

Đặt ẩn phụ đơn giản biểu thức.

Đưa đa thức về dạng các đa thức nhỏ lũy thừa bậc chẵn rồi đánh giá đa thức.

Đáp án và hướng dẫn giải bài 5:

Đặt √x = t, x ≥ 0 => t ≥ 0.

Vế trái trở thành: t⁸ – t⁵ + t² – t + 1 = f(t)

Nếu t = 0, t = 1, f(t) = 1 >0

Với 0 < t <1, f(t) = t8 + (t² – t⁵) +1 – t

t⁸ > 0, 1 – t > 0, t² – t⁵ = t³(1 – t) > 0. Suy ra f(t) > 0.

Với t > 1 thì f(t) = t⁵(t³ – 1) + t(t – 1) + 1 > 0

Vậy f(t) > 0 ∀t ≥ 0. Suy ra: x⁴ – √x⁵ + x – √x + 1 > 0, ∀x ≥ 0.

Bài 6 trang 79 SGK Đại số lớp 10

Trong mặt phẳng tọa độ Oxy, trên các tia Ox, Oy lần lượt lấy các điểm A và B thay đổi sao cho đường thẳng AB luôn tiếp xúc với đường tròn tâm O bán kính 1. Xác định tọa độ của A và B để đoạn AB có độ dài nhỏ nhất.

Đáp án và hướng dẫn giải bài 6:

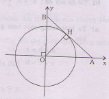
Ta có: 2S_OAB = AB.OH = AB (vì OH = 1).

Vậy diện tích ∆OAB nhỏ nhất khi AB có độ dài ngắn nhất.

Vì AB = AH + HB mà AH.HB = OH² = 1 nên AB có giá trị nhỏ nhất khi AH = HB tức ∆OAB vuông cân: OA = OB và

AB = 2AH = 2OH = 2.

AB² = 4 = 2OA2 = 2OH = OA = OB = √2.

Khi đó tọa độ của A, B là A(√2; 0) và B(0; √2).

------------------------------------------

Trên đây VnDoc đã giới thiệu tới bạn đọc tài liệu Giải bài tập trang 79 SGK Đại số 10: Bất đẳng thức. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu thêm tới các bạn học sinh tài liệu Toán lớp 10, Ngữ Văn 10, Tiếng Anh lớp 10,... mà VnDoc tổng hợp và đăng tải. Chúc các bạn ôn tập thật tốt!

Chia sẻ, đánh giá bài viết

5

4.008

Bài trước

Bài sau