Giải Toán lớp 10 Bài 4: Bất phương trình bậc nhất hai ẩn

Giải bài tập Toán 10

Giải Toán 10 Bài 4: Bất phương trình bậc nhất hai ẩn

VnDoc.com xin giới thiệu tới các em học sinh tài liệu Giải bài tập Toán 10: Bất phương trình bậc nhất hai ẩn, với cách giải bài tập rất chi tiết sẽ giúp các em học sinh học tập hiệu quả môn Toán lớp 10. Mời các bạn và thầy cô tham khảo.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 10, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 10 sau: Nhóm Tài liệu học tập lớp 10. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Giải bài tập trang 99 SGK Đại số 10: Bất phương trình bậc nhất hai ẩn

Bài 1 (trang 99 SGK Đại số 10): Biểu diễn hình học tập nghiệm của các bất phương trình bậc nhất hai ẩn sau:

$\begin{align} & a)-x+2+2\left( y-2 \right)<2\left( 1-x \right) \\ & b)3\left( x-1 \right)+4\left( y-2 \right)<5x-3 \\ \end{align}$ $\begin{align} & a)-x+2+2\left( y-2 \right)<2\left( 1-x \right) \\ & b)3\left( x-1 \right)+4\left( y-2 \right)<5x-3 \\ \end{align}$

Lời giải

a. Ta có: $-x+2+2\left( y-2 \right)<2\left( 1-x \right)$ $-x+2+2\left( y-2 \right)<2\left( 1-x \right)$

$\Leftrightarrow y<\frac{-x}{2}+2\text{ }\left( 1 \right)$ $\Leftrightarrow y<\frac{-x}{2}+2\text{ }\left( 1 \right)$

Biểu diễn tập nghiệm trên mặt phẳng tọa độ:

- Vẽ đường thẳng $y=\frac{-x}{2}+2$ $y=\frac{-x}{2}+2$

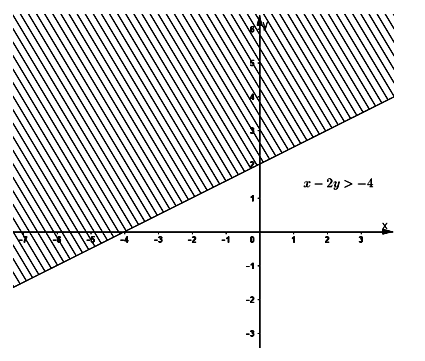
- Thay tọa độ O(0; 0) vào bất phương trình (1) ta thấy

$0<\frac{-1}{2}.0+2$ $0<\frac{-1}{2}.0+2$ (đúng)

Vậy (0; 0) là một nghiệm của bất phương trình.

Vậy tập nghiệm của bất phương trình là tập hợp các điểm trong miền không bị gạch sọc không kể bờ (với bờ là đường thẳng _{$y=\frac{-x}{2}+2$})

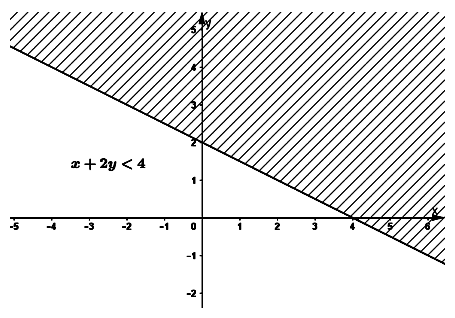
Giải Toán lớp 10 Bài 4: Bất phương trình bậc nhất hai ẩn

b. Ta có:

$\begin{align} & 3\left( x-1 \right)+4\left( y-2 \right)<5x-3 \\ & \Leftrightarrow y<\frac{1}{2}x+2 \\ \end{align}$ $\begin{align} & 3\left( x-1 \right)+4\left( y-2 \right)<5x-3 \\ & \Leftrightarrow y<\frac{1}{2}x+2 \\ \end{align}$

Biểu diễn tập nghiệm trên mặt phẳng tọa độ:

- Vẽ đường thẳng _{$y=\frac{1}{2}x+2$}

- Thay tọa độ O(0; 0) vào bất phương trình (1) ta thấy

$0<\frac{1}{2}.0+2$ $0<\frac{1}{2}.0+2$ đúng

Chứng tỏ (0; 0) là một nghiệm của bất phương trình.

Vậy nghiệm của bất phương trình là tập hợp các điểm trong miền không bị gạch sọc không kể bờ (với bờ là đường thẳng $y=\frac{1}{2}x+2$ $y=\frac{1}{2}x+2$)

Giải Toán lớp 10 Bài 4: Bất phương trình bậc nhất hai ẩn

Bài 2 (trang 99 SGK Đại số 10): Biểu diễn hình học tập nghiệm của các hệ bất phương trình bậc nhất hai ẩn sau:

$a.\left\{ \begin{matrix} x-2y<0 \\ x+3y>-2 \\ y-x<3 \\ \end{matrix} \right.$ $a.\left\{ \begin{matrix} x-2y<0 \\ x+3y>-2 \\ y-x<3 \\ \end{matrix} \right.$

$b.\left\{ \begin{matrix} \frac{x}{3}+\frac{y}{2}-1<0 \\ x+\frac{1}{2}-\frac{3y}{2}\le 2 \\ x\ge 0 \\ \end{matrix} \right.$ $b.\left\{ \begin{matrix} \frac{x}{3}+\frac{y}{2}-1<0 \\ x+\frac{1}{2}-\frac{3y}{2}\le 2 \\ x\ge 0 \\ \end{matrix} \right.$

Lời giải

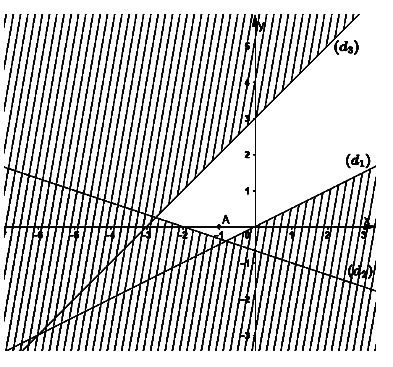
a. Miền nghiệm của hệ bất phương trình _{$\left\{ \begin{matrix} x-2y<0 \\ x+3y>-2 \\ y-x<3 \\ \end{matrix} \right.$} là phần mặt phẳng không bị gạch chéo được giời hạn bởi ba đường thẳng $y-x=3;x-2y=0;x+3y=-2$(không kể các bờ)

Giải Toán lớp 10 Bài 4: Bất phương trình bậc nhất hai ẩn

b. Ta có:

$\begin{align} & \left\{ \begin{matrix} \dfrac{x}{3}+\dfrac{y}{2}-1<0 \\ x+\dfrac{1}{2}-\dfrac{3y}{2}\le 2 \\ x\ge 0 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} \dfrac{2x+3y-6}{6}<0 \\ \dfrac{2x+1-3y-4}{2}\le 0 \\ x\ge 0 \\ \end{matrix} \right. \\ & \Leftrightarrow \left\{ \begin{matrix} 2x+3y-6<0 \\ 2x-3y-3\le 0 \\ x\ge 0 \\ \end{matrix} \right.\leftrightarrow \left\{ \begin{matrix} 2x+3y<6 \\ 2x-3y\le 3 \\ x\ge 0 \\ \end{matrix} \right. \\ \end{align}$ $\begin{align} & \left\{ \begin{matrix} \dfrac{x}{3}+\dfrac{y}{2}-1<0 \\ x+\dfrac{1}{2}-\dfrac{3y}{2}\le 2 \\ x\ge 0 \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} \dfrac{2x+3y-6}{6}<0 \\ \dfrac{2x+1-3y-4}{2}\le 0 \\ x\ge 0 \\ \end{matrix} \right. \\ & \Leftrightarrow \left\{ \begin{matrix} 2x+3y-6<0 \\ 2x-3y-3\le 0 \\ x\ge 0 \\ \end{matrix} \right.\leftrightarrow \left\{ \begin{matrix} 2x+3y<6 \\ 2x-3y\le 3 \\ x\ge 0 \\ \end{matrix} \right. \\ \end{align}$

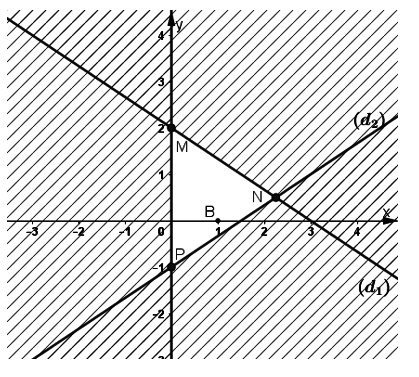
Ta vẽ các đường thẳng 2x + 3y = 6 (d1); 2x – 3y = 3 (d2); x = 0

Ta được kết quả như hình vẽ, miền không bị gạch chéo là miền nghiệm của bất phương trình đã cho

Giải Toán lớp 10 Bài 4: Bất phương trình bậc nhất hai ẩn

Bài 3 (trang 99 SGK Đại số 10). Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I, II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các loại máy thuộc các nhòm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:

Giải Toán lớp 10 Bài 4: Bất phương trình bậc nhất hai ẩn