Giải Toán 10 Bài 6: Hệ thức lượng trong tam giác KNTT

Giải Toán 10 sách Kết nối tri thức

Giải Toán 10 Bài 6 KNTT

Bài 3.5 trang 42 SGK Toán 10 KNTT
Bài 3.6 trang 42 SGK Toán 10 KNTT
Bài 3.7 trang 42 SGK Toán 10 KNTT
Bài 3.8 trang 42 SGK Toán 10 KNTT
Bài 3.9 trang 42 SGK Toán 10 KNTT
Bài 3.10 trang 43 SGK Toán 10 KNTT
Bài 3.11 trang 43 SGK Toán 10 KNTT

VnDoc.com xin gửi tới bạn đọc bài viết Giải Toán 10 Bài 6: Hệ thức lượng trong tam giác KNTT. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

Bài 3.5 trang 42 SGK Toán 10 KNTT

Cho tam giác ABC có a = 6, b = 5, c = 8. Tính cosA, S, r.

Lời giải

Hình vẽ minh họa

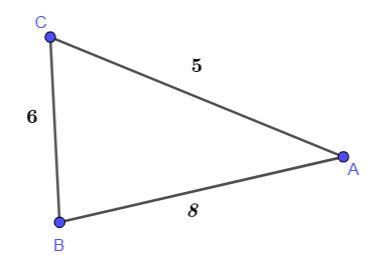
Giải Toán 10 Bài 6 KNTT

Xét tam giác ABC có:

$\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{5^2+8^2-6^2}{2.5.8}=0,6625$ $\cos A=\frac{b^2+c^2-a^2}{2bc}=\frac{5^2+8^2-6^2}{2.5.8}=0,6625$

$\Rightarrow\widehat A=48,51^0$ $\Rightarrow\widehat A=48,51^0$

=> sinA = 0,749

Diện tích tam giác ABC là:

$S_{ABC}=\frac12b.c.\sin A=\frac12.5.8.0,749=14,98$ $S_{ABC}=\frac12b.c.\sin A=\frac12.5.8.0,749=14,98$

Nửa chu vi của tam giác ABC là: $p=\frac{a+b+c}2=\frac{19}2$ $p=\frac{a+b+c}2=\frac{19}2$

Ta có: S = pr

$\Rightarrow r=\frac SP=\frac{14,98}{\displaystyle\frac{19}2}\approx1,58$ $\Rightarrow r=\frac SP=\frac{14,98}{\displaystyle\frac{19}2}\approx1,58$

Vậy cosA = 0,6625, S = 14,98 đvdt, r = 1,58.

Bài 3.6 trang 42 SGK Toán 10 KNTT

Cho tam giác ABC có $a=10;\widehat A=45^0;\widehat B=70^0$ $a=10;\widehat A=45^0;\widehat B=70^0$. Tính R, b, c.

Lời giải

Hình vẽ minh họa

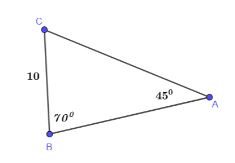
Giải Toán 10 Bài 6 KNTT

Xét tam giác ABC có:

$\widehat C=180^0-\widehat A-\widehat B=180^0-45^0-70^0=65^0$ $\widehat C=180^0-\widehat A-\widehat B=180^0-45^0-70^0=65^0$

Áp dụng định lý sin trong tam giác ta có:

$\frac a{\sin A}=\frac b{\sin B}=\frac c{\sin C}$ $\frac a{\sin A}=\frac b{\sin B}=\frac c{\sin C}$

=> $b=\frac{a.\sin B}{\sin A}=\frac{10.\sin70^0}{\sin45^0}\approx13,29$ $b=\frac{a.\sin B}{\sin A}=\frac{10.\sin70^0}{\sin45^0}\approx13,29$

Ta có: $\frac a{\sin A}=2R\Rightarrow R=\frac a{2.\sin A}=\frac{10}{2.\sin45^0}=5\sqrt2$ $\frac a{\sin A}=2R\Rightarrow R=\frac a{2.\sin A}=\frac{10}{2.\sin45^0}=5\sqrt2$

$\frac a{\sin A}=\frac c{\sin C}$ $\frac a{\sin A}=\frac c{\sin C}$

=> $c=\frac{a.\sin C}{\sin A}=\frac{10.\sin65^0}{\sin45^0}\approx12,82$ $c=\frac{a.\sin C}{\sin A}=\frac{10.\sin65^0}{\sin45^0}\approx12,82$

Vậy $R=5\sqrt2;b=13,29;c=12,82$ $R=5\sqrt2;b=13,29;c=12,82$

Bài 3.7 trang 42 SGK Toán 10 KNTT

Giải tam giác ABC và tính diện tích của tam giác đó, biết $\widehat A\;=\;15^o;\;\widehat B\;=\;130^o;\;c\;=\;6$ $\widehat A\;=\;15^o;\;\widehat B\;=\;130^o;\;c\;=\;6$

Lời giải

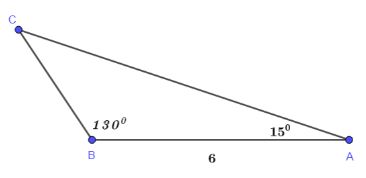
Giải Toán 10 Bài 6

Xét tam giác ABC có:

$\widehat C=180^0-\left(\widehat A+\widehat B\right)=180^0-\left(15^0+130^0\right)=35^0$ $\widehat C=180^0-\left(\widehat A+\widehat B\right)=180^0-\left(15^0+130^0\right)=35^0$

Áp dụng định lý sin trong tam giác ta có:

$\frac a{\sin A}=\frac b{\sin B}=\frac c{\sin C}$ $\frac a{\sin A}=\frac b{\sin B}=\frac c{\sin C}$

=> $\frac a{\sin15^0}=\frac b{\sin130^0}=\frac6{\sin35^0}$ $\frac a{\sin15^0}=\frac b{\sin130^0}=\frac6{\sin35^0}$

=> $\frac a{\sin15^0}=\frac6{\sin35^0}\Rightarrow a=\frac{6.\sin15^0}{\sin35^0}\approx2,71$ $\frac a{\sin15^0}=\frac6{\sin35^0}\Rightarrow a=\frac{6.\sin15^0}{\sin35^0}\approx2,71$

=> $\frac b{\sin130^0}=\frac6{\sin35^0}\Rightarrow b=\frac{6.\sin130^0}{\sin35^0}\approx8,01$ $\frac b{\sin130^0}=\frac6{\sin35^0}\Rightarrow b=\frac{6.\sin130^0}{\sin35^0}\approx8,01$

Diện tích tam giác ABC là:

$S=\frac12a\;.\;\;b.\;\sin\widehat C=\frac12\;.\;2,71\;\;.8,01\;.\;\sin35^0\approx\;9,2$ $S=\frac12a\;.\;\;b.\;\sin\widehat C=\frac12\;.\;2,71\;\;.8,01\;.\;\sin35^0\approx\;9,2$

Bài 3.8 trang 42 SGK Toán 10 KNTT

Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S70⁰E với vận tốc 70km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam theo vận tốc 8km/h. Sau 2 giờ kể từ khi bị hỏng, tàu neo đậu được vào một hòn đảo.

a) Tính khoảng cách từ cảng A tới nơi tàu neo đậu.

b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.

Lời giải

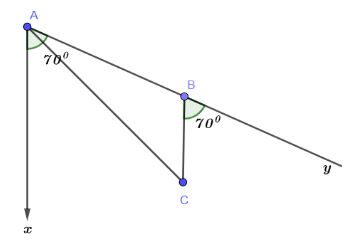
Giải Toán 10 Bài 6

a) Tàu cá xuất phát từ A đi theo hướng S70⁰E với vận tốc 70km/h trong 90 phút = 1,5 giờ thì tàu cá đi được đến B (vị trí tàu bị hỏng)

=> Quãng đường AB là: 70.1,5 = 105 (km)

Từ vị trí B tàu cá thả trôi với vận tốc 8km/h theo hướng nam sau 2h thì neo đậu vào đảo C

=> Quãng đường BC là: 8.2 = 16km

Khoảng cách từ cảng A đến nơi tàu neo đậu chính là đoạn AC.

Do tàu đi theo hướng S70⁰E nên phương AB hợp với phương nam Ax một góc 70⁰

=> $\widehat{xAB}=70^0$ $\widehat{xAB}=70^0$

Mà phương BC song song với phương nam Ax

=> $\widehat {CBx} = \widehat {xAB} = {70^0}$ $\widehat {CBx} = \widehat {xAB} = {70^0}$ (hai góc đồng vị)

=> $\widehat {ABC} = {110^0}$ $\widehat {ABC} = {110^0}$

Xét tam giác ABC ta có:

AC² = AB² + AC² – 2AB.AC.cosB

= 105² + 16² – 2.105.16.cos110⁰

= 12 430,19

=> AC = 111,49 km

Vậy khoảng cách từ cảng A đến nơi tàu neo đậu là 111,49 km.

b) Xét tam giác ABC, có:

$\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = \frac{{{{105}^2} + 111,{{49}^2} - {{16}^2}}}{{2.105.111,49}} \approx 0,99$ $\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = \frac{{{{105}^2} + 111,{{49}^2} - {{16}^2}}}{{2.105.111,49}} \approx 0,99$

$\Rightarrow \widehat {BAC} \approx 7,{75^0}$ $\Rightarrow \widehat {BAC} \approx 7,{75^0}$

$\Rightarrow \widehat {xAC} = {70^0} - \widehat {BAC} = {70^0} - 7,{75^0} = 62,{25^0}$ $\Rightarrow \widehat {xAC} = {70^0} - \widehat {BAC} = {70^0} - 7,{75^0} = 62,{25^0}$

Vậy hướng từ cảng A đến đảo nơi tàu neo đậu là S62,25⁰E.

Bài 3.9 trang 42 SGK Toán 10 KNTT

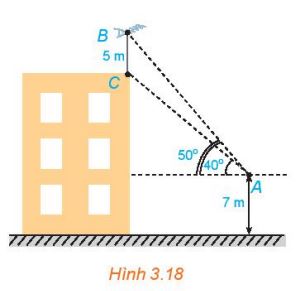
Trên nóc một tòa nhà có một cột ăng – ten cao 5m, Từ một vị trí quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng – ten, với các góc tương ứng là 50⁰ và 40⁰ so với phương nằm ngang (H.3.18).

a) Tính các góc của tam giác ABC.

b) Tính chiều cao của tòa nhà.

Giải Toán 10 Bài 6

Lời giải

Ký hiệu hình vẽ

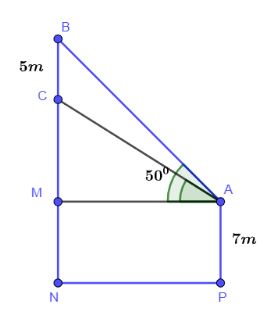
Giải Toán 10 Bài 6

Ta có: $\widehat {BAC} = {50^0} - {40^0} = {10^0}$ $\widehat {BAC} = {50^0} - {40^0} = {10^0}$

Xét tam giác Abm vuông tại M ta có:

$\widehat {CBA} + \widehat {BAM} = {90^0}$ $\widehat {CBA} + \widehat {BAM} = {90^0}$

=> $\widehat {CBA} = {90^0} - \widehat {BAM} = {90^0} - {50^0} = {40^0}$ $\widehat {CBA} = {90^0} - \widehat {BAM} = {90^0} - {50^0} = {40^0}$

Xét tam giác ABC ta có:

=> $\widehat {ACB} = {180^0} - \widehat {BAC} - \widehat {CBA} = {180^0} - {10^0} - {40^0} = {130^0}$ $\widehat {ACB} = {180^0} - \widehat {BAC} - \widehat {CBA} = {180^0} - {10^0} - {40^0} = {130^0}$

b) Xét tam giác ABC ta có:

$\frac{{AB}}{{\sin \widehat {BCA}}} = \frac{{BC}}{{\sin \widehat {BAC}}}$ $\frac{{AB}}{{\sin \widehat {BCA}}} = \frac{{BC}}{{\sin \widehat {BAC}}}$

$\Rightarrow \frac{{AB}}{{\sin {{130}^0}}} = \frac{5}{{\sin {{10}^0}}} \Rightarrow AB \approx 22,06\left( {ma} \right)$ $\Rightarrow \frac{{AB}}{{\sin {{130}^0}}} = \frac{5}{{\sin {{10}^0}}} \Rightarrow AB \approx 22,06\left( {ma} \right)$

Xét tam giác ABM có:

$BM = AB.\sin \widehat {BAC} = 22,06.\sin {50^0} \approx 16,9\left( m \right)$ $BM = AB.\sin \widehat {BAC} = 22,06.\sin {50^0} \approx 16,9\left( m \right)$

=> Chiều cao của tòa nhà là: 16,9 + 7 = 23,9 (m)

Vậy chiều cao của tòa nhà là 23,9 m.

Bài 3.10 trang 43 SGK Toán 10 KNTT

Từ bãi biển Vũng Chùa, Quảng Bình ta có thể ngắm được Đảo yến. Hãy đề xuất cách xác định bề rộng của hòn đảo (theo chiều ta ngắm được).

Giải Toán 10 Bài 6

Lời giải

Ta có hình vẽ minh họa:

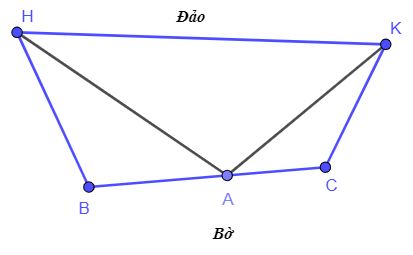
Giải Toán 10 Bài 6

Các bước xác định bề rộng của hòn đảo như sau:

Bước 1: Trên bờ, đặt một cọc ở vị trí A, một cọc ở vị trí B, một cọc ở vị trí C (như hình vẽ). Đo khoảng cách AB, AC

Bước 2: Đứng tại A ngắm điểm B và điểm H để đo góc tạo bởi hai hướng ngắm đó là góc BAH. Đứng tại B ngắm điểm H và điểm A để đo góc tạo bởi hai hướng ngắm đó là góc HBA.

Bước 3: Dựa vào định lí sin trong tam giác ABH ta tính được cạnh AH.

Bước 4: Đứng tại A ngắm điểm C và điểm K để đo góc tạo bởi hai hướng ngắm đó là góc KAC. Đứng tại C ngắm điểm K và điểm A để đo góc tạo bởi hai hướng ngắm đó là góc KCA

Bước 5: Dựa vào định lí sin trong tam giác AKC tính được AK.

Bước 6: Xét tam giác AKH, sử dụng định lí cos để tính cạnh KH.

Vậy độ dài KH chính là chiều rộng của đảo.

Bài 3.11 trang 43 SGK Toán 10 KNTT

Để tránh núi, đường giao thông hiện tại phải đi vòng như mô hình trong hình 3.19. Để rút ngắn khoảng cách và tránh sát lở núi, nối thẳng từ A đến D. Hỏi độ dài đường mới sẽ giảm bao nhiêu ki lô mét so với đường cũ?

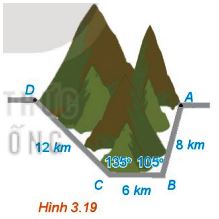
Giải Toán 10 Bài 6 KNTT

Lời giải

Ta có hình vẽ như sau:

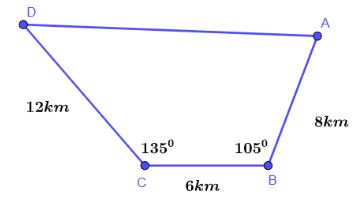
Giải Toán 10 Bài 6 KNTT

Xét ta giác ABC ta có:

AC² = AB² + BC² – 2AB.BC.cosB

= 8² + 6² – 2.8.6.cos105⁰

≈ 124,85

=> AC ≈ 11,17 km

=> $\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{AC}}{{\sin \widehat {ABC}}}$ $\frac{{AB}}{{\sin \widehat {ACB}}} = \frac{{AC}}{{\sin \widehat {ABC}}}$

$\Rightarrow \sin \widehat {ACB} = \frac{{AB.\sin \widehat {ABC}}}{{AC}} \approx 0,69$ $\Rightarrow \sin \widehat {ACB} = \frac{{AB.\sin \widehat {ABC}}}{{AC}} \approx 0,69$

$\Rightarrow \widehat {ACB} \approx 43,{77^0}$ $\Rightarrow \widehat {ACB} \approx 43,{77^0}$

$\Rightarrow \widehat {ACD} = \widehat {BCD} - \widehat {ACB} = {135^0} - 43,{77^0} = 91,{23^0}$ $\Rightarrow \widehat {ACD} = \widehat {BCD} - \widehat {ACB} = {135^0} - 43,{77^0} = 91,{23^0}$

Xét tam giác ADC ta có:

AD² = AC² + DC² – 2AC.DC.cosACD

= 11,17² + 12² – 2.11,17.12.cos91,23⁰

≈ 274,52

=> AD ≈ 16,57 km

Độ dài đoạn đường cũ là: AB + BC + CD = 8 + 6 + 12 = 26 km

Độ dài đường cũ hơn độ dài đoạn đường mới: 26 – 16,57 = 9,43 km.

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 6: Hệ thức lượng trong tam giác KNTT. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán 10 KNTT. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 KNTT, Tiếng Anh lớp 10...