Giải Toán 10 Bài 7: Các khái niệm mở đầu KNTT

Giải Toán 10 sách Kết nối tri thức

Giải Toán 10 Bài 7 KNTT

Bài 4.1 trang 50 SGK Toán 10 KNTT
Bài 4.2 trang 50 SGK Toán 10 KNTT
Bài 4.3 trang 50 SGK Toán 10 KNTT
Bài 4.4 trang 50 SGK Toán 10 KNTT
Bài 4.5 trang 50 SGK Toán 10 KNTT

Giải Toán 10 Bài 7: Các khái niệm mở đầu KNTT được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi bài viết dưới đây.

Bài 4.1 trang 50 SGK Toán 10 KNTT

Cho ba vecto $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ đều khác $\overrightarrow 0$ $\overrightarrow 0$. Những khẳng định nào sau đây đúng?

a) $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ đều cùng hướng với $\overrightarrow 0$ $\overrightarrow 0$

b) Nếu $\overrightarrow b$ $\overrightarrow b$ không cùng hướng với $\overrightarrow a$ $\overrightarrow a$ thì $\overrightarrow b$ $\overrightarrow b$ ngược hướng với $\overrightarrow a$ $\overrightarrow a$

c) Nếu $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ đều cùng phương với $\overrightarrow c$ $\overrightarrow c$ thì $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ cùng phương.

d) Nếu $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$đều cùng hướng với thì $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ cùng hướng.

Lời giải

a) $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ đều cùng hướng với $\overrightarrow 0$ $\overrightarrow 0$

Mọi vecto đều cùng hướng với $\overrightarrow 0$ $\overrightarrow 0$ => Khẳng định đúng

b) Nếu $\overrightarrow b$ $\overrightarrow b$ không cùng hướng với $\overrightarrow a$ $\overrightarrow a$ thì $\overrightarrow b$ $\overrightarrow b$ ngược hướng với $\overrightarrow a$ $\overrightarrow a$hoặc $\overrightarrow b$ $\overrightarrow b$ không cùng phương với $\overrightarrow a$ $\overrightarrow a$

=> Khẳng định sai

c) Nếu $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ đều cùng phương với $\overrightarrow c$ $\overrightarrow c$ thì $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ có giá song song hoặc trùng với $\overrightarrow c$ $\overrightarrow c$

=> $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ có giá song song hoặc trùng nhau

=> $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ cùng phương

=> Khẳng định đúng.

d) Nếu $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$đều cùng hướng với thì $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ cùng hướng.

=> Khẳng định đúng.

Bài 4.2 trang 50 SGK Toán 10 KNTT

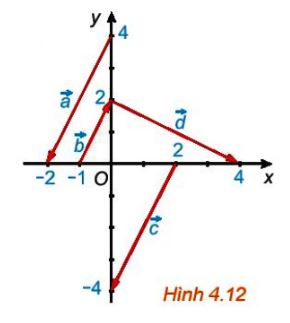
Trong hình 4.12 hãy chỉ ra các vecto cùng phương, các cặp vecto ngược hướng và các cặp vecto bằng nhau.

Giải Toán 10 Bài 7 KNTT

Lời giải

Quan sát hình vẽ ta thấy:

Các vecto $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ có giá song song với nhau và có cùng độ dài.

+ Các vecto cùng phương là: $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$

+ Các cặp vecto ngược hướng là: $\overrightarrow a ;\overrightarrow b$ $\overrightarrow a ;\overrightarrow b$ và $\overrightarrow c ;\overrightarrow b$ $\overrightarrow c ;\overrightarrow b$

+ Các cặp vecto cùng hướng và bằng nhau là: $\overrightarrow a ;\overrightarrow c$ $\overrightarrow a ;\overrightarrow c$

Bài 4.3 trang 50 SGK Toán 10 KNTT

Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi $\overrightarrow {BC} = \overrightarrow {AD}$ $\overrightarrow {BC} = \overrightarrow {AD}$

Lời giải

Hình vẽ minh họa

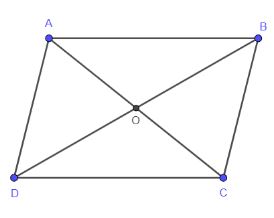
Giải Toán 10 Bài 7 KNTT

Nếu ABCD là hình bình hành => $\overrightarrow {AD} = \overrightarrow {BC}$ $\overrightarrow {AD} = \overrightarrow {BC}$

Chứng minh

Ta có: ABCD là hình bình hành

=> AD // BC

=> Hai vecto $\overrightarrow {AD} ;\overrightarrow {BC}$ $\overrightarrow {AD} ;\overrightarrow {BC}$ là hai vecto cùng phương

=> Hai vecto $\overrightarrow {AD} ;\overrightarrow {BC}$ $\overrightarrow {AD} ;\overrightarrow {BC}$ là hai vecto cùng hướng.

Mà AD = BC (tính chất hình bình hành)

=> $\overrightarrow {AD} = \overrightarrow {BC}$ $\overrightarrow {AD} = \overrightarrow {BC}$

Bài 4.4 trang 50 SGK Toán 10 KNTT

Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập hợp S gồm tất cả các vecto khác $\overrightarrow 0$ $\overrightarrow 0$ có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.

Lời giải

Hình vẽ minh họa

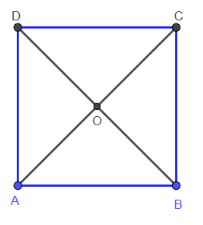
Giải Toán 10 Bài 7 KNTT

Các vecto khác $\overrightarrow 0$ $\overrightarrow 0$ có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O} là:

$\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} ;\overrightarrow {AO} ;$ $\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} ;\overrightarrow {AO} ;$

$\overrightarrow {BA} ;\overrightarrow {BC} ;\overrightarrow {BD} ;\overrightarrow {BO} ;$ $\overrightarrow {BA} ;\overrightarrow {BC} ;\overrightarrow {BD} ;\overrightarrow {BO} ;$

$\overrightarrow {CA} ;\overrightarrow {CB} ;\overrightarrow {CD} ;\overrightarrow {CO} ;$ $\overrightarrow {CA} ;\overrightarrow {CB} ;\overrightarrow {CD} ;\overrightarrow {CO} ;$

$\overrightarrow {DA} ;\overrightarrow {DB} ;\overrightarrow {DC} ;\overrightarrow {DO} ;$ $\overrightarrow {DA} ;\overrightarrow {DB} ;\overrightarrow {DC} ;\overrightarrow {DO} ;$

$\overrightarrow {OA} ;\overrightarrow {OB} ;\overrightarrow {OC} ;\overrightarrow {OD}$ $\overrightarrow {OA} ;\overrightarrow {OB} ;\overrightarrow {OC} ;\overrightarrow {OD}$

Khi đó tập hợp cần tìm là

$S = \left\{ {\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} ;\overrightarrow {AO} ;\overrightarrow {BA} ;\overrightarrow {BC} ;\overrightarrow {BD} ;\overrightarrow {BO} ;\overrightarrow {CA} ;\overrightarrow {CB} ;\overrightarrow {CD} ;\overrightarrow {CO} ;\overrightarrow {DA} ;\overrightarrow {DB} ;\overrightarrow {DC} ;\overrightarrow {DO} ;\overrightarrow {OA} ;\overrightarrow {OB} ;\overrightarrow {OC} ;\overrightarrow {OD} .} \right\}$ $S = \left\{ {\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} ;\overrightarrow {AO} ;\overrightarrow {BA} ;\overrightarrow {BC} ;\overrightarrow {BD} ;\overrightarrow {BO} ;\overrightarrow {CA} ;\overrightarrow {CB} ;\overrightarrow {CD} ;\overrightarrow {CO} ;\overrightarrow {DA} ;\overrightarrow {DB} ;\overrightarrow {DC} ;\overrightarrow {DO} ;\overrightarrow {OA} ;\overrightarrow {OB} ;\overrightarrow {OC} ;\overrightarrow {OD} .} \right\}$

Hai vecto bằng nhau trong tập hợp S là:

$\begin{matrix} \overrightarrow {AB} = \overrightarrow {DC} ;\overrightarrow {AD} = \overrightarrow {BC} ; \hfill \\ \overrightarrow {BA} = \overrightarrow {CD} ;\overrightarrow {DA} = \overrightarrow {CB} ; \hfill \\ \overrightarrow {OA} = \overrightarrow {CO} ;\overrightarrow {AO} = \overrightarrow {OC} ; \hfill \\ \overrightarrow {DO} = \overrightarrow {OB} ;\overrightarrow {OD} = \overrightarrow {BO} \hfill \\ \end{matrix}$ $\begin{matrix} \overrightarrow {AB} = \overrightarrow {DC} ;\overrightarrow {AD} = \overrightarrow {BC} ; \hfill \\ \overrightarrow {BA} = \overrightarrow {CD} ;\overrightarrow {DA} = \overrightarrow {CB} ; \hfill \\ \overrightarrow {OA} = \overrightarrow {CO} ;\overrightarrow {AO} = \overrightarrow {OC} ; \hfill \\ \overrightarrow {DO} = \overrightarrow {OB} ;\overrightarrow {OD} = \overrightarrow {BO} \hfill \\ \end{matrix}$

Khi đó tập S chia thành các nhóm là:

$\begin{matrix} \left\{ {\overrightarrow {AB} ;\overrightarrow {DC} } \right\} \hfill \\ \left\{ {\overrightarrow {AD} ;\overrightarrow {BC} } \right\} \hfill \\ \left\{ {\overrightarrow {BA} ;\overrightarrow {CD} } \right\} \hfill \\ \left\{ {\overrightarrow {DA} ;\overrightarrow {CB} } \right\} \hfill \\ \end{matrix}$ $\begin{matrix} \left\{ {\overrightarrow {AB} ;\overrightarrow {DC} } \right\} \hfill \\ \left\{ {\overrightarrow {AD} ;\overrightarrow {BC} } \right\} \hfill \\ \left\{ {\overrightarrow {BA} ;\overrightarrow {CD} } \right\} \hfill \\ \left\{ {\overrightarrow {DA} ;\overrightarrow {CB} } \right\} \hfill \\ \end{matrix}$

$\begin{matrix} \left\{ {\overrightarrow {OA} ;\overrightarrow {CO} } \right\} \hfill \\ \left\{ {\overrightarrow {AO} ;\overrightarrow {OC} } \right\} \hfill \\ \left\{ {\overrightarrow {DO} ;\overrightarrow {OB} } \right\} \hfill \\ \left\{ {\overrightarrow {OD} ;\overrightarrow {BO} } \right\} \hfill \\ \end{matrix}$ $\begin{matrix} \left\{ {\overrightarrow {OA} ;\overrightarrow {CO} } \right\} \hfill \\ \left\{ {\overrightarrow {AO} ;\overrightarrow {OC} } \right\} \hfill \\ \left\{ {\overrightarrow {DO} ;\overrightarrow {OB} } \right\} \hfill \\ \left\{ {\overrightarrow {OD} ;\overrightarrow {BO} } \right\} \hfill \\ \end{matrix}$

Bài 4.5 trang 50 SGK Toán 10 KNTT

Trên mặt phẳng tọa độ Oxy, hãy vẽ vecto $\overrightarrow {OA} ;\overrightarrow {MN}$ $\overrightarrow {OA} ;\overrightarrow {MN}$ với a(1; 2), m(0; -1), n(3; 5).

a) Chỉ ra mối quan hệ giữa hai vecto trên.

b) Một vật thể khởi hành từ M và chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn bởi vecto $\overrightarrow v = \overrightarrow {OA}$ $\overrightarrow v = \overrightarrow {OA}$. Hỏi vật thể đó có đi qua điểm N hay không? Nếu có thì sau bao lâu vật sẽ tới N?

Lời giải

Hình vẽ minh họa

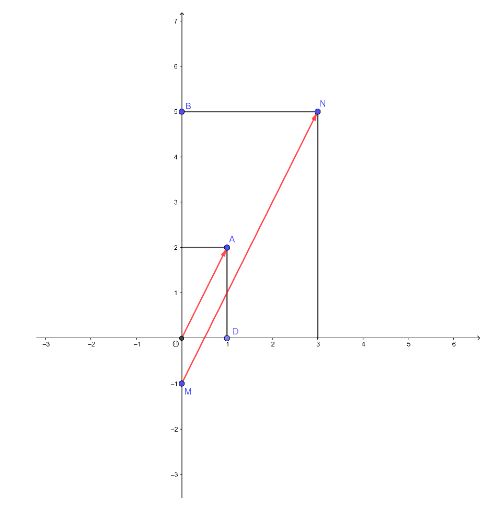
Giải Toán 10 Bài 7 KNTT

a) Quan sát hình vẽ ta thấy;

Hai vecto $\overrightarrow {OA} ;\overrightarrow {MN}$ $\overrightarrow {OA} ;\overrightarrow {MN}$ là hai vecto cùng hướng

b) Xét tam giác OAD vuông tạị D ta có:

OA² = OD² + AD²

=> OA² = 1² + 2² = 5

=> $OA = \sqrt 5$ $OA = \sqrt 5$

Xét tam giác MNB vuông tạo B ta có:

NM² = MB² + BN²

=> NM² = 6² + 3² = 45

=> $NM = 3\sqrt 5$ $NM = 3\sqrt 5$

Ta có: $\frac{{NM}}{{OA}} = \frac{{3\sqrt 5 }}{{\sqrt 5 }} = 3$ $\frac{{NM}}{{OA}} = \frac{{3\sqrt 5 }}{{\sqrt 5 }} = 3$

=> NM = 3OA

Do hai vecto $\overrightarrow {OA} ;\overrightarrow {MN}$ $\overrightarrow {OA} ;\overrightarrow {MN}$ là hai vecto cùng hướng nên vật thể chuyển động thẳng đều với vận tốc được biểu diễn $\overrightarrow v = \overrightarrow {OA}$ $\overrightarrow v = \overrightarrow {OA}$ nên vật thể đó đi qua điểm N và sau 3 giờ thì vật sẽ tới điểm N.

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 7: Các khái niệm mở đầu KNTT. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán 10 KNTT. Mời các bạn tham khảo thêm các môn Ngữ văn 10 KNTT, Tiếng Anh lớp 10...