Giải Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ KNTT

Giải Toán 10 sách Kết nối tri thức

Vectơ trong mặt phẳng tọa độ

Bài 4.16 trang 65 SGK Toán 10 KNTT
Bài 4.17 trang 65 SGK Toán 10 KNTT
Bài 4.18 trang 65 SGK Toán 10 KNTT
Bài 4.19 trang 65 SGK Toán 10 KNTT
Bài 4.20 trang 65 SGK Toán 10 KNTT

Giải Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ KNTT được VnDoc.com tổng hợp và gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây nhé.

Bài 4.16 trang 65 SGK Toán 10 KNTT

Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 3), N(4; 2)

a) Tính độ dài các đoạn thẳng OM, ON, MN.

b) Chứng minh rằng tam giác OMN vuông cân.

Gợi ý đáp án

a) Ta có: M(1; 3) và N (4; 2)

$\Rightarrow \overrightarrow {OM} (1;3),\;\,\overrightarrow {ON} (4;2),\;\overrightarrow {MN} = (4 - 1;2 - 3) = (3; - 1)$ $\Rightarrow \overrightarrow {OM} (1;3),\;\,\overrightarrow {ON} (4;2),\;\overrightarrow {MN} = (4 - 1;2 - 3) = (3; - 1)$

$\Rightarrow OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{1^2} + {3^2}} = \sqrt {10} ,ON = \left| {\overrightarrow {ON} } \right| = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 ,MN$ $\Rightarrow OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{1^2} + {3^2}} = \sqrt {10} ,ON = \left| {\overrightarrow {ON} } \right| = \sqrt {{4^2} + {2^2}} = 2\sqrt 5 ,MN$

$= \left| {\overrightarrow {MN} } \right| = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10}$ $= \left| {\overrightarrow {MN} } \right| = \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} = \sqrt {10}$

b) Dễ thấy: $OM = \sqrt {10} = MN \Rightarrow \Delta$ $OM = \sqrt {10} = MN \Rightarrow \Delta$ OMN cân tại M.

Lại có: $O{M^2} + M{N^2} = 10 + 10 = 20 = O{N^2}$ $O{M^2} + M{N^2} = 10 + 10 = 20 = O{N^2}$

Theo định lí Pythagore đảo, ta có $\Delta OMN$ $\Delta OMN$ vuông tại M.

Vậy $\Delta OMN$ $\Delta OMN$ vuông cân tại M.

Bài 4.17 trang 65 SGK Toán 10 KNTT

Trong mặt phẳng tọa độ Oxy, cho các vectơ $\overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j ,\overrightarrow b = \left( {4; - 1} \right)$ $\overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j ,\overrightarrow b = \left( {4; - 1} \right)$ và các điểm M (-3; 6), N(3; -3).

a) Tìm mối liên hệ giữa các vectơ $\overrightarrow {MN}$ $\overrightarrow {MN}$ và $2\;\overrightarrow a - \overrightarrow b .$ $2\;\overrightarrow a - \overrightarrow b .$

b) Các điểm O, M, N có thẳng hàng hay không?

c) Tìm điểm P(x; y) để OMNP là một hình bình hành.

Gợi ý đáp án

a) Ta có: $\overrightarrow b = \left( {4; - 1} \right) và \overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)$ $\overrightarrow b = \left( {4; - 1} \right) và \overrightarrow a = 3.\overrightarrow i - 2.\overrightarrow j \;\; \Rightarrow \;\overrightarrow a \;\left( {3; - 2} \right)$

$\Rightarrow 2\;\overrightarrow a - \overrightarrow b = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)$ $\Rightarrow 2\;\overrightarrow a - \overrightarrow b = \left( {2.3 - 4\;;\;2.\left( { - 2} \right) - \left( { - 1} \right)} \right) = \left( {2; - 3} \right)$

Lại có: M (-3; 6), N(3; -3)

$\Rightarrow \overrightarrow {MN} = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)$ $\Rightarrow \overrightarrow {MN} = \left( {3 - \left( { - 3} \right); - 3 - 6} \right) = \left( {6; - 9} \right)$

Dễ thấy: $\left( {6; - 9} \right) = 3.\left( {2; - 3} \right) \Rightarrow \overrightarrow {MN} = 3\left( {2\;\overrightarrow a - \overrightarrow b } \right)$ $\left( {6; - 9} \right) = 3.\left( {2; - 3} \right) \Rightarrow \overrightarrow {MN} = 3\left( {2\;\overrightarrow a - \overrightarrow b } \right)$

b) Ta có: $\overrightarrow {OM} = \left( { - 3;6} \right) ( do M(-3; 6)) và \overrightarrow {ON} = \left( {3; - 3} \right) (do N (3; -3)).$ $\overrightarrow {OM} = \left( { - 3;6} \right) ( do M(-3; 6)) và \overrightarrow {ON} = \left( {3; - 3} \right) (do N (3; -3)).$

Hai vectơ này không cùng phương (vì $\frac{-3}{3} \neq \frac{6}{-3}$ $\frac{-3}{3} \neq \frac{6}{-3}$ ).

Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.

Vậy chúng không thẳng hàng.

c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi $\overrightarrow {OM} = \overrightarrow {PN} .$ $\overrightarrow {OM} = \overrightarrow {PN} .$

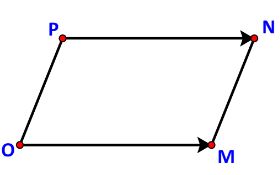
Giải Toán 10 Bài 10

Do $\overrightarrow {OM} = \left( { - 3;6} \right),\;\overrightarrow {PN} = \left( {3 - x; - 3 - y} \right)$ $\overrightarrow {OM} = \left( { - 3;6} \right),\;\overrightarrow {PN} = \left( {3 - x; - 3 - y} \right)$ nên

$\overrightarrow {OM} = \overrightarrow {PN} \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 = - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 9\end{array} \right.$ $\overrightarrow {OM} = \overrightarrow {PN} \Leftrightarrow \left\{ \begin{array}{l} - 3 = 3 - x\\6 = - 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 9\end{array} \right.$

Vậy điểm cần tìm là P (6; -9).

Bài 4.18 trang 65 SGK Toán 10 KNTT

Trong mặt phẳng tọa độ Oxy, cho các điểm A(1; 3), B(2; 4), C(-3; 2).

a) Hãy giải thích vì sao các điểm A, B, C không thẳng hàng.

b) Tìm tọa độ trung điểm M của đoạn thẳng AB.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm điểm D(x; y) để O(0; 0) là trọng tâm của tam giác ABD.

Gợi ý đáp án

a)

Ta có: $\overrightarrow {AB} = \left( {2 - 1;4 - 3} \right) = \left( {1;1} \right),\;\overrightarrow {AC} = \left( { - 3 - 1;2 - 3} \right) = \left( { - 4; - 1} \right)$ $\overrightarrow {AB} = \left( {2 - 1;4 - 3} \right) = \left( {1;1} \right),\;\overrightarrow {AC} = \left( { - 3 - 1;2 - 3} \right) = \left( { - 4; - 1} \right)$

Hai vectơ này không cùng phương (vì $\frac{1}{{ - 4}} \ne \frac{1}{{ - 1}}$ $\frac{1}{{ - 4}} \ne \frac{1}{{ - 1}}$)

Do đó các điểm A, B, C không cùng nằm trên một đường thẳng.

Vậy chúng không thẳng hàng.

b) Trung điểm M của đoạn thẳng AB có tọa độ là $\left( {\frac{{1 + 2}}{2};\frac{{3 + 4}}{2}} \right) = \left( {\frac{3}{2};\frac{7}{2}} \right)$ $\left( {\frac{{1 + 2}}{2};\frac{{3 + 4}}{2}} \right) = \left( {\frac{3}{2};\frac{7}{2}} \right)$

c) Trọng tâm G của tam giác ABC có tọa độ là $\left( {\frac{{1 + 2 + \left( { - 3} \right)}}{3};\frac{{3 + 4 + 2}}{3}} \right) = \left( {0;3} \right)$ $\left( {\frac{{1 + 2 + \left( { - 3} \right)}}{3};\frac{{3 + 4 + 2}}{3}} \right) = \left( {0;3} \right)$

d) Để O (0; 0) là trọng tâm của tam giác ABD thì $\left( {0;0} \right) = \left( {\frac{{{x_A} + {x_B} + {x_D}}}{3};\frac{{{y_A} + {y_B} + {y_D}}}{3}} \right)$ $\left( {0;0} \right) = \left( {\frac{{{x_A} + {x_B} + {x_D}}}{3};\frac{{{y_A} + {y_B} + {y_D}}}{3}} \right)$

$\Leftrightarrow \left( {0;0} \right) = \left( {\frac{{1 + 2 + x}}{3};\frac{{3 + 4 + y}}{3}} \right)$ $\Leftrightarrow \left( {0;0} \right) = \left( {\frac{{1 + 2 + x}}{3};\frac{{3 + 4 + y}}{3}} \right)$

$\begin{array}{l} \Leftrightarrow \left( {0;0} \right) = \left( {1 + 2 + x;3 + 4 + y} \right)\\ \Leftrightarrow \left( {0;0} \right) = \left( {x + 3;y + 7} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}0 = x + 3\\0 = y + 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 7\end{array} \right.\end{array}$ $\begin{array}{l} \Leftrightarrow \left( {0;0} \right) = \left( {1 + 2 + x;3 + 4 + y} \right)\\ \Leftrightarrow \left( {0;0} \right) = \left( {x + 3;y + 7} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}0 = x + 3\\0 = y + 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 7\end{array} \right.\end{array}$

Vậy tọa độ điểm D là (-3; -7).

Bài 4.19 trang 65 SGK Toán 10 KNTT

Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau:

Tàu khởi hành từ vị trí A(1; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vectơ $\overrightarrow v = \left( {3;4} \right)$ $\overrightarrow v = \left( {3;4} \right)$. Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.

Gợi ý đáp án

Gọi B(x; y) là vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.

Do tàu khởi hành từ A đi chuyển với vận tốc được biểu thị bởi vectơ $\overrightarrow v = \left( {3;4} \right)$ $\overrightarrow v = \left( {3;4} \right)$ nên cứ sau mỗi giờ, tàu đi chuyển được một quãng bằng $\left| {\overrightarrow v } \right|.$ $\left| {\overrightarrow v } \right|.$

Vậy sau 1,5 giờ tàu di chuyển tới B, ta được: $\overrightarrow {AB} = 1,5.\overrightarrow v$ $\overrightarrow {AB} = 1,5.\overrightarrow v$

$\begin{array}{l} \Leftrightarrow (x - 1;y - 2) = 1,5\;.\left( {3;4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 4,5\\y - 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5,5\\y = 8\end{array} \right.\end{array}$ $\begin{array}{l} \Leftrightarrow (x - 1;y - 2) = 1,5\;.\left( {3;4} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 4,5\\y - 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5,5\\y = 8\end{array} \right.\end{array}$

Vậy sau 1,5 tàu ở vị trí (trên mặt phẳng tọa độ) là B (5,5; 8).

Bài 4.20 trang 65 SGK Toán 10 KNTT

Trong hình 4.38, quân mã đang ở vị trí có tọa độ (1; 2). Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?

Giải Toán 10 Bài 10

Gợi ý đáp án

a) Quân mã đi theo đường chéo hình chữ nhật có chiều dài 3 ô, chiều rộng 2 ô.

Do đó, từ vị trí hiện tại, quân mã có thể đi đến các vị trí A, B, C, D, E, F như dưới đây:

A có tọa độ (3; 3)

B có tọa độ (3; 1)

C có tọa độ (2; 0)

D có tọa độ (0; 0)

E có tọa độ (0; 4)

F có tọa độ (2; 4)

Vậy quân mã có thể đi đến các vị trí A(3;3), B(3;1), C(2;0), D(0;0), E(0;4), F(2;4).

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ KNTT. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu học tập môn Toán 10 KNTT. Mời các bạn cùng tham khảo thêm tài liệu học tập môn Ngữ văn 10 KNTT...

Chia sẻ, đánh giá bài viết

1

727

Bài trước

Bài sau