Bài tập cuối chương 3 KNTT
Giải Toán 10 Bài tập cuối chương 3 KNTT
Bài tập cuối chương 3 KNTT được VnDoc.com sưu tầm và xin gửi tới bạn đọc. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây nhé.
Bài 3.12 trang 44 SGK Toán 10 KNTT
Cho tam giác ABC có 
\(\widehat B = {135^0}\). Khẳng định nào sau đây đúng?
a)
A. | B. | C. | D. |
b)
A. | B. | C. | D. |
c)
A. | B. |
C. | D. |
Lời giải
a) Đáp án D
b) Đáp án B
c) Đáp án D
Bài 3.13 trang 44 SGK Toán 10 KNTT
Cho tam giác ABC. Khẳng định nào sau đây là đúng?
a)
| A. \(S = \frac{{abc}}{{4r}}\) | B. \(r = \frac{{2S}}{{a + b + c}}\) |
| C. a2= b2+ c2 + 2bc . cosA | D. S = r . (a + b + c) |
b)
| A. sinA = sin(B + C) | B. cosA = cos(B + C) |
| C. cosA > 0 | D. sinA ≤ 0 |
Lời giải
a) \(S = pr = \frac{{abc}}{{4R}} = \frac{{\left( {a + b + c} \right).r}}{2}\)
=> Đáp án A và D là đáp án sai
Theo định lí cos, ta có: a2 = b2 + c2 - 2bc.cosA. Do đó C sai.
Ta có:
\(S = \frac{{\left( {a + b + c} \right).r}}{2} \Rightarrow r = \frac{{2S}}{{a + b + c}}\)
=> Đáp án B là đáp án đúng
b)
Ta có: \(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat A = {180^0} - \left( {\widehat B + \widehat C} \right)\)
\(\sin \widehat A = \sin \left[ {{{180}^0} - \left( {\widehat B + \widehat C} \right)} \right] = \sin \left( {\widehat B + \widehat C} \right)\) => Đáp án A đúng
\(\cos \widehat A = \cos \left[ {{{180}^0} - \left( {\widehat B + \widehat C} \right)} \right] = - \cos \left( {\widehat B + \widehat C} \right)\) => Đáp án B sai
Ta có: \(\cos A > 0\) khi \({0^0} < \widehat A < {90^0}\) => Đáp án C sai
Trong một tam giác ta có: \({0^0} \leqslant \widehat A \leqslant {180^0}\)
=> sin A ≥ 0
=> Đáp án D đúng
Chọn đáp án A
Bài 3.14 trang 44 SGK Toán 10 KNTT
Tính giá trị các biểu thức sau:
a) M = sin450.cos450+ sin300;
b) \(N = \sin {60^0}.\cos {30^0} + \frac{1}{2}\sin {45^0}.\cos {45^0}\)
c) P = 1 + tan2600;
d) \(Q = \frac{1}{{2{{\sin }^2}{{120}^0} - \cot {{120}^0}}}\)
Lời giải
a) M = sin450.cos450+ sin300
\(= \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} + \frac{1}{2} = \frac{1}{2} + \frac{1}{2} = 1\)
b) \(N = \sin {60^0}.\cos {30^0} + \frac{1}{2}\sin {45^0}.\cos {45^0}\)
\(\frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{1}{2}.\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} = \frac{3}{4} + \frac{1}{4} = 1\)
c) P = 1 + tan2600
= \(1 + {\left( {\sqrt 3 } \right)^2} = 1 + 3 = 4\)
d) \(Q = \frac{1}{{2{{\sin }^2}{{120}^0} - \cot {{120}^0}}}\)
\(= \frac{1}{{{{\sin }^2}60}} + \cot {60^0} = \frac{4}{3} + \frac{1}{{\sqrt 3 }} = \frac{{4 + \sqrt 3 }}{3}\)
Bài 3.15 trang 44 SGK Toán 10 KNTT
Cho tam giác ABC có \(\widehat B = {60^0};\widehat C = {45^0}\) , AC = 10. Tính a, R, S.r.
Lời giải
Hình vẽ minh họa:
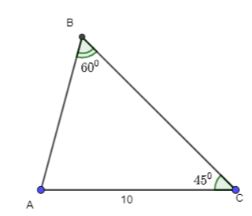
Xét tam giác ABC ta có:
\(\hat A = {180^0} - \hat B - \hat C = {180^0} - {60^0} - {45^0} = {75^0}\)
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
\(\Rightarrow \frac{{\text{a}}}{{\sin {\text{A}}}} = \frac{{\text{b}}}{{\sin {\text{B}}}} = \frac{{10}}{{\sin {{60}^0}}} = \frac{{10}}{{\dfrac{{\sqrt 3 }}{2}}} = \frac{{20}}{{\sqrt 3 }}\)
\(\Rightarrow {\text{a}} = \frac{{20}}{{\sqrt 3 }}\sin {\text{A}} = \frac{{20}}{{\sqrt 3 }}.\sin {75^0} = 11,15\)
\(\Rightarrow 2{\text{R}} = \frac{{\text{b}}}{{\sin {\text{B}}}} = \frac{{20}}{{\sqrt 3 }} \Leftrightarrow {\text{R}} = \frac{{10}}{{\sqrt 3 }}\)
Diện tích tam giác ABC là:
\(S = \frac{1}{2}.b.a.\sin C = \frac{1}{2}.10.11,15.\sin {45^0} \approx 39,42\)
\(\Rightarrow \frac{c}{{\sin C}} = \frac{b}{{\sin B}} = \frac{{20}}{{\sqrt 3 }} \Rightarrow c = \frac{{20}}{{\sqrt 3 }}.\sin C = \frac{{20}}{{\sqrt 3 }}.\sin {45^0} = \frac{{10\sqrt 6 }}{3}\)
Ta có:
\(S = p.r = \frac{{\left( {a + b + c} \right).r}}{2} \Rightarrow r = \frac{{2S}}{{a + b + c}} = 2,69\)
Bài 3.16 trang 44 SGK Toán 10 KNTT
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a) \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
b) \(M{A^2} + M{B^2} - A{B^2} = 2MA.MB.\cos \widehat {AMB}\) và \(M{A^2} + M{C^2} - A{C^2} = 2MA.MC.\cos \widehat {AMC}\)
c) \(M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\) (Công thức đường trung tuyến)
Lời giải
Hình vẽ minh họa
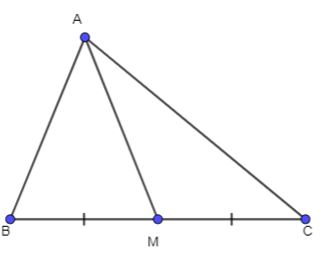
a) \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
Ta có: \(\widehat {AMB} + \widehat {AMC} = {180^0} \Rightarrow \widehat {AMC} = {180^0} - \widehat {AMB}\)
=> \(\cos \widehat {AMB} = - \cos \left( {{{180}^0} - \widehat {AMB}} \right) = - \cos \widehat {AMC}\)
=> \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\) => Điều phải chứng minh
b) \(M{A^2} + M{B^2} - A{B^2} = 2MA.MB.\cos \widehat {AMB}\) và \(M{A^2} + M{C^2} - A{C^2} = 2MA.MC.\cos \widehat {AMC}\)
Xét tam giác ABM ta có:
AB2 = MA2 + MB2 – 2MA.MB.cosAMB
=> MA2 + MB2 – AB2 = 2MA.MB.cosAMB (1)
Xét tam giác AMC, ta có:
AC2 = MA2 + MC2 – 2MA.MC.cosAMC
=> MA2 + MC2 – AC2 = 2MA.MC.cosAMC (2)
c) \(M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\) (Công thức đường trung tuyến)
Cộng vế với vế của (1) với (2), ta được:
MA2 + MB2 – AB2 + MA2 + MC2 – AC2 = 2MA.MB.cosAMB + 2MA.MC.cosAMC
\(\begin{matrix} 2M{A^2} + \frac{{B{C^2}}}{4} - A{B^2} + \frac{{B{C^2}}}{4} - A{C^2} \hfill \\ = 2MA \cdot \frac{{BC}}{2} \cdot \cos \widehat {AMB} + 2MA \cdot \frac{{BC}}{2} \cdot \cos \widehat {AMC}{\text{ (}}MB = MC = \frac{{BC}}{2}{\text{ ) }} \hfill \\ \end{matrix}\)
\(\begin{matrix} \Leftrightarrow 2{\text{M}}{{\text{A}}^2} + \frac{{{\text{B}}{{\text{C}}^2}}}{2} - {\text{A}}{{\text{B}}^2} - {\text{A}}{{\text{C}}^2} = 2{\text{MA}}{\text{.}}\frac{{{\text{BC}}}}{2}.(\cos \widehat {{\text{AMB}}} + \cos \widehat {{\text{AMC}}}) \hfill \\ \Leftrightarrow 2{\text{M}}{{\text{A}}^2} + \frac{{{\text{B}}{{\text{C}}^2}}}{2} - {\text{A}}{{\text{B}}^2} - {\text{A}}{{\text{C}}^2} = 0(\cos \widehat {{\text{AMB}}} + \cos \widehat {{\text{AMC}}} = 0) \Leftrightarrow 2{\text{M}}{{\text{A}}^2} = \frac{{2{\text{A}}{{\text{B}}^2} + 2{\text{A}}{{\text{C}}^2} - {\text{B}}{{\text{C}}^2}}}{2} \hfill \\ \end{matrix}\)
=> \(M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\)
Bài 3.17 trang 44 SGK Toán 10 KNTT
Cho tam giác ABC. Chứng minh rằng:
a) Nếu góc A nhọn thì b2 + c2 > a2;
b) Nếu góc A tù thì b2 + c2 < a2;
c) Nếu góc A vuông thì b2 + c2 = a2.
Lời giải
Xét tam giác ABC ta có:
Theo định lí cos, ta có: a2 = b2 + c2 – 2bc . cosA
a) Nếu góc A nhọn thì cosA > 0 ⇒ 2bc cosA > 0 ⇒ - 2bc cosA < 0
=> a2 = b2 + c2 – 2bc . cosA < b2 + c2
Vậy b2 + c2 > a2
b) Nếu góc A tù thì cosA > 0 ⇒ 2bccosA < 0 ⇒ - 2bc cosA > 0
=> a2 = b2 + c2 – 2bc . cosA > b2 + c2
Vậy b2 + c2 < a2.
c) Nếu góc A vuông thì cosA = 0 ⇒ 2bc cosA = 0
=> a2 = b2 + c2 – 2bc . cosA = b2 + c2
Vậy b2 + c2 = a2
Bài 3.18 trang 44 SGK Toán 10 KNTT
Trên biển, tàu B ở vị trí cách tàu A 53 km về hương N340E. Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu B.
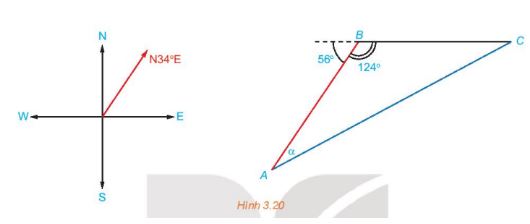
a) Hỏi tàu A cần phải chuyển động theo hướng nào?
b) Với hướng chuyển động đó thì sau bao lâu tàu A đuổi kịp tàu B?
Lời giải
a) Gọi thời gian tàu A đuổi kịp tàu B ở vị trí C là x (giờ) (x > 0)
Vì tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h đến C nên quãng đường BC là 30x (km)
Vì tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu B nên quãng đường AC là 50x (km)
Xét tam giác ABC ta có:
AC2 = BC2 + AB2 – 2AB . BC . cosB
=> 2500x2 = 900x2 + 532 – 2 . 53 . 30x . cos1240
=> 1600x2 – 1778x – 2809 = 0
\(\left[ {\begin{array}{*{20}{c}} {x \approx 1,99\left( {tm} \right)} \\ {x \approx - 0,88\left( {ktm} \right)} \end{array}} \right.\)
Do đó tàu A mất 1,99 giờ đuổi kịp tàu B.
=> BC = 30 . x = 30 . 1,99 = 59,7; AC = 50 . x = 50 . 1,99 = 99,5
Ta lại có:
\(\begin{matrix} \dfrac{{BC}}{{\sin A}} = \dfrac{{AC}}{{\sin B}} \Rightarrow \dfrac{{59,7}}{{\sin A}} = \dfrac{{99,5}}{{\sin {{124}^0}}} \hfill \\ \Rightarrow \sin A \approx 0,497 \Rightarrow \widehat B \approx 29,{83^0} \hfill \\ \end{matrix}\)
=> AC hợp với phương nam một góc 340 + 29,830 = 63,830
Vậy tàu A chuyển động theo hướng N63,830E
Bài 3.19 trang 44 SGK Toán 10 KNTT
Trên sân bóng chày dành cho nam, các vị trí gôn nhà (Home plate), gôn 1 (First base), gôn 2(Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4m. Vị trí đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2 và cách gôn nhà 18,44m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.
Lời giải
Hình vẽ minh họa:
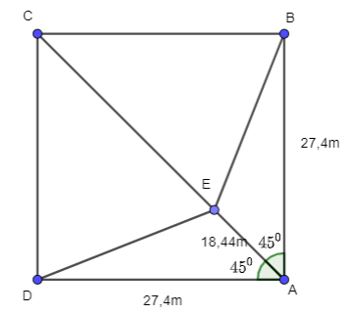
A là vị trí gôn nhà, B là vị trí gôn 1, C là vị trí gôn 2, D là vị trí gôn 3, E là vị trí ném bóng.
Xét tam giác ABE ta có:
BE2 = AB2 + AE2 – 2.AB.AE.cos
=> BE2 = 27,42 + 18,442 – 2.27,4.18,44.cos450
=> BE2 ≈ 376,25
=> BE ≈ 19,4 m.
Xét tam giác ABE và tam giác ADE ta có:
AB = AD (gt)
AE chung
\(\widehat {BAE} = \widehat {DAE} = {45^0}\)
=> ΔABE = ΔCDE (c – g – c)
=> BE = DE (hai cạnh tương ứng)
=> DE ≈ 19,4 m
Vậy khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3 là 19,4 m.
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Bài tập cuối chương 3 KNTT. Bài viết đã hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 KNTT. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 KNTT, Tiếng Anh lớp 10...
