Giải Toán 10 Bài 9: Tích của một vecto với một số KNTT

Giải Toán 10 sách Kết nối tri thức

Giải Toán 10 Bài 9 KNTT

Bài 4.11 trang 58 SGK Toán 10 KNTT
Bài 4.12 trang 58 SGK Toán 10 KNTT
Bài 4.13 trang 58 SGK Toán 10 KNTT
Bài 4.14 trang 58 SGK Toán 10 KNTT
Bài 4.15 trang 58 SGK Toán 10 KNTT

VnDoc.com xin gửi tới bạn đọc bài viết Giải Toán 10 Bài 9: Tích của một vecto với một số KNTT. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

Bài 4.11 trang 58 SGK Toán 10 KNTT

Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị $\overrightarrow {AM}$ $\overrightarrow {AM}$ theo hai vecto $\overrightarrow {AB}$ $\overrightarrow {AB}$ và $\overrightarrow {AD}$ $\overrightarrow {AD}$

Lời giải

Hình vẽ minh họa

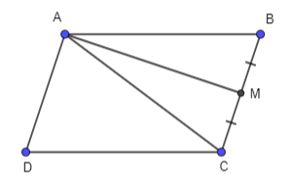
Giải Toán 10 Bài 9 KNTT

Gọi E là điểm đối xứng với A qua M. Khi đó ABEC là hình bình hành

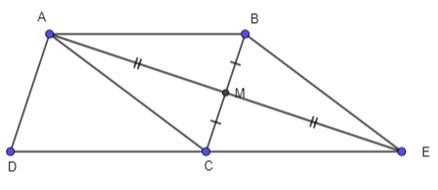
Giải Toán 10 Bài 9 KNTT

Ta có:

$\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AE}$ $\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AE}$(Quy tắc hình bình hành)

Mà $\overrightarrow {AE} = 2\overrightarrow {AM}$ $\overrightarrow {AE} = 2\overrightarrow {AM}$

=> $\overrightarrow {AM} = \frac{{\overrightarrow {AB} + \overrightarrow {AC} }}{2}$ $\overrightarrow {AM} = \frac{{\overrightarrow {AB} + \overrightarrow {AC} }}{2}$

Ta lại có: $\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD}$ $\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD}$ (Quy tắc hình bình hành)

=> $\overrightarrow {AM} = \frac{{\overrightarrow {AB} + \overrightarrow {AB} + \overrightarrow {AD} }}{2}$ $\overrightarrow {AM} = \frac{{\overrightarrow {AB} + \overrightarrow {AB} + \overrightarrow {AD} }}{2}$

=> $\frac{{2\overrightarrow {AB} + \overrightarrow {AD} }}{2} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD}$ $\frac{{2\overrightarrow {AB} + \overrightarrow {AD} }}{2} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD}$

Vậy $\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD}$ $\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD}$

Bài 4.12 trang 58 SGK Toán 10 KNTT

Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng: $\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD}$ $\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD}$

Lời giải

Hình vẽ minh họa

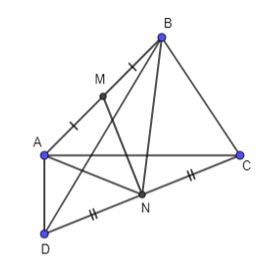
Giải Toán 10 Bài 9 KNTT

Ta có:

$\begin{matrix} \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {BC} + \overrightarrow {CD} \hfill \\ = \left( {\overrightarrow {AD} + \overrightarrow {DC} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) \hfill \\ = \overrightarrow {AD} + \overrightarrow {BC} \left( * \right) \hfill \\ \end{matrix}$ $\begin{matrix} \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {BC} + \overrightarrow {CD} \hfill \\ = \left( {\overrightarrow {AD} + \overrightarrow {DC} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {CD} } \right) \hfill \\ = \overrightarrow {AD} + \overrightarrow {BC} \left( * \right) \hfill \\ \end{matrix}$

Ta lại có:

$\begin{matrix} \overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {NC} - \overrightarrow {NB} + \overrightarrow {ND} - \overrightarrow {NA} \hfill \\ = \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) - \left( {\overrightarrow {NB} + \overrightarrow {NA} } \right) \hfill \\ = - \left( {\overrightarrow {NB} + \overrightarrow {NA} } \right) = - 2\overrightarrow {NM} = 2\overrightarrow {MN} \left( {**} \right) \hfill \\ \end{matrix}$ $\begin{matrix} \overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {NC} - \overrightarrow {NB} + \overrightarrow {ND} - \overrightarrow {NA} \hfill \\ = \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) - \left( {\overrightarrow {NB} + \overrightarrow {NA} } \right) \hfill \\ = - \left( {\overrightarrow {NB} + \overrightarrow {NA} } \right) = - 2\overrightarrow {NM} = 2\overrightarrow {MN} \left( {**} \right) \hfill \\ \end{matrix}$

Từ (*) và (**) suy ra: $\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD}$ $\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD}$

Bài 4.13 trang 58 SGK Toán 10 KNTT

Cho hai điểm phân biệt A và B.

a) Hãy xác định điểm K sao cho $\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0$ $\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0$

b) Chứng minh rằng với mọi điểm O, ta có: $\overrightarrow {OK} = \frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB}$ $\overrightarrow {OK} = \frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB}$

Lời giải

a) Gọi I là trung điểm của đoạn thẳng AB, ta có: $\overrightarrow {IB} + \overrightarrow {IB} = \overrightarrow 0$ $\overrightarrow {IB} + \overrightarrow {IB} = \overrightarrow 0$

Khi đó: $\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0$ $\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0$

=> $\overrightarrow {KI} + \overrightarrow {IA} + 2\overrightarrow {KI} + 2\overrightarrow {IB} = \overrightarrow 0$ $\overrightarrow {KI} + \overrightarrow {IA} + 2\overrightarrow {KI} + 2\overrightarrow {IB} = \overrightarrow 0$

=> $\left( {\overrightarrow {KI} + 2\overrightarrow {KI} } \right) + \overrightarrow {IB} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) = \overrightarrow 0$ $\left( {\overrightarrow {KI} + 2\overrightarrow {KI} } \right) + \overrightarrow {IB} + \left( {\overrightarrow {IA} + \overrightarrow {IB} } \right) = \overrightarrow 0$

=> $3\overrightarrow {KI} + \overrightarrow {IB} = \overrightarrow 0$ $3\overrightarrow {KI} + \overrightarrow {IB} = \overrightarrow 0$

=> $\overrightarrow {KI} = \frac{1}{3}\overrightarrow {BI}$ $\overrightarrow {KI} = \frac{1}{3}\overrightarrow {BI}$

Suy ra vecto $\overrightarrow {KI}$ $\overrightarrow {KI}$ cùng hướng với vecto $\overrightarrow {BI}$ $\overrightarrow {BI}$ và thỏa mãn $KI = \frac{1}{3}BI$ $KI = \frac{1}{3}BI$

Điểm K là điểm nằm giữa I và B và thỏa mãn $KI = \frac{1}{3}BI$ $KI = \frac{1}{3}BI$

Giải Toán 10 Bài 9 KNTT

b) Lấy điểm O bất kì ta có:

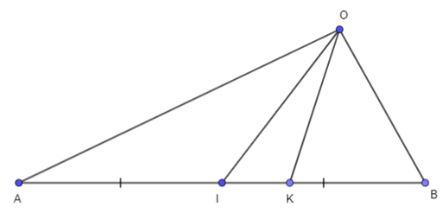
Giải Toán 10 Bài 9 KNTT

Ta có:

$\begin{matrix} VP = \dfrac{1}{3}\overrightarrow {OA} + \dfrac{2}{3}\overrightarrow {OB} \hfill \\ = \dfrac{1}{3}\left( {\overrightarrow {OK} + \overrightarrow {KA} } \right) + \dfrac{2}{3}\left( {\overrightarrow {OK} + \overrightarrow {KB} } \right) \hfill \\ = \dfrac{1}{3}\overrightarrow {OK} + \dfrac{1}{3}\overrightarrow {KA} + \dfrac{2}{3}\overrightarrow {OK} + \dfrac{2}{3}\overrightarrow {KB} \hfill \\ = \left( {\dfrac{1}{3}\overrightarrow {OK} + \dfrac{2}{3}\overrightarrow {OK} } \right) + \left( {\dfrac{1}{3}\overrightarrow {KA} + \dfrac{2}{3}\overrightarrow {KB} } \right) \hfill \\ \end{matrix}$ $\begin{matrix} VP = \dfrac{1}{3}\overrightarrow {OA} + \dfrac{2}{3}\overrightarrow {OB} \hfill \\ = \dfrac{1}{3}\left( {\overrightarrow {OK} + \overrightarrow {KA} } \right) + \dfrac{2}{3}\left( {\overrightarrow {OK} + \overrightarrow {KB} } \right) \hfill \\ = \dfrac{1}{3}\overrightarrow {OK} + \dfrac{1}{3}\overrightarrow {KA} + \dfrac{2}{3}\overrightarrow {OK} + \dfrac{2}{3}\overrightarrow {KB} \hfill \\ = \left( {\dfrac{1}{3}\overrightarrow {OK} + \dfrac{2}{3}\overrightarrow {OK} } \right) + \left( {\dfrac{1}{3}\overrightarrow {KA} + \dfrac{2}{3}\overrightarrow {KB} } \right) \hfill \\ \end{matrix}$

Do $\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0$ $\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0$

$= \overrightarrow {OK} + \frac{1}{3}.\left( {\overrightarrow {KA} + 2\overrightarrow {KB} } \right) = \overrightarrow {OK} = VT$ $= \overrightarrow {OK} + \frac{1}{3}.\left( {\overrightarrow {KA} + 2\overrightarrow {KB} } \right) = \overrightarrow {OK} = VT$

Bài 4.14 trang 58 SGK Toán 10 KNTT

Cho tam giác ABC.

a) Hãy xác định điểm M để $\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0$ $\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0$

b) Chứng minh rằng với mọi điểm O, ta có: $\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM}$ $\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM}$

Lời giải

a) Gọi G là trọng tâm của tam giác ABC ta có: $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0$ $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0$

Xét $\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0$ $\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0$

=> $\overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + 2\left( {\overrightarrow {MG} + \overrightarrow {GC} } \right) = \overrightarrow 0$ $\overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + 2\left( {\overrightarrow {MG} + \overrightarrow {GC} } \right) = \overrightarrow 0$

=> $4\overrightarrow {MG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + \overrightarrow {GC} = \overrightarrow 0$ $4\overrightarrow {MG} + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + \overrightarrow {GC} = \overrightarrow 0$

=> $4\overrightarrow {MG} + \overrightarrow {GC} = \overrightarrow 0$ $4\overrightarrow {MG} + \overrightarrow {GC} = \overrightarrow 0$

=> $\overrightarrow {MG} = \frac{1}{4}\overrightarrow {CG}$ $\overrightarrow {MG} = \frac{1}{4}\overrightarrow {CG}$

Suy ra điểm M nằm giữa C và G sao cho $MG = \frac{1}{4}.CG$ $MG = \frac{1}{4}.CG$

Hình vẽ minh họa

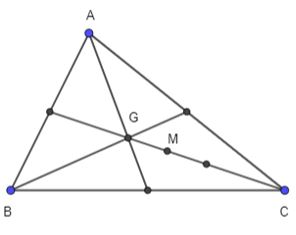
Giải Toán 10 Bài 9 KNTT

b) Xét vế trái ta có:

$\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC}$ $\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC}$

= $\overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {OM} + \overrightarrow {MB} + \overrightarrow {2OM} + \overrightarrow {2MC}$ $\overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {OM} + \overrightarrow {MB} + \overrightarrow {2OM} + \overrightarrow {2MC}$

= $4\overrightarrow {OM} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {2MC} } \right)$ $4\overrightarrow {OM} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {2MC} } \right)$

Ta có: $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {2MC} = \overrightarrow 0$ $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {2MC} = \overrightarrow 0$

= $4\overrightarrow {OM} = VP$ $4\overrightarrow {OM} = VP$

Bài 4.15 trang 58 SGK Toán 10 KNTT

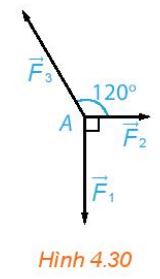
Chất điểm A chịu tác động của ba lực $\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}}$ $\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}}$ như hình 4.30 và ở trạng thái cân bằng (tức là $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0$ $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0$ ). Tính độ lớn của các lực $\overrightarrow {{F_2}} ;\overrightarrow {{F_3}}$ $\overrightarrow {{F_2}} ;\overrightarrow {{F_3}}$ và $\overrightarrow {{F_1}}$ $\overrightarrow {{F_1}}$ có độ lớn là 20N.

Giải Toán 10 Bài 9 KNTT

Lời giải

Hình vẽ minh họa:

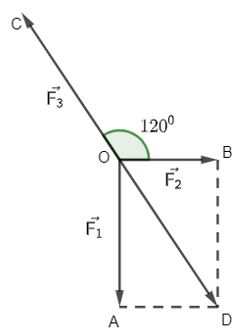
Giải Toán 10 Bài 9 KNTT

Ta có: $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0$ $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0$

=> $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = - \overrightarrow {{F_3}}$ $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = - \overrightarrow {{F_3}}$

Mà $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD}$ $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD}$ (OBDA là hình bình hành)

=> $\overrightarrow {OD} = - \overrightarrow {{F_3}}$ $\overrightarrow {OD} = - \overrightarrow {{F_3}}$

=> Hai vecto $\overrightarrow {OD} ;\overrightarrow {{F_3}}$ $\overrightarrow {OD} ;\overrightarrow {{F_3}}$ là hai vecto đối nhau

=> $\left| {\overrightarrow {OD} } \right| = \left| { - \overrightarrow {{F_3}} } \right|$ $\left| {\overrightarrow {OD} } \right| = \left| { - \overrightarrow {{F_3}} } \right|$ và $\widehat {BOD} = {60^0}$ $\widehat {BOD} = {60^0}$

Ta lại có: $\overrightarrow {BD} = \overrightarrow {{F_1}}$ $\overrightarrow {BD} = \overrightarrow {{F_1}}$

Xét tam giác OBD ta có:

$OB = \frac{{BD}}{{\tan {{60}^0}}} = \frac{{20}}{{\sqrt 3 }}\left( N \right)$ $OB = \frac{{BD}}{{\tan {{60}^0}}} = \frac{{20}}{{\sqrt 3 }}\left( N \right)$

=> $\left| {\overrightarrow {{F_2}} } \right| = \frac{{20}}{{\sqrt 3 }}\left( N \right)$ $\left| {\overrightarrow {{F_2}} } \right| = \frac{{20}}{{\sqrt 3 }}\left( N \right)$

$OD = \frac{{BD}}{{\sin {{60}^0}}} = \frac{{40\sqrt 3 }}{3}\left( N \right)$ $OD = \frac{{BD}}{{\sin {{60}^0}}} = \frac{{40\sqrt 3 }}{3}\left( N \right)$

=> $\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}\left( N \right)$ $\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}\left( N \right)$

Vậy độ lơn hai vecto $\overrightarrow {{F_2}} ;\overrightarrow {{F_3}}$ $\overrightarrow {{F_2}} ;\overrightarrow {{F_3}}$ lần lượt $\frac{{20}}{{\sqrt3 }}N;\frac{{40\sqrt 3 }}{3}N$ $\frac{{20}}{{\sqrt3 }}N;\frac{{40\sqrt 3 }}{3}N$

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 9: Tích của một vecto với một số KNTT. Bài viết đã hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 KNTT. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 KNTT, Tiếng Anh lớp 10...

Chia sẻ, đánh giá bài viết

1

806

Bài trước

Bài sau