Giải Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ KNTT

Giải Toán 10 sách Kết nối tri thức

Giải Toán 10 KNTT Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Bài 3.1 trang 37 SGK Toán 10 KNTT Tập 1
Bài 3.2 trang 37 SGK Toán 10 KNTT Tập 1
Bài 3.3 trang 37 SGK Toán 10 KNTT Tập 1
Bài 3.4 trang 37 SGK Toán 10 KNTT Tập 1

Giải Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ KNTT vừa được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 10. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

Bài 3.1 trang 37 SGK Toán 10 KNTT Tập 1

Không dùng bảng số hay máy tính cầm tay, tính giá trị các biểu thức sau:

a) (2sin30⁰ + cos135⁰ – 3tan150⁰).(cos180⁰ – cot60⁰);

b) sin²90⁰ + cos²120⁰ + cos²0⁰ – tan²60⁰ + cot²135⁰;

c) cos60⁰.sin30⁰ + cos²30⁰.

Chú ý: sin²α=(sinα)²,cos²α=(cosα)²,

tan²α=(tanα)₂,cot²α=(cotα)².

Lời giải

a) (2sin300 + cos1350 – 3tan1500).(cos1800 – cot600)

= (2sin300 – cos450 + 3tan300).(-1 – tan300)

$=(2\frac12-\frac{\sqrt2}2+3\frac{\sqrt3}3)(-1-\frac{\sqrt3}3)$ $=(2\frac12-\frac{\sqrt2}2+3\frac{\sqrt3}3)(-1-\frac{\sqrt3}3)$

$=\;(1-\frac{\sqrt2}2+\sqrt3)(\frac{-1-\sqrt3}{\sqrt3})$ $=\;(1-\frac{\sqrt2}2+\sqrt3)(\frac{-1-\sqrt3}{\sqrt3})$

≈ –3,194

b) sin²90⁰ + cos²120⁰ + cos²0⁰ – tan²60⁰ + cot²135⁰

= sin²90⁰ + cos²120⁰ + cos²0⁰ – tan²60⁰ + cot²45⁰

^{$=\;1+\;{(\frac12)}^2\;+1-{(\sqrt3)}^2+1$}

^{$=\;1+\frac14+1-3+1=\frac14$}

c) cos60⁰.sin30⁰ + cos²30⁰

$=\;\frac12.\frac12+\left(\frac{\sqrt3}2\right)^2$ $=\;\frac12.\frac12+\left(\frac{\sqrt3}2\right)^2$

$=\;\frac14+\frac34=\frac44=1$ $=\;\frac14+\frac34=\frac44=1$

Bài 3.2 trang 37 SGK Toán 10 KNTT Tập 1

Đơn giản các biểu thức sau:

a) sin100⁰ + sin80⁰ + cos16⁰ + cos 164⁰;

b) 2sin(180⁰ – α)cotα – cos(180⁰ – α).tanα.cos(180⁰ – α) với 0⁰ < α < 90⁰.

Lời giải

a) sin100⁰ + sin80⁰ + cos16⁰ + cos 164⁰

= sin100⁰ + sin100⁰ + cos 164⁰ + cos 164⁰

= 2sin100⁰ + 2cos 164⁰.

b) 2sin(180⁰ – α)cotα – cos(180⁰ – α).tanα.cos(180⁰ – α) với 0⁰ < α < 90⁰

=2sinαcotα−cosα.tanα.cotα

$=\;2\;\sin\;\alpha\;\frac{\cos\alpha}{\sin\alpha}-\cos\alpha.\frac{\sin\alpha}{\cos\alpha}.\frac{\cos\alpha}{\sin\alpha}$ $=\;2\;\sin\;\alpha\;\frac{\cos\alpha}{\sin\alpha}-\cos\alpha.\frac{\sin\alpha}{\cos\alpha}.\frac{\cos\alpha}{\sin\alpha}$

=2cosα−cosα=cosα

Bài 3.3 trang 37 SGK Toán 10 KNTT Tập 1

Chứng minh các hệ thức sau:

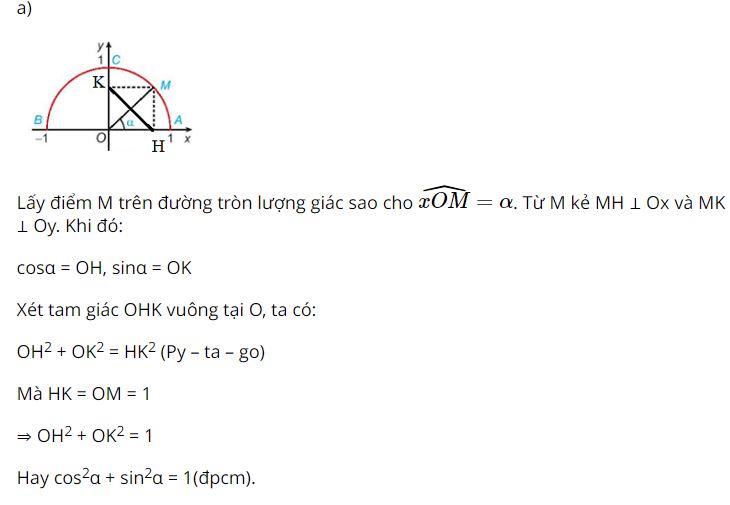
a) sin²α + cos²α = 1;

b) $1\;+\;\tan^2\alpha\;=\;\frac1{\cos^2\alpha}\;(\alpha\;\neq\;90^0)$ $1\;+\;\tan^2\alpha\;=\;\frac1{\cos^2\alpha}\;(\alpha\;\neq\;90^0)$

c) $1\;+\;cot^2\alpha\;=\;\frac1{\sin^2\alpha}(\;0^0<\;\alpha\;<\;180^0)\;.$ $1\;+\;cot^2\alpha\;=\;\frac1{\sin^2\alpha}(\;0^0<\;\alpha\;<\;180^0)\;.$

Lời giải

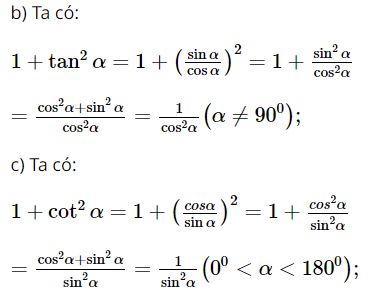
Giải Toán 10 Bài 5

Bài 3.4 trang 37 SGK Toán 10 KNTT Tập 1

Cho góc α ( 00 < α < 1800) thỏa mãn α = 3.

Tính giá trị của biểu thức: $P\;=\frac{2\;\sin\;\alpha\;-\;3\;cos\;\alpha}{3\;\sin\;\alpha\;+\;2\;cos\;\alpha}$ $P\;=\frac{2\;\sin\;\alpha\;-\;3\;cos\;\alpha}{3\;\sin\;\alpha\;+\;2\;cos\;\alpha}$

Lời giải

Chia cả tử và mẫu của biểu thức P cho cosα ≠ 0 với 0⁰ < α < 180⁰ ta được:

$P\;=\;\frac{2.{\displaystyle\frac{\sin\alpha}{cos\;\alpha}}-3}{3.{\displaystyle\frac{\sin\alpha}{cos\;\alpha}}+2}=\frac{2\;\tan\;\alpha\;-\;33\;\tan\;\alpha\;+\;}{3\;\tan\;\alpha\;+\;2}=\;\frac{2.3\;-\;3}{3.3\;+\;2}=\frac3{11}$ $P\;=\;\frac{2.{\displaystyle\frac{\sin\alpha}{cos\;\alpha}}-3}{3.{\displaystyle\frac{\sin\alpha}{cos\;\alpha}}+2}=\frac{2\;\tan\;\alpha\;-\;33\;\tan\;\alpha\;+\;}{3\;\tan\;\alpha\;+\;2}=\;\frac{2.3\;-\;3}{3.3\;+\;2}=\frac3{11}$

Vậy với α (0₀ < α < 180⁰) thỏa mãn tanα = 3 thì $P\;=\;\frac3{11}$ $P\;=\;\frac3{11}$

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ KNTT. Bài viết đã hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 KNTT. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 KNTT, Tiếng Anh lớp 10...