Giải Toán 10 Bài 18: Phương trình quy về phương trình bậc hai KNTT
Giải Toán 10 Bài 18 KNTT
VnDoc.com xin gửi tới bạn đọc bài viết Giải Toán 10 Bài 18: Phương trình quy về phương trình bậc hai KNTT. Mời các bạn cùng tham khảo chi tiết.
Bài 6.20 trang 27 SGK Toán 10 KNTT
Giải các phương trình sau:
\(a. \sqrt{3x^{2}-4x-1}=\sqrt{2x^{2}-4x+3}\)
\(b. \sqrt{x^{2}+2x-3}=\sqrt{-2x^{2}+5}\)
\(c. \sqrt{2x^{2}+3x-3}=\sqrt{-x^{2}-x+1}\)
\(d. \sqrt{-x^{2}+5x-4}=\sqrt{-2x^{2}+4x+3}\)
Gợi ý đáp án
\(a. \sqrt{3x^{2}-4x-1}=\sqrt{2x^{2}-4x+3}\)
Bình phương hai vế của phương trình ta được:
\(\Leftrightarrow x^{2}-4=0\)
\(\Leftrightarrow x = 2\) hoặc x = -2
Thử lại giá trị của x: đều thỏa mãn phương trình.
Vậy phương trình có nghiệm là x = 2 hoặc x = -2
\(b. \sqrt{x^{2}+2x-3}=\sqrt{-2x^{2}+5}\)
Bình phương hai vế của phương trình ta được:
\(x^{2}+2x-3=-2x^{2}+5\)
\(\Leftrightarrow 3x^{2}+2x-8=0\)
\(\Leftrightarrow x = -2\) hoặc \(x= \frac{4}{3}\)
Thử lại giá trị của x:
x = -2 không thỏa mãn phương trình,
\(x= \frac{4}{3}\) thỏa mãn phương trình.
Vậy nghiệm của phương trình là \(x= \frac{4}{3}.\)
\(c. \sqrt{2x^{2}+3x-3}=\sqrt{-x^{2}-x+1}\)
Bình phương hai vế của phương trình ta được:
\(2x^{2}+3x-3 = -x^{2}-x+1\)
\(\Leftrightarrow 3x^{2}+4x-4=0\)
\(\Leftrightarrow x = -2 hoặc x= \frac{2}{3}\)
Thử lại giá trị của x:
x = -2 không thỏa mãn phương trình,
\(x= \frac{2}{3}\) không thỏa mãn phương trình.
Vậy phương trình vô nghiệm.
\(d. \sqrt{-x^{2}+5x-4}=\sqrt{-2x^{2}+4x+3}\)
Bình phương hai vế của phương trình ta được:
\(-x^{2}+5x-4 = -2x^{2}+4x+3\)
\(\Leftrightarrow x^{2}+x-6=0\)
\(\Leftrightarrow x = 2\) hoặc x= -3
Thử lại giá trị của x:
x = 2 thỏa mãn phương trình,
x = -3 không thỏa mãn phương trình.
Vậy phương trình có nghiệm x = 2
Bài 6.21 trang 27 SGK Toán 10 KNTT
Giải các phương trình sau:
\(a. \sqrt{6x^{2}+13x+13}=2+4\)
\(b. \sqrt{2x^{2}+5x+3}=-3-x\)
\(c. \sqrt{3x^{2}-17x+23}=x-3\)
\(d. \sqrt{-x^{2}+2x+4}=x-2\)
Gợi ý đáp án
\(a. \sqrt{6x^{2}+13x+13}=2x+4\)
Bình phương hai vế của phương trình ta được:
\(6x^{2}+13x+13 = 4x^{2}+16x+16\)
\(\Leftrightarrow 2x^{2}-3x-3 = 0\)
\(\Leftrightarrow x=\frac{3+\sqrt{33}}{4} hoặc x=\frac{3-\sqrt{33}}{4}\)
Thử lại giá trị đều thỏa mãn.
Vậy phương trình có nghiệm \(x=\frac{3+\sqrt{33}}{4} hoặc x=\frac{3-\sqrt{33}}{4}\)
\(b. \sqrt{2x^{2}+5x+3}=-3-x\)
Bình phương hai vế của phương trình ta được:
\(2x^{2}+5x+3 = 9+6x+x^{2}\)
\(\Leftrightarrow x^{2}-x-6 = 0\)
\(\Leftrightarrow x=3\) hoặc x=-2
Thử lại giá trị đều không thỏa mãn.
Vậy phương trình vô nghiệm.
\(c. \sqrt{3x^{2}-17x+23}=x-3\)
Bình phương hai vế của phương trình ta được:
\(3x^{2}-17x+23 = x^{2}-6x+9\)
\(\Leftrightarrow 2x^{2}-11x+14 = 0\)
\(\Leftrightarrow x=2\) hoặc \(x=\frac{7}{2}\)
Thử lại các giá trị:
- x = 2 không thỏa mãn
- \(x=\frac{7}{2}\) thõa mãn.
Vậy phương trình có nghiệm \(x=\frac{7}{2}\)
\(d. \sqrt{-x^{2}+2x+4}=x-2\)
Bình phương hai vế của phương trình ta được:
\(-x^{2}+2x+4 = x^{2}-4x+4\)
\(\Leftrightarrow -2x^{2}+6x= 0\)
\(\Leftrightarrow x=0\) hoặc x=3
Thử lại giá trị:
- x = 0 không thỏa mãn
- x = 3 thỏa mãn
Vậy phương trình có nghiệm là x = 3.
Bài 6.22 trang 27 SGK Toán 10 KNTT
Cho tứ giác ABCD có AB \bot CD; AB = 2; BC = 13; CD = 8; DA = 5. Gọi H là giao điểm của AB và CD và đặt x = AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD.
Gợi ý đáp án
- Xét tam giác AHD vuông tại H có: \(HD = \sqrt{25-x^{2}}\) (áp dụng định lí Pytago).
- Xét tam giác BHC vuông tại H có: \(HB^{2}+HC^{2}=BC^{2}\)
\(=> (x+2)^{2}+\left ( \sqrt{25-x^{2}} +8\right )^{2}=13^{2}\)
\(\Leftrightarrow 4\sqrt{25-x^{2}}=19-x\)
Bình phương hai vế ta được:
\(16.(25-x^{2}) =361 - 38x +x^{2}\)
\(\Leftrightarrow 17x^{2}-38x-39=0\)
\(\Leftrightarrow x= 3\) hoặc \(x= \frac{-13}{17}\)
Thử lại phương trình và điều kiện x > 0, giá trị x= 3 thỏa mãn.
Vậy AH = x = 3.
- Diện tích tam giác HAD là: \(S_{HAD}=\frac{1}{2}AH.HD=6\)
- Diện tích tam giác HBC là: \(S_{HAD}=\frac{1}{2}HB.HC=36\)
Vậy diện tích tứ giác ABCD là: 36 - 6 = 30 (đơn vị diện tích).
Bài 6.23 trang 27 SGK Toán 10 KNTT
Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B, cách mình một đoạn 200 m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ Minh là 5 km/h, vận tốc xe đạp của Hùng là 15 km/h. Hãy xác định vị trí C trên lề đường để hai bạn gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết quả đến hàng phần mười).
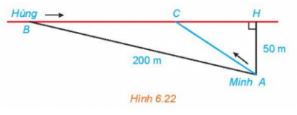
Gợi ý đáp án
Đặt CH = x (x >0)
Ta có: \(AC=\sqrt{x^{2}+50^{2}}=\sqrt{x^{2}+2500}\)
\(BH = \sqrt{200^{2}-50^{2}}=50\sqrt{15}\)
\(BC = BH - CH = 50\sqrt{15}-x\)
Vì hai bạn gặp nhau tại C, nên thời gian đi từ A đến C bằng thời gian đi từ B đến C, nên ta có phương trình:
\(\frac{50\sqrt{15}-x}{15}=\frac{\sqrt{x^{2}+2500}}{5}\)
\(\Leftrightarrow 50\sqrt{15}-x=3.\sqrt{x^{2}+2500}\)
Bình phương hai vế được:
\(37500-100\sqrt{15}.x+x^{2}=9.(x^{2}+2500)\)
\(\Leftrightarrow x\approx 25,4\) hoặc \(x\approx -73,8\)
Thử lại phương trình và điều kiện x >0 thì x = 25,4 thỏa mãn.
Vậy vị trí điểm C là cách H 1 khoảng 25,4 m.
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 18: Phương trình quy về phương trình bậc hai KNTT. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 10 KNTT. Mời các bạn cùng tham khảo thêm tài liệu học tập môn Ngữ văn 10 KNTT...
