Giải Toán 10 Bài 13: Các số đặc trưng đo xu thế trung tâm KNTT
Các số đặc trưng đo xu thế trung tâm
VnDoc.com xin gửi tới bạn đọc bài viết Giải Toán 10 Bài 13: Các số đặc trưng đo xu thế trung tâm KNTT. Mời các bạn cùng theo dõi bài viết dưới đây.
Bài 5.7 trang 82 SGK Toán 10 KNTT
Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:
a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:
9 8 15 8 20
b) Giá của một số loại giày (đơn vị nghìn đồng):
350 300 650 300 450 500 300 250
c) Số kênh được chiếu của một số hãng truyền hình cáp:
36 38 33 34 32 30 34 35
Gợi ý đáp án
a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:
9 8 15 8 20
Số trung bình: 
\(\overline X = \dfrac{{9 + 8 + 15 + 8 + 20}}{5} = 12\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
8 8 9 15 20
Ta có n=5 là số lẻ nên trung vị là 9.
Mốt: Ta thấy số 8 là số có tần số cao nhất (xuất hiện 2 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là \(9=> {Q_2} = 9.\)
+ Tìm \({Q_1}\)
Nửa số liệu bên trái là:
8 8
Trung vị của mẫu này là \(\dfrac{{8 + 8}}{2} = 8=>{Q_1} = 8\)
+ Tìm \({Q_3}\)
Nửa số liệu bên phải là:
15 20
Trung vị của mẫu này là \(\dfrac{{15 + 20}}{2} = 17,5=>{Q_3} = 17,5\)
Vậy số trung bình là 12, trung vị là 9 và mốt là 8, \({Q_1} = 8, {Q_3} = 17,5\)
b) Giá của một số loại giày (đơn vị nghìn đồng):
350 300 650 300 450 500 300 250
Số trung bình:\(\overline X ) = \dfrac{{350 + 300.3 + 650 + 450 + 500 + 250}}{8} = 387,5\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
250 300 300 300 350 450 500 650
Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.
Hai số chính giữa là 300 và 350
=> Trung vị là \(\dfrac{{300 + 350}}{2} = 325\)
Mốt: Ta thấy số 300 là số có tần số cao nhất (xuất hiện 3 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là 325=>\({Q_2} = 325.\)
+ Tìm \({Q_1}\)
Vì n chẵn nên nửa số liệu bên trái là:
250 300 300 300
Trung vị của mẫu này là \(\dfrac{{300 + 300}}{2} = 300=>{Q_1} = 300\)
+ Tìm \({Q_3}\)
Vì n chẵn nên nửa số liệu bên phải là:
350 450 500 650
Trung vị của mẫu này là \(\dfrac{{450 + 500}}{2} = 475=>{Q_3} = 475\)
Vậy số trung bình là 387,5, trung vị là 325 và mốt là 300,\({Q_1} = 300, {Q_3} = 475\)
c) Số kênh được chiếu của một số hãng truyền hình cáp:
36 38 33 34 32 30 34 35
Số trung bình: \(\overline X = \dfrac{{36 + 38 + 33 + 34.2 + 32 + 30 + 35}}{8} = 34\)
Trung vị:
Sắp xếp theo thứ tự không giảm:
30 32 33 34 34 35 36 38
Ta có n=8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.
Hai số chính giữa là 34 và 34
=> Trung vị là 34
Mốt: Ta thấy số 34 là số có tần số cao nhất (xuất hiện 2 lần)
Tứ phân vị:
+ Tìm \({Q_2}\)
Ta có trung vị là \(34=> {Q_2} = 34.\)
+ Tìm \({Q_1}\)
Vì n chẵn nên nửa số liệu bên trái là:
30 32 33 34
Trung vị của mẫu này là \(\dfrac{{32 + 33}}{2} = 32,5=>{Q_1} = 32,5\)
+ Tìm\({Q_3}\)
Vì n chẵn nên nửa số liệu bên phải là:
34 35 36 38
Trung vị của mẫu này là \(\dfrac{{35 + 36}}{2} = 35,5=>{Q_3} = 35,5\)
Vậy số trung bình là 34, trung vị là 34 và mốt là 34, \({Q_1} = 32,5, {Q_3} = 35,5\)
Chú ý
Nếu n chẵn thì nửa số liệu bên trái (phải) \({Q_2}\) phải chứa cả \({Q_2}\)
Bài 5.8 trang 82 SGK Toán 10 KNTT
Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích và tinh giá trị của số đặc trưng đó.
a) Số mặt trăng đã biết của các hành tinh:
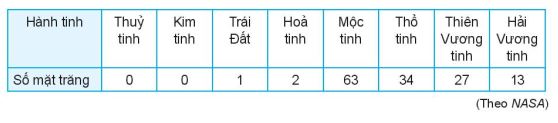
b) Số đường chuyền thành công trong một trận đấu của một số cầu thủ bóng đá:
32 24 20 14 23.
c) Chỉ số IQ của một nhóm học sinh:
| 80 | 102 | 83 | 103 | 108 | 94 | 110 | 106 | 104 | 100 |
d) Các sai số trong một phép đo: 10 15 18 15 14 13 42 15 12 14 42.
Gợi ý đáp án
a) Sắp xếp lại số liệu:
0 0 1 2 13 27 34 63
Trung vị là \(\dfrac{(2+13)}{2}=7,5.\)
Ta không chọn số trung bình vì số trung bình là 17,5 chênh lệch với 63 lớn. Mốt cũng thế.
b) Các số liệu bài cho không chênh lệch quá lớn với số trung bình nên ta chọn số trung bình.
Số đường truyền trung bình là: \(\dfrac{{32 + 24 + 20 + 14 + 23}}{5} = 22,6\)
c) Các số liệu bài cho không chênh lệch quá lớn với số trung bình nên ta chọn số trung bình.
IQ trung bình là \(\frac{{80 + {\kern 1pt} 102 + {\kern 1pt} 83 + {\kern 1pt} 103 + {\kern 1pt} 108 + {\kern 1pt} 94 + {\kern 1pt} 110 + {\kern 1pt} 106 + {\kern 1pt} 104 + {\kern 1pt} 100}}{{10}} = 99\)
d) Ta thấy có hai giá trị 42 chênh lệch lớn với các số còn lại nên ta chọn Mốt để đo xu thế trung tâm.
Mốt là 15 (tần số là 3).
Bài 5.9 trang 83 SGK Toán 10 KNTT
Số lượng học sinh giỏi Quốc gia năm học 2018-2019 của 10 trường Trung học phổ thông được cho như sau:
0 0 4 0 0 0 10 0 6 0.
a) Tìm số trung bình, mốt, các tứ phân vị của mẫu số liệu trên.
b) Giải thích tại sao tứ phân vị thứ nhất và trung vị trùng nhau.
Gợi ý đáp án
a) Sắp xếp theo thứ tự không giảm:
0 0 0 0 0 0 0 4 6 10
Số trung bình: \(\overline X = \dfrac{{0.7 + 4 + 6 + 10}}{{10}} = 2\)
Trung vị:\({Q_2} = 0\)
Tứ phân vị:
+ Nửa bên trái của \({Q_2}:\)
0 0 0 0 0
\(=>{Q_1} = 0\)
+ Nửa bên phải của \({Q_2}:\)
0 0 4 6 10
\(=>{Q_3} = 4\)
b) Tứ phân vị thứ nhất và trung vị trùng nhau vì mật độ của mẫu số liệu tập trung hết ở nửa trái của trung vị, mẫu số liệu bên trái có số liệu bằng 0 hết.
Bài 5.10 trang 83 SGK Toán 10 KNTT
Bảng sau đây cho biết số chỗ ngồi của một số sân vận động được sử dụng trong
Giải Bóng đá Vô địch Quốc gia Việt Nam năm 2018 (số liệu gần đúng).
Các giá trị số trung bình, trung vị, mốt bị ảnh hưởng thế nào nếu bỏ đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình?
Gợi ý đáp án
Sắp xếp lại mẫu số liệu:
20 120 20 120 21 315 23 405 37 546
Số trung bình:
\(\dfrac{{20120.2 + 21315 + 23405 + 37546}}{5} = 24501,2\)
Trung vị: 21 315
Mốt: 20 120
Nếu bỏ đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình thì số trung bình giảm, trung vị giảm và Mốt thì vẫn giữ nguyên.
Cụ thể: số trung bình là 21 240; trung vị là 20 717,5 và Mốt vẫn là 20 120
VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 13: Các số đặc trưng đo xu thế trung tâm KNTT. Bài viết đã hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 KNTT. Mời các bạn cùng tham khảo thêm tài liệu học tập môn Ngữ văn 10 KNTT...
