Giải Toán 10 Bài 3: Phương trình đường thẳng CD

Toán 10 Cánh diều tập 2

Giải Toán 10 Chương 7 Bài 3: Phương trình đường thẳng CD

Giải bài 1 trang 79 SGK Toán 10 Cánh diều tập 2
Giải bài 2 trang 79 SGK Toán 10 Cánh diều tập 2
Giải bài 3 trang 79 SGK Toán 10 Cánh diều tập 2
Giải bài 4 trang 80 SGK Toán 10 Cánh diều tập 2
Giải bài 5 trang 80 SGK Toán 10 Cánh diều tập 2
Giải bài 6 trang 80 SGK Toán 10 Cánh diều tập 2

Giải Toán 10 Bài 3: Phương trình đường thẳng CD được VnDoc.com sưu tầm và xin gửi tới bạn đọc. Bài viết hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 Cánh diều tập 2. Mời các bạn cùng theo dõi bài viết dưới đây.

Giải bài 1 trang 79 SGK Toán 10 Cánh diều tập 2

Lập phương trình tổng quát của đường thẳng Δ đi qua điểm A(-1; 2) và

a) Có vectơ pháp tuyến là $\vec{n}=(3,2)$ $\vec{n}=(3,2)$.

b) Có vectơ chỉ phương là $\vec{u} =(-2,3)$ $\vec{u} =(-2,3)$.

Lời giải:

a) Đường thẳng ∆ đi qua điểm A(-1; 2) nhận $\vec{n}=(3,2)$ $\vec{n}=(3,2)$ làm vectơ pháp tuyến.

Do đó, phương trình tổng quát của đường thẳng ∆ là: 3(x – (– 1)) + 2(y – 2) = 0 hay 3x + 2y – 1 = 0.

b) Đường thẳng ∆ có vectơ chỉ phương là $\vec{u} =(-2,3)$ $\vec{u} =(-2,3)$, suy ra ∆ có một vectơ pháp tuyến là $\vec{n}=(3,2)$ $\vec{n}=(3,2)$.

Đường thẳng ∆ đi qua điểm A(-1; 2) nhận $\vec{n}=(3,2)$ $\vec{n}=(3,2)$ làm vectơ pháp tuyến.

Do đó, phương trình tổng quát của đường thẳng ∆ là: 3(x – (– 1)) + 2(y – 2) = 0 hay 3x + 2y – 1 = 0.

Giải bài 2 trang 79 SGK Toán 10 Cánh diều tập 2

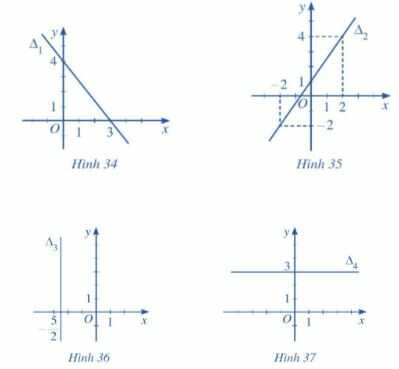
Lập phương trình mỗi đường thẳng trong các Hình 34, 35, 36, 37 sau đây:

Giải bài 2 trang 79 SGK Toán 10 tập 2 – Cánh diều

Lời giải:

* Quan sát Hình 34, ta thấy đường thẳng ∆1 đi qua hai điểm A(3; 0) và B(0; 4).

Ta có $\vec{AB}=(-3,4)$ $\vec{AB}=(-3,4)$.

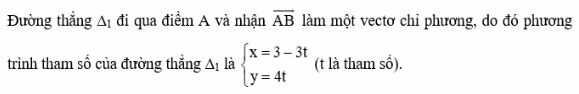
Giải bài 2 trang 79 SGK Toán 10 tập 2 – Cánh diều

* Quan sát Hình 35, ta thấy đường thẳng ∆2 đi qua hai điểm C(2; 4) và D(0; 1).

Ta có: $\vec{DC}=(2,3)$ $\vec{DC}=(2,3)$.

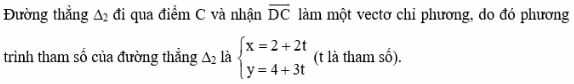
Giải bài 2 trang 79 SGK Toán 10 tập 2 – Cánh diều

* Quan sát Hình 36, ta thấy đường thẳng ∆3 song song với trục Oy và cắt trục Ox tại điểm $E=(-\frac{5}{2};0)$ $E=(-\frac{5}{2};0)$.

Do đó, phương trình đường thẳng ∆3 là $x=-\frac{5}{2}$ $x=-\frac{5}{2}$ hay 2x + 5 = 0.

* Quan sát Hình 37, ta thấy đường thẳng ∆4 song song với trục Ox và cắt trục Oy tại điểm F(0; 3).

Do đó, phương trình đường thẳng ∆4 là y = 3 hay y – 3 = 0.

Chú ý: Với các phương trình tham số của đường thẳng, ta có thể tùy chọn các điểm đi qua khác nhau và vectơ chỉ phương khác nhau để viết phương trình tham số.

Giải bài 3 trang 79 SGK Toán 10 Cánh diều tập 2

Cho đường thẳng d có phương trình tham số là:

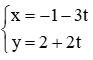
Giải bài 3 trang 79 SGK Toán 10 tập 2 – Cánh diều

a) Lập phương trình tổng quát của đường thẳng d.

b) Tìm tọa độ giao điểm của đường thẳng d lần lượt với các trục Ox, Oy.

c) Đường thẳng d có đi qua điểm M (-7; 5) hay không?

Lời giải:

a) Đường thẳng d có phương trình tham số là:

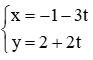
Giải bài 3 trang 79 SGK Toán 10 tập 2 – Cánh diều

Suy ra d có 1 vectơ chỉ phương là $\vec{u} =(-3,2)$ $\vec{u} =(-3,2)$, do đó d có 1 vectơ pháp tuyến là $\vec{n} =(2,3)$ $\vec{n} =(2,3)$

Ứng với t = 0, ta có

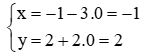
Giải bài 3 trang 79 SGK Toán 10 tập 2 – Cánh diều

Do đó điểm A(-1; 2) thuộc đường thẳng d.

Vậy đường thẳng d có phương trình tổng quát là 2(x + 1) + 3(y – 2) = 0 hay 2x + 3y – 4 = 0.

b) Gọi H, K lần lượt là giao điểm của đường thẳng d với các trục Ox và Oy.

Vì H thuộc Ox nên gọi tọa độ H(a; 0).

Do H thuộc d nên tọa độ điểm H thỏa mãn phương trình tổng quát của đường thẳng d, thay vào ta được: 2 . a + 3 . 0 – 4 = 0 ⇔ a = 2.

Vậy H(2; 0).

Vì điểm K thuộc Oy nên gọi tọa độ K(0; b).

Do K thuộc d nên tọa độ điểm K thỏa mãn phương trình tổng quát của đường thẳng d, thay vào ta được:

2 . 0 + 3 . b – 4 = 0 ⇔ $b=\frac{4}{3}$ $b=\frac{4}{3}$.

Vậy $K(0,\frac{4}{3} )$ $K(0,\frac{4}{3} )$.

Vậy tọa độ giao điểm của đường thẳng d lần lượt với các trục Ox, Oy lần lượt là các điểm H(2; 0) và $K(0,\frac{4}{3} )$ $K(0,\frac{4}{3} )$.

c) Thay tọa độ điểm M(-7; 5) vào phương trình tổng quát của đường thẳng d ta được:

2 . (-7) + 3 . 5 – 4 = 0 ⇔ – 3 = 0 (vô lý).

Vậy điểm M(-7; 5) không thuộc đường thẳng d hay đường thẳng d không đi qua điểm M(-7; 5).

Giải bài 4 trang 80 SGK Toán 10 Cánh diều tập 2

Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0.

a) Lập phương trình tham số của đường thẳng d.

b) Tìm tọa độ điểm M thuộc d sao cho OM = 5 với O là gốc tọa độ.

c) Tìm tọa độ điểm N thuộc d sao cho khoảng cách từ N đến trục hoành Ox là 3.

Lời giải:

a) Đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0.

Do đó d có 1 vectơ pháp tuyến là $\vec{n} =(1,-2)$ $\vec{n} =(1,-2)$, suy ra d có 1 vectơ chỉ phương là $\vec{u}=(2,1)$ $\vec{u}=(2,1)$

Cho y = 0, thay vào phương trình tổng quát của d ta được: x – 2 . 0 – 5 = 0 ⇔ x = 5.

Do đó, điểm A(5; 0) thuộc d.

Vậy phương trình tham số của đường thẳng d là

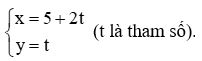
Giải bài 4 trang 80 SGK Toán 10 tập 2 – Cánh diều

Giải bài 5 trang 80 SGK Toán 10 Cánh diều tập 2

Cho tam giác ABC, biết A(1; 3); B(– 1; – 1); C(5; – 3). Lập phương trình tổng quát của:

a) Ba đường thẳng AB, BC, AC.

b) Đường trung trực cạnh AB.

c) Đường cao AH và đường trung tuyến AM của tam giác ABC.

Lời giải:

a) * Ta có: $\vec{AB}=(-2;-4)$ $\vec{AB}=(-2;-4)$.

Do đó đường thẳng AB nhận $\vec{u_{AB} }=-\frac{1}{2}\vec{AB}=-\frac{1}{2}(-2;-4)=(1;2)$ $\vec{u_{AB} }=-\frac{1}{2}\vec{AB}=-\frac{1}{2}(-2;-4)=(1;2)$ làm một vectơ chỉ phương.

Suy ra đường thẳng AB có một vectơ pháp tuyến là $\vec{n_{AB} }=(2;-1)$ $\vec{n_{AB} }=(2;-1)$.

Vậy phương trình tổng quát của đường thẳng AB là 2(x – 1) – 1(y – 3) = 0 hay 2x – y + 1 = 0.

* Ta có: $\vec{BC}=(6;-2)$ $\vec{BC}=(6;-2)$.

Do đó đường thẳng BC nhận $\vec{u_{BC} }=\frac{1}{2}\vec{BC}=\frac{1}{2}(6;-2)=(3;-1)$ $\vec{u_{BC} }=\frac{1}{2}\vec{BC}=\frac{1}{2}(6;-2)=(3;-1)$ làm một vectơ chỉ phương.

Suy ra đường thẳng BC có một vectơ pháp tuyến là $\vec{n_{BC} }=(1;3)$ $\vec{n_{BC} }=(1;3)$.

Vậy phương trình tổng quát của đường thẳng BC là 1(x + 1) + 3(y + 1) = 0 hay x + 3y + 4 = 0.

* Ta có: $\vec{AC}=(4;-6)$ $\vec{AC}=(4;-6)$.

Do đó đường thẳng AC nhận $\vec{u_{AC} }=\frac{1}{2}\vec{AC}=\frac{1}{2}(4;-6)=(2;-3)$ $\vec{u_{AC} }=\frac{1}{2}\vec{AC}=\frac{1}{2}(4;-6)=(2;-3)$ làm một vectơ chỉ phương.

Suy ra đường thẳng AC có một vectơ pháp tuyến là $\vec{n_{AC} }=(3;2)$ $\vec{n_{AC} }=(3;2)$.

Vậy phương trình tổng quát của đường thẳng AC là 3(x – 1) + 2(y – 3) = 0 hay 2x + 2y – 9 = 0.

b) Gọi N là trung điểm của AB, áp dụng công thức tọa độ trung điểm, suy ra tọa độ của điểm N là $x_{N}=\frac{1+(-1)}{2}=0$ $x_{N}=\frac{1+(-1)}{2}=0$; $y_{N}=\frac{3+(-1)}{2}=1$ $y_{N}=\frac{3+(-1)}{2}=1$ hay N(0; 1).

Đường trung trực cạnh AB vuông góc với AB nên nhận $\vec{u_{AB} }=(1;2)$ $\vec{u_{AB} }=(1;2)$ làm vectơ pháp tuyến.

Do đó đường trung trực cạnh AB đi qua điểm N(0; 1) và có 1 vectơ pháp tuyến là $\vec{n}=(1;2)$ $\vec{n}=(1;2)$.

Vậy phương trình tổng quát của đường trung trực cạnh AB là 1(x – 0) + 2(y – 1) = 0 hay x + 2y – 2 = 0.

c) * Đường cao AH của tam giác ABC vuông góc với cạnh BC.

Do đó đường cao AH đi qua điểm A(1; 3) và nhận $\vec{u_{BC} }=(3;-1)$ $\vec{u_{BC} }=(3;-1)$ làm vectơ pháp tuyến.

Vậy phương trình tổng quát của đường cao AH là 3(x – 1) – 1(y – 3) = 0 hay 3x – y = 0.

* AM là trung tuyến của tam giác ABC nên M là trung điểm của BC.

Suy ra tọa độ của điểm M là $x_{M}=\frac{(-1)+5}{2}=2$ $x_{M}=\frac{(-1)+5}{2}=2$; $y_{M}=\frac{(-1)+(-3)}{2}=-2$ $y_{M}=\frac{(-1)+(-3)}{2}=-2$ hay M(2; – 2).

Ta có: $\vec{AM}=(1;-5)$ $\vec{AM}=(1;-5)$.

Đường trung tuyến AM có một vectơ chỉ phương là $\vec{AM}=(1;-5)$ $\vec{AM}=(1;-5)$, do đó nó có một vectơ pháp tuyến là $\vec{n_{AM} }=(5;1)$ $\vec{n_{AM} }=(5;1)$.

Đường trung tuyến AM đi qua A(1; 3) và nhận $\vec{n_{AM} }=(5;1)$ $\vec{n_{AM} }=(5;1)$ làm vectơ pháp tuyến.

Vậy phương trình tổng quát của đường trung tuyến AM là 5(x – 1) + 1(y – 3) = 0 hay 5x + y – 8 = 0.

Giải bài 6 trang 80 SGK Toán 10 Cánh diều tập 2

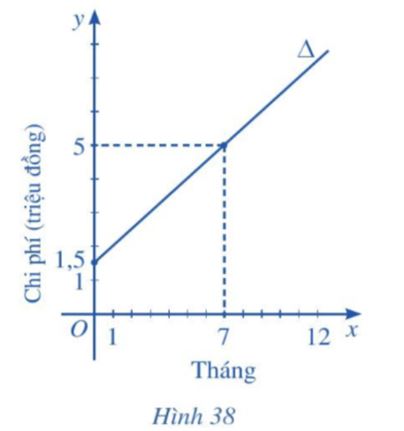
Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập. Đường thẳng Δ ở Hình 38 biểu thị tổng chi phí (đơn vị: triệu đồng) để tham gia một phòng tập thể dục theo thời gian tập của một người (đơn vị: tháng).

Giải bài 6 trang 80 SGK Toán 10 tập 2 – Cánh diều

a) Viết phương trình của đường thẳng Δ.

b) Giao điểm của đường thẳng Δ với trục tung trong tình huống này có ý nghĩa gì?

c) Tính tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng.

Lời giải:

a) Quan sát Hình 38, ta thấy đường thẳng ∆ đi qua 2 điểm A(0; 1,5) và B(7; 5).

Ta có: $\vec{AB}=(7;3;5)$ $\vec{AB}=(7;3;5)$.

Do đó, đường thẳng ∆ có một vectơ chỉ phương là $\vec{u}=\frac{2}{7} AB=\frac{2}{7} (7;3;5)=(2;1)$ $\vec{u}=\frac{2}{7} AB=\frac{2}{7} (7;3;5)=(2;1)$.

Vậy phương trình tham số của đường thẳng ∆ là

$\left\{\begin{matrix} x=7+2t \\ y=5+t \end{matrix}\right. (t là tham số)$ $\left\{\begin{matrix} x=7+2t \\ y=5+t \end{matrix}\right. (t là tham số)$

b) Giao điểm của đường thẳng ∆ với trục tung là điểm A(0; 1,5).

Giao điểm của đường thẳng Δ với trục tung trong tình huống này có ý nghĩa là: khoản phí tham gia ban đầu mà người tập phải trả là 1,5 triệu đồng.

c) Người đó tham gia phòng tập thể dục với thời gian là 12 tháng hay chính là x = 12, khi đó, tổng chi phí cần tìm chính là giá trị y tương ứng với x = 12.

Thay x = 12 vào phương trình tham số của đường thẳng ∆ ta được:

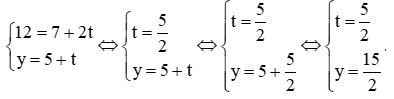
Giải bài 6 trang 80 SGK Toán 10 tập 2 – Cánh diều

Suy ra với x = 12 (tháng) thì $y=\frac{12}{5}=7.5$ $y=\frac{12}{5}=7.5$ (triệu đồng).

Vậy tổng chi phí mà người đo phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng là 7,5 triệu đồng.

---------------------

VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 3: Phương trình đường thẳng CD. Hi vọng qua đây bạn đọc có thêm nhiều tài liệu để học tập nhé. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 CD, Tiếng Anh 10...