VnDoc.com

Giải Toán 10 Bài 5: Tích của một số với một vectơ CD

Giải Toán 10 sách Cánh Diều

Bài trước

Tải về

Bài sau

Giải Toán 10 Bài 5 Chương 4 CD

Bài 1 trang 92 SGK Toán 10 CD
Bài 2 trang 92 SGK Toán 10 CD
Bài 3 trang 92 SGK Toán 10 CD
Bài 4 trang 92 SGK Toán 10 CD
Bài 5 trang 92 SGK Toán 10 CD
Bài 6 trang 92 SGK Toán 10 CD
Bài 7 trang 92 SGK Toán 10 CD

Giải Toán 10 Bài 5: Tích của một số với một vectơ CD được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây.

Bài 1 trang 92 SGK Toán 10 CD

Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?

A. $\overrightarrow {MN} = 2\overrightarrow {PQ}$ $\vec{M N} = 2 \vec{P Q}$

B. $\overrightarrow {MN} = 2\overrightarrow {NP}$ $\vec{M N} = 2 \vec{N P}$

C. $\overrightarrow {MN} = - 2\overrightarrow {PQ}$ $\vec{M N} = - 2 \vec{P Q}$

D. $\overrightarrow {MQ} = - 2\overrightarrow {NP}$ $\vec{M Q} = - 2 \vec{N P}$

Lời giải

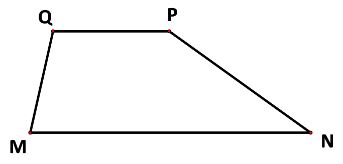
Giải Toán 10 Bài 5

Do MQ và PN không song song với nhau nên $\overrightarrow {MQ} \ne k\overrightarrow {NP}$ $\vec{M Q} \neq k \vec{N P}$ . Vậy loại B và D.

Ta có: $\overrightarrow {MN} ,\overrightarrow {PQ}$ $\vec{M N}, \vec{P Q}$ là hai vecto ngược hướng và $\left| {\overrightarrow {MN} } \right| = 2\left| {\overrightarrow {PQ} } \right|$ $| \vec{M N} | = 2 | \vec{P Q} |$

Suy ra $\overrightarrow {MN} = - 2\overrightarrow {PQ}$ $\vec{M N} = - 2 \vec{P Q}$

Vậy chọn C.

Bài 2 trang 92 SGK Toán 10 CD

Cho đoạn thẳng AB = 6 cm.

a) Xác định điểm C thỏa mãn $\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB}$ $\vec{A C} = \frac{1}{2} \vec{A B}$

b) Xác định điểm D thỏa mãn $\overrightarrow {AD} = - \frac{1}{2}\overrightarrow {AB}$ $\vec{A D} = - \frac{1}{2} \vec{A B}$

Lời giải

a) Ta có: $\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB}$ $\vec{A C} = \frac{1}{2} \vec{A B}$

$\Rightarrow$ $\Rightarrow$ Hai vecto $\overrightarrow {AB} ,\overrightarrow {AC}$ $\vec{A B}, \vec{A C}$ cùng hướng và $AC = \frac{1}{2}AB.$ $A C = \frac{1}{2} A B .$

Vậy C là trung điểm của AB.

b) Ta có: $\overrightarrow {AD} = - \frac{1}{2}\overrightarrow {AB} = - \overrightarrow {AC}$ $\vec{A D} = - \frac{1}{2} \vec{A B} = - \vec{A C}$

$\Rightarrow$ $\Rightarrow$ Hai vecto $\overrightarrow {AD} ,\overrightarrow {AC}$ $\vec{A D}, \vec{A C}$ ngược hướng và AD = AC.

Vậy A là trung điểm DC.

Bài 3 trang 92 SGK Toán 10 CD

Cho tam giác ABC có M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh:

a) $\overrightarrow {AP} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AN}$ $\vec{A P} + \frac{1}{2} \vec{B C} = \vec{A N}$

b) $\overrightarrow {BC} + 2\overrightarrow {MP} = \overrightarrow {BA}$ $\vec{B C} + 2 \vec{M P} = \vec{B A}$

Lời giải

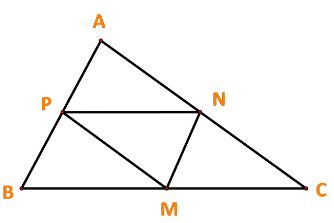
Giải Toán 10 Bài 5

a) Ta có: $\overrightarrow {BC} ,\overrightarrow {PN}$ $\vec{B C}, \vec{P N}$ là hai vecto cùng hướng và $\frac{1}{2}\left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {PN} } \right|$ $\frac{1}{2} | \vec{B C} | = | \vec{P N} |$

$\Rightarrow$ $\Rightarrow$ $\frac{1}{2}\overrightarrow {BC} = \overrightarrow {PN} \Rightarrow \overrightarrow {AP} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AP} + \overrightarrow {PN} = \overrightarrow {AN}$ $\frac{1}{2} \vec{B C} = \vec{P N} \Rightarrow \vec{A P} + \frac{1}{2} \vec{B C} = \vec{A P} + \vec{P N} = \vec{A N}$

b) Ta có: $\overrightarrow {MP} ,\overrightarrow {CA}$ $\vec{M P}, \vec{C A}$ là hai vecto cùng hướng và $2\left| {\overrightarrow {MP} } \right| = \left| {\overrightarrow {CA} } \right|$ $2 | \vec{M P} | = | \vec{C A} |$

$\Rightarrow 2\overrightarrow {MP} = \overrightarrow {CA} \Rightarrow \overrightarrow {BC} + 2\overrightarrow {MP} = \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow {BA}$ $\Rightarrow 2 \vec{M P} = \vec{C A} \Rightarrow \vec{B C} + 2 \vec{M P} = \vec{B C} + \vec{C A} = \vec{B A}$

Bài 4 trang 92 SGK Toán 10 CD

Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE = EC (Hình 62). Giả sử $\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AC} = \overrightarrow b$ $\vec{A B} = \vec{a}, \vec{A C} = \vec{b}$ . Biểu diễn các vecto $\overrightarrow {BC} ,\overrightarrow {BD} ,\overrightarrow {BE} ,\overrightarrow {AD} ,\overrightarrow {AE}$ $\vec{B C}, \vec{B D}, \vec{B E}, \vec{A D}, \vec{A E}$ theo $\overrightarrow a ,\overrightarrow b .$ $\vec{a}, \vec{b} .$

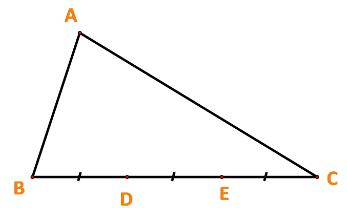
Giải Toán 10 Bài 5

Lời giải

Ta có: $\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {BC} = \overrightarrow b - \overrightarrow a$ $\vec{A B} + \vec{B C} = \vec{A C} \Leftrightarrow \vec{B C} = \vec{b} - \vec{a}$

Lại có: vecto $\overrightarrow {BD} ,\overrightarrow {BC}$ $\vec{B D}, \vec{B C}$ cùng hướng và $\left| {\overrightarrow {BD} } \right| = \frac{1}{3}\left| {\overrightarrow {BC} } \right|$ $| \vec{B D} | = \frac{1}{3} | \vec{B C} |$

$\Rightarrow \overrightarrow {BD} = \frac{1}{3}\overrightarrow {BC} = \frac{1}{3}(\overrightarrow b - \overrightarrow a )$ $\Rightarrow \vec{B D} = \frac{1}{3} \vec{B C} = \frac{1}{3} (\vec{b} - \vec{a})$

Tương tự: vecto $\overrightarrow {BE} ,\overrightarrow {BC}$ $\vec{B E}, \vec{B C}$ cùng hướng và $\left| {\overrightarrow {BE} } \right| = \frac{2}{3}\left| {\overrightarrow {BC} } \right|$ $| \vec{B E} | = \frac{2}{3} | \vec{B C} |$

$\Rightarrow \overrightarrow {BE} = \frac{2}{3}\overrightarrow {BC} = \frac{2}{3}(\overrightarrow b - \overrightarrow a )$ $\Rightarrow \vec{B E} = \frac{2}{3} \vec{B C} = \frac{2}{3} (\vec{b} - \vec{a})$

Ta có:

$\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \Leftrightarrow \overrightarrow {AD} = \overrightarrow a + \frac{1}{3}(\overrightarrow b - \overrightarrow a ) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b$ $\vec{A B} + \vec{B D} = \vec{A D} \Leftrightarrow \vec{A D} = \vec{a} + \frac{1}{3} (\vec{b} - \vec{a}) = \frac{2}{3} \vec{a} + \frac{1}{3} \vec{b}$

$\overrightarrow {AB} + \overrightarrow {BE} = \overrightarrow {AE} \Leftrightarrow \overrightarrow {AE} = \overrightarrow a + \frac{2}{3}(\overrightarrow b - \overrightarrow a ) = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b$ $\vec{A B} + \vec{B E} = \vec{A E} \Leftrightarrow \vec{A E} = \vec{a} + \frac{2}{3} (\vec{b} - \vec{a}) = \frac{1}{3} \vec{a} + \frac{2}{3} \vec{b}$

Bài 5 trang 92 SGK Toán 10 CD

Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm tam giác BCD. Chứng minh:

a) $\overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG}$ $\vec{E A} + \vec{E B} + \vec{E C} + \vec{E D} = 4 \vec{E G}$

b) $\overrightarrow {EA} = 4\overrightarrow {EG}$ $\vec{E A} = 4 \vec{E G}$

c) Điểm G thuộc đoạn thẳng AE và $\overrightarrow {AG} = \frac{3}{4}\overrightarrow {AE}$ $\vec{A G} = \frac{3}{4} \vec{A E}$

Lời giải

a) Ta có: $\overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD}$ $\vec{E A} + \vec{E B} + \vec{E C} + \vec{E D} = 4 \vec{E G} + \vec{G A} + \vec{G B} + \vec{G C} + \vec{G D}$

Mà: $\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM}$ $\vec{G A} + \vec{G B} = 2 \vec{G M}$ ; (do M là trung điểm của AB)

$\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN}$ $\vec{G C} + \vec{G D} = 2 \vec{G N}$ (do N là trung điểm của CD)

$\Rightarrow \overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG} + 2(\overrightarrow {GM} + \overrightarrow {GN} ) = 4\overrightarrow {EG}$ $\Rightarrow \vec{E A} + \vec{E B} + \vec{E C} + \vec{E D} = 4 \vec{E G} + 2 (\vec{G M} + \vec{G N}) = 4 \vec{E G}$ (do G là trung điểm của MN)

b) Vì E là trọng tâm tam giác BCD nên $\overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = \overrightarrow 0$ $\vec{E B} + \vec{E C} + \vec{E D} = \vec{0}$

Từ ý a ta suy ra $\overrightarrow {EA} = 4\overrightarrow {EG}$ $\vec{E A} = 4 \vec{E G}$

c) Ta có: $\overrightarrow {EA} = 4\overrightarrow {EG} \Leftrightarrow \overrightarrow {EA} = 4.(\overrightarrow {EA} + \overrightarrow {AG} ) \Leftrightarrow - 3\overrightarrow {EA} = 4\overrightarrow {AG}$ $\vec{E A} = 4 \vec{E G} \Leftrightarrow \vec{E A} = 4. (\vec{E A} + \vec{A G}) \Leftrightarrow - 3 \vec{E A} = 4 \vec{A G}$

$\Leftrightarrow 3\overrightarrow {AE} = 4\overrightarrow {AG}$ $\Leftrightarrow 3 \vec{A E} = 4 \vec{A G}$ hay $\overrightarrow {AG} = \frac{3}{4}\overrightarrow {AE}$ $\vec{A G} = \frac{3}{4} \vec{A E}$

Suy ra A, G, E thẳng hàng và $AG = \frac{3}{4}AE$ $A G = \frac{3}{4} A E$ nên G thuộc đoạn AE.

Bài 6 trang 92 SGK Toán 10 CD

Cho ABCD là hình bình hành. Đặt $\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b$ $\vec{A B} = \vec{a}, \vec{A D} = \vec{b}$ . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vecto $\overrightarrow {AG} ,\overrightarrow {CG}$ $\vec{A G}, \vec{C G}$ theo hai vecto $\overrightarrow a ,\overrightarrow b$ $\vec{a}, \vec{b}$ .

Lời giải

Gọi O là giao điểm của AC và BD.

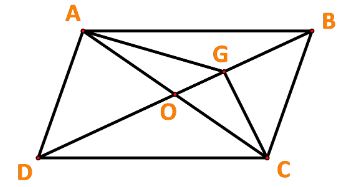
Giải Toán 10 Bài 5

Ta có:

$\begin{array}{l}\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow a + \overrightarrow {BG} ;\\\overrightarrow {CG} = \overrightarrow {CB} + \overrightarrow {BG} = \overrightarrow {DA} + \overrightarrow {BG} = - \overrightarrow b + \overrightarrow {BG} ;\end{array}(*)$ $\begin{array}{l} \vec{A G} = \vec{A B} + \vec{B G} = \vec{a} + \vec{B G}; \\ \vec{C G} = \vec{C B} + \vec{B G} = \vec{D A} + \vec{B G} = - \vec{b} + \vec{B G}; \end{array} (*)$

Lại có: $\overrightarrow {BD} =\overrightarrow {BA} + \overrightarrow {AD} = - \overrightarrow a + \overrightarrow b$ $\vec{B D} = \vec{B A} + \vec{A D} = - \vec{a} + \vec{b}$ .

$\overrightarrow {BG} ,\overrightarrow {BD}$ $\vec{B G}, \vec{B D}$ cùng phương và $\left| {\overrightarrow {BG} } \right| = \frac{2}{3}BO = \frac{1}{3}\left| {\overrightarrow {BD} } \right|$ $| \vec{B G} | = \frac{2}{3} B O = \frac{1}{3} | \vec{B D} |$

$\Rightarrow \overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD} = \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right)$ $\Rightarrow \vec{B G} = \frac{1}{3} \vec{B D} = \frac{1}{3} (- \vec{a} + \vec{b})$

Do đó $(*) \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AG} = \overrightarrow a + \overrightarrow {BG} = \overrightarrow a + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\\\overrightarrow {CG} = -\overrightarrow b + \overrightarrow {BG} = -\overrightarrow b + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b ;\end{array} \right.$ $(*) \Leftrightarrow {\begin{cases} \vec{A G} = \vec{a} + \vec{B G} = \vec{a} + \frac{1}{3} (- \vec{a} + \vec{b}) = \frac{2}{3} \vec{a} + \frac{1}{3} \vec{b}; \\ \vec{C G} = - \vec{b} + \vec{B G} = - \vec{b} + \frac{1}{3} (- \vec{a} + \vec{b}) = - \frac{1}{3} \vec{a} - \frac{2}{3} \vec{b}; \end{cases}$

Vậy $\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .$ $\vec{A G} = \frac{2}{3} \vec{a} + \frac{1}{3} \vec{b}; \vec{C G} = - \frac{1}{3} \vec{a} - \frac{2}{3} \vec{b} .$

Cách 2:

Gọi AE, CF là các trung tuyến trong tam giác ABC.

Giải Toán 10 Bài 5

Ta có:

$\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AE} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\overrightarrow {AB} + \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)} \right]$ $\vec{A G} = \frac{2}{3} \vec{A E} = \frac{2}{3} . \frac{1}{2} (\vec{A B} + \vec{A C}) = \frac{2}{3} . \frac{1}{2} [\vec{A B} + (\vec{A B} + \vec{A D})]$

$= \frac{1}{3}\left( {2\overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b$ $= \frac{1}{3} (2 \vec{a} + \vec{b}) = \frac{2}{3} \vec{a} + \frac{1}{3} \vec{b}$

$\overrightarrow {CG} = \frac{2}{3}\overrightarrow {CF} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\left( {\overrightarrow {CB} + \overrightarrow {CD} } \right) + \overrightarrow {CB} } \right]$ $\vec{C G} = \frac{2}{3} \vec{C F} = \frac{2}{3} . \frac{1}{2} (\vec{C A} + \vec{C B}) = \frac{2}{3} . \frac{1}{2} [(\vec{C B} + \vec{C D}) + \vec{C B}]$

$= \frac{1}{3}\left( {2\overrightarrow {CB} + \overrightarrow {CD} } \right) = \frac{1}{3}\left( { - 2\overrightarrow {AD} - \overrightarrow {AB} } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b$ $= \frac{1}{3} (2 \vec{C B} + \vec{C D}) = \frac{1}{3} (- 2 \vec{A D} - \vec{A B}) = - \frac{1}{3} \vec{a} - \frac{2}{3} \vec{b}$

Vậy $\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .$ $\vec{A G} = \frac{2}{3} \vec{a} + \frac{1}{3} \vec{b}; \vec{C G} = - \frac{1}{3} \vec{a} - \frac{2}{3} \vec{b} .$

Bài 7 trang 92 SGK Toán 10 CD

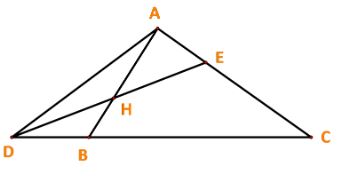
Cho tam giác ABC. Các điểm D, E, H thỏa mãn

$\overrightarrow {DB} = \frac{1}{3}\overrightarrow {BC} ,\;\overrightarrow {AE} = \frac{1}{3}\overrightarrow {AC} ,\;\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} .$ $\vec{D B} = \frac{1}{3} \vec{B C}, \vec{A E} = \frac{1}{3} \vec{A C}, \vec{A H} = \frac{2}{3} \vec{A B} .$

a) Biểu thị mỗi vecto $\overrightarrow {AD} ,\overrightarrow {DH} ,\overrightarrow {HE}$ $\vec{A D}, \vec{D H}, \vec{H E}$ theo hai vecto $\overrightarrow {AB} ,\overrightarrow {AC}$ $\vec{A B}, \vec{A C}$ .

b) Chứng minh D, E, H thẳng hàng.

Lời giải

Giải Toán 10 Bài 5

Dễ thấy: $\overrightarrow {BC} = \overrightarrow {BA} + \overrightarrow {AC} = - \overrightarrow {AB} + \overrightarrow {AC}$ $\vec{B C} = \vec{B A} + \vec{A C} = - \vec{A B} + \vec{A C}$

Ta có:

$+)\ \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BD} . Mà \overrightarrow {BD} = - \overrightarrow {DB} = - \frac{1}{3}\overrightarrow {BC}$ $+) \vec{A D} = \vec{A B} + \vec{B D} . M à \vec{B D} = - \vec{D B} = - \frac{1}{3} \vec{B C}$

$\Rightarrow \overrightarrow {AD} = \overrightarrow {AB} + \left( { - \frac{1}{3}} \right)( - \overrightarrow {AB} + \overrightarrow {AC} ) = \frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC}$ $\Rightarrow \vec{A D} = \vec{A B} + (- \frac{1}{3}) (- \vec{A B} + \vec{A C}) = \frac{4}{3} \vec{A B} - \frac{1}{3} \vec{A C}$

$+)\ \overrightarrow {DH} = \overrightarrow {DA} + \overrightarrow {AH} = - \overrightarrow {AD} + \overrightarrow {AH} .$ $+) \vec{D H} = \vec{D A} + \vec{A H} = - \vec{A D} + \vec{A H} .$

Mà $\overrightarrow {AD} = \frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} ;\;\;\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} .$ $\vec{A D} = \frac{4}{3} \vec{A B} - \frac{1}{3} \vec{A C}; \vec{A H} = \frac{2}{3} \vec{A B} .$

$\Rightarrow \overrightarrow {DH} = - \left( {\frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} } \right) + \frac{2}{3}\overrightarrow {AB} = - \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} .$ $\Rightarrow \vec{D H} = - (\frac{4}{3} \vec{A B} - \frac{1}{3} \vec{A C}) + \frac{2}{3} \vec{A B} = - \frac{2}{3} \vec{A B} + \frac{1}{3} \vec{A C} .$

$+)\ \overrightarrow {HE} = \overrightarrow {HA} + \overrightarrow {AE} = - \overrightarrow {AH} + \overrightarrow {AE}$ $+) \vec{H E} = \vec{H A} + \vec{A E} = - \vec{A H} + \vec{A E}$

Mà $\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} ;\;\overrightarrow {AE} = \frac{1}{3}\overrightarrow {AC}$ $\vec{A H} = \frac{2}{3} \vec{A B}; \vec{A E} = \frac{1}{3} \vec{A C}$

$\Rightarrow \overrightarrow {HE} = - \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} .$ $\Rightarrow \vec{H E} = - \frac{2}{3} \vec{A B} + \frac{1}{3} \vec{A C} .$

b)

Theo câu a, ta có: $\overrightarrow {DH} = \overrightarrow {HE} = - \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC}$ $\vec{D H} = \vec{H E} = - \frac{2}{3} \vec{A B} + \frac{1}{3} \vec{A C}$

$\Rightarrow$ $\Rightarrow$ Hai vecto $\overrightarrow {DH} ,\overrightarrow {HE}$ $\vec{D H}, \vec{H E}$ cùng phương.

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 5: Tích của một số với một vectơ CD. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán 10 CD. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 CD, Tiếng Anh 10...

Chia sẻ, đánh giá bài viết

1

182

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Linh An

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!