Giải Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác CD

Giải Toán 10 sách Cánh Diều

Giải Toán 10 Bài 2 Chương 4 CD

Bài 1 trang 77 SGK Toán 10 CD
Bà 2 trang 77 SGK Toán 10 CD
Bài 3 trang 77 SGK Toán 10 CD
Bài 4 trang 77 SGK Toán 10 CD
Bài 5 trang 77 SGK Toán 10 CD
Bài 6 trang 77 SGK Toán 10 CD
Bài 7 trang 77 SGK Toán 10 CD

Giải Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác CD được VnDoc.com sưu tầm và xin gửi tới bạn đọc. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

Bài 1 trang 77 SGK Toán 10 CD

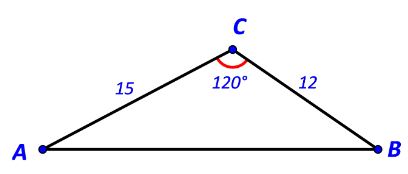
Cho tam giác ABC có $BC = 12,CA = 15,\widehat C = {120^o}.$ $BC = 12,CA = 15,\widehat C = {120^o}.$ Tính:

a) Độ dài cạnh AB.

b) Số đo các góc A, B.

c) Diện tích tam giác ABC.

Lời giải

Giải Toán 10 Bài 2 Chương 4

a) Áp dụng định lí cosin trong tam giác ABC ta có:

$A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C$ $A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C$

$\begin{array}{l} \Leftrightarrow A{B^2} = {15^2} + {12^2} - 2.15.12.\cos {120^o}\\ \Leftrightarrow A{B^2} = 549\\ \Leftrightarrow AB \approx 23,43\end{array}$ $\begin{array}{l} \Leftrightarrow A{B^2} = {15^2} + {12^2} - 2.15.12.\cos {120^o}\\ \Leftrightarrow A{B^2} = 549\\ \Leftrightarrow AB \approx 23,43\end{array}$

b) Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}$ $\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}$

$\Rightarrow \sin A = \frac{{BC}}{{AB}}.\sin C = \frac{{12}}{{23,43}}.\sin {120^o} \approx 0,44$ $\Rightarrow \sin A = \frac{{BC}}{{AB}}.\sin C = \frac{{12}}{{23,43}}.\sin {120^o} \approx 0,44$

$\Rightarrow \widehat A \approx {26^o} hoặc \widehat A \approx {154^o}$ $\Rightarrow \widehat A \approx {26^o} hoặc \widehat A \approx {154^o}$ (Loại)

Khi đó: $\widehat B = {180^o} - ({26^o} + {120^o}) = {34^o}$ $\widehat B = {180^o} - ({26^o} + {120^o}) = {34^o}$

c)

Diện tích tam giác ABC là: $S = \frac{1}{2}CA.CB.\sin C = \frac{1}{2}.15.12.\sin {120^o} = 45\sqrt 3$ $S = \frac{1}{2}CA.CB.\sin C = \frac{1}{2}.15.12.\sin {120^o} = 45\sqrt 3$

Bà 2 trang 77 SGK Toán 10 CD

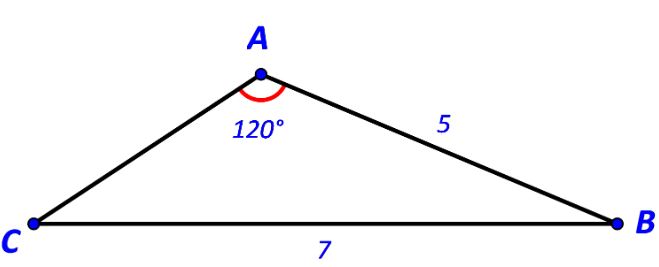
Cho tam giác ABC có $AB = 5,BC = 7,\widehat A = {120^o}$ $AB = 5,BC = 7,\widehat A = {120^o}$ . Tính độ dài cạnh AC.

Lời giải

Giải Toán 10 Bài 2 Chương 4

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}$ $\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}$

$\Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}$ $\Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}$

$\Rightarrow \widehat C \approx 38,{2^o}$ $\Rightarrow \widehat C \approx 38,{2^o}$ hoặc $\widehat C \approx 141,{8^o}$ $\widehat C \approx 141,{8^o}$ (Loại)

Ta có: $\widehat A = {120^o},\widehat C = 38,{2^o} \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}$ $\widehat A = {120^o},\widehat C = 38,{2^o} \Rightarrow \widehat B = {180^o} - \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}$

Áp dụng định lí cosin trong tam giác ABC ta có:

$\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}$ $\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} - 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}$

Vậy độ dài cạnh AC là 3.

Bài 3 trang 77 SGK Toán 10 CD

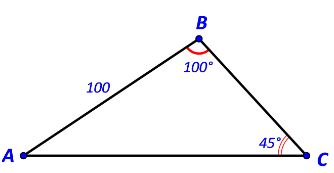
Cho tam giác ABC có $AB = 100,\widehat B = {100^o},\widehat C = {45^o}$ $AB = 100,\widehat B = {100^o},\widehat C = {45^o}$. Tính:

a) Độ dài các cạnh AC, BC

b) Diện tích tam giác ABC.

Lời giải

Giải Toán 10 Bài 2 Chương 4

a)

Ta có: $\widehat A = {180^o} - (\widehat B + \widehat C) \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}$ $\widehat A = {180^o} - (\widehat B + \widehat C) \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}$ $\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}$

$\Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.$ $\Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.$

b)

Diện tích tam giác ABC là: $S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.$ $S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.$

Bài 4 trang 77 SGK Toán 10 CD

Cho tam giác ABC có $AB = 12,AC = 15,BC = 20.$ Tính:

a) Số đo các góc A, B, C.

b) Diện tích tam giác ABC.

Lời giải

a) Áp dụng định lí cosin trong tam giác ABC, ta có:

$\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\;\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}$ $\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\;\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}$

Thay $a = BC = 20;\;b = AC = 15;\;c = AB = 12.$ $a = BC = 20;\;b = AC = 15;\;c = AB = 12.$

$\Rightarrow \cos A = - \frac{{31}}{{360}};\;\cos B = \frac{{319}}{{480}}$ $\Rightarrow \cos A = - \frac{{31}}{{360}};\;\cos B = \frac{{319}}{{480}}$

$\Rightarrow \widehat A = 94,{9^o};\;\widehat B = 48,{3^o}$ $\Rightarrow \widehat A = 94,{9^o};\;\widehat B = 48,{3^o}$

$\Rightarrow \widehat C = {180^o} - \left( {94,{9^o} + 48,{3^o}} \right) = 36,{8^o}$ $\Rightarrow \widehat C = {180^o} - \left( {94,{9^o} + 48,{3^o}} \right) = 36,{8^o}$

b)

Diện tích tam giác ABC là: $S = \frac{1}{2}.bc.\sin A = \frac{1}{2}.15.12.\sin 94,{9^o} \approx 89,7.$ $S = \frac{1}{2}.bc.\sin A = \frac{1}{2}.15.12.\sin 94,{9^o} \approx 89,7.$

Bài 5 trang 77 SGK Toán 10 CD

Tính độ dài cạnh AB trong mỗi trường hợp sau:

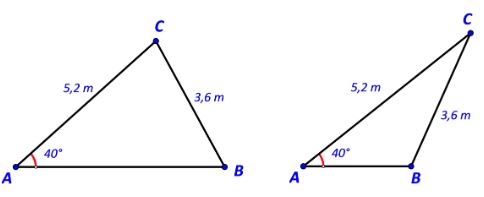
Giải Toán 10 Bài 2 Chương 4

Lời giải

Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}$ $\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}$

$\Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{5,2.\sin {{40}^o}}}{{3,6}} \approx 0,93$ $\Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{5,2.\sin {{40}^o}}}{{3,6}} \approx 0,93$

$\Rightarrow \widehat B \approx 68,{2^o}$ $\Rightarrow \widehat B \approx 68,{2^o}$ hoặc $\widehat B \approx 111,{8^o}$ $\widehat B \approx 111,{8^o}$

Trường hợp 1: $\widehat B \approx 68,{2^o}$ $\widehat B \approx 68,{2^o}$

Ta có: $\widehat C = {180^o} - (\widehat A + \widehat B) = {180^o} - ({40^o} + 68,{2^o}) = 71,{8^o}$ $\widehat C = {180^o} - (\widehat A + \widehat B) = {180^o} - ({40^o} + 68,{2^o}) = 71,{8^o}$

Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}$ $\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}$

$\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 71,{8^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 5,32$ $\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 71,{8^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 5,32$

Trường hợp 2: $\widehat B \approx 111,{8^o}$ $\widehat B \approx 111,{8^o}$

Ta có: $\widehat C = {180^o} - (\widehat A + \widehat B) = {180^o} - ({40^o} + 111,{8^o}) = 28,{2^o}$ $\widehat C = {180^o} - (\widehat A + \widehat B) = {180^o} - ({40^o} + 111,{8^o}) = 28,{2^o}$

Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}$ $\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}$

$\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 28,{2^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 2,65$ $\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 28,{2^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 2,65$

Vậy AB = 5,32 hoặc AB = 2,65.

Bài 6 trang 77 SGK Toán 10 CD

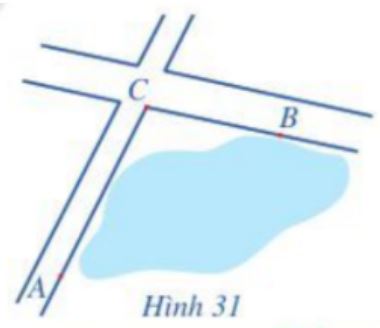
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và $\widehat {ACB} = {105^o}$ $\widehat {ACB} = {105^o}$ (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).

Giải Toán 10 Bài 2 Chương 4

Lời giải

Đổi: 1 km = 1000 m. Do đó AC = 1000 m.

Áp dụng định lí cosin trong tam giác ABC ta có:

$A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C$ $A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C$

$\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}$ $\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}$

Vậy khoảng cách AB là 1433,2 m.

Bài 7 trang 77 SGK Toán 10 CD

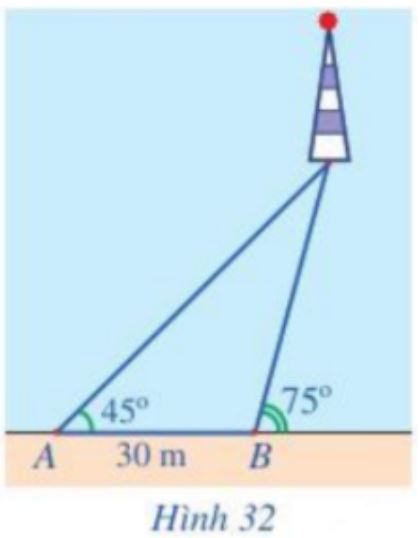
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là ${45^o}$ ${45^o}$ và ${75^o}$ ${75^o}$ . Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Giải Toán 10 Bài 2 Chương 4

Lời giải

Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.

Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.

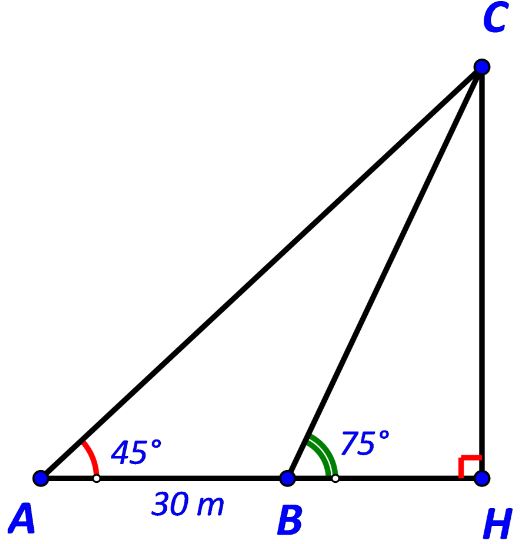
Giải Toán 10 Bài 2 Chương 4

Ta có: $\widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}$ $\widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}$ $\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}$

$\Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58$ $\Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58$

Tam giác ACH vuông tại H nên ta có:

$CH = \sin A.AC = \sin {45^o}.58 \approx 41$ $CH = \sin A.AC = \sin {45^o}.58 \approx 41$

Vậy ngọn hải đăng cách bờ biển 41 m.

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác CD. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán 10 CD. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 CD, Tiếng Anh 10 CD...

Chia sẻ, đánh giá bài viết

1

138

Bài trước

Bài sau