Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ CD

Giải Toán 10 sách Cánh Diều

Giải Toán 10 Bài 4 Chương 4 CD

Bài 1 trang 87 SGK Toán 10 CD
Bài 2 trang 87 SGK Toán 10 CD
Bài 3 trang 87 SGK Toán 10 CD
Bài 4 trang 87 SGK Toán 10 CD
Bài 5 trang 87 SGK Toán 10 CD
Bài 6 trang 87 SGK Toán 10 CD
Bài 7 trang 87 SGK Toán 10 CD
Bài 8 trang 87 SGK Toán 10 CD
Bài 9 trang 82 SGK Toán 10 CD

Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ CD được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

Bài 1 trang 87 SGK Toán 10 CD

Cho ba điểm M, N, P. Vecto $\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN}$ $\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN}$bằng vecto nào sau đây?

A. $\overrightarrow {PN}$ $\overrightarrow {PN}$

B. $\overrightarrow {PM}$ $\overrightarrow {PM}$

C. $\overrightarrow {MP}$ $\overrightarrow {MP}$

D. $\overrightarrow {NM}$ $\overrightarrow {NM}$

Lời giải

Vận dụng tính chất giao hoán ta có: $\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP}$ $\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP}$

Chọn C.

Bài 2 trang 87 SGK Toán 10 CD

Cho ba điểm D, E, G. Vecto $\overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} )$ $\overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} )$ bằng vecto nào sau đây?

A. $\overrightarrow {EG}$ $\overrightarrow {EG}$

B. $\overrightarrow {GE}$ $\overrightarrow {GE}$

C. $\overrightarrow {GD}$ $\overrightarrow {GD}$

D. $\overrightarrow {ED}$ $\overrightarrow {ED}$

Lời giải

Ta có: $\overrightarrow {GD} = - \overrightarrow {DG}$ $\overrightarrow {GD} = - \overrightarrow {DG}$

$\Rightarrow \overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} ) = \overrightarrow {DE} + \overrightarrow {GD}$ $\Rightarrow \overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} ) = \overrightarrow {DE} + \overrightarrow {GD}$

$\Rightarrow \overrightarrow v = \overrightarrow {GD} + \overrightarrow {DE} = \overrightarrow {GE}$ $\Rightarrow \overrightarrow v = \overrightarrow {GD} + \overrightarrow {DE} = \overrightarrow {GE}$ (tính chất giao hóan)

Chọn B.

Bài 3 trang 87 SGK Toán 10 CD

Cho bốn điểm A, B, C, D. Chứng minh:

a) $\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB}$ $\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB}$

b) $\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0$ $\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0$\

Lời giải

a)

$\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \\ \Leftrightarrow \overrightarrow {AB} - \overrightarrow {CB} = \overrightarrow {AD} - \overrightarrow {CD} \\ \Leftrightarrow \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} + \overrightarrow {DC} \\ \Leftrightarrow \overrightarrow {AC} = \overrightarrow {AC} \end{array}$ $\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \\ \Leftrightarrow \overrightarrow {AB} - \overrightarrow {CB} = \overrightarrow {AD} - \overrightarrow {CD} \\ \Leftrightarrow \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} + \overrightarrow {DC} \\ \Leftrightarrow \overrightarrow {AC} = \overrightarrow {AC} \end{array}$

(luôn đúng)

b) $\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0$ $\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0$

Ta có:

$\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = (\overrightarrow {AB} + \overrightarrow {BC} ) + (\overrightarrow {CD} + \overrightarrow {DA} )\\ = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \end{array}$ $\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = (\overrightarrow {AB} + \overrightarrow {BC} ) + (\overrightarrow {CD} + \overrightarrow {DA} )\\ = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \end{array}$

Chú ý khi giải

+) Hiệu hai vecto chung gốc: $\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB}$ $\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB}$(suy ra từ tổng $\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB}$ $\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB}$)

+) Với 4 điểm A, B, C, D bất kì ta có: $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow {AA} = \overrightarrow 0$ $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow {AA} = \overrightarrow 0$

Bài 4 trang 87 SGK Toán 10 CD

Cho hình hình hành ABCD, gọi O là giao điểm của AC và BD. Các khảng định sau đúng hay sai?

a) $|\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |$ $|\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |$

b) $\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {CB}$ $\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {CB}$

c) $\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD}$ $\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD}$

Lời giải

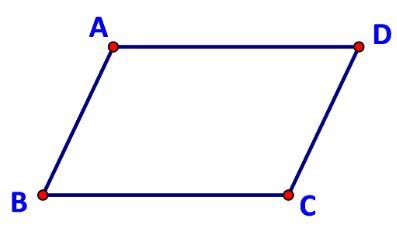
Giải Toán Bài 4 Chương 4

a) Theo quy tắc hình bình hành ta có: $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$ $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$

$\Rightarrow |\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |$ $\Rightarrow |\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |$

Vậy mệnh đề này đúng.

b) Ta có: $\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} \ne \overrightarrow {CB}$ $\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} \ne \overrightarrow {CB}$

Vậy mệnh đề này sai.

c) Ta có: $\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \Leftrightarrow \overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {OD} - \overrightarrow {OC} \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CD}$ $\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \Leftrightarrow \overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {OD} - \overrightarrow {OC} \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CD}$

(Đúng vì ABCD là hình bình hành)

Vậy mệnh đề này đúng.

Bài 5 trang 87 SGK Toán 10 CD

Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện cần và đủ để hai vecto $\overrightarrow {OA}$ $\overrightarrow {OA}$ và $\overrightarrow {OB}$ $\overrightarrow {OB}$ đối nhau.

Lời giải

Hai vecto $\overrightarrow {OA}$ $\overrightarrow {OA}$ và $\overrightarrow {OB}$ $\overrightarrow {OB}$ đối nhau $\Leftrightarrow$ $\Leftrightarrow$ hai tia OA, OB đối nhau và OA = OB.

$\Leftrightarrow O$ $\Leftrightarrow O$ là trung điểm của AB hay AB là đường kính của đường tròn (O).

Vậy điều kiện cần và đủ để hai vecto $\overrightarrow {OA}$ $\overrightarrow {OA}$ và $\overrightarrow {OB}$ $\overrightarrow {OB}$ đối nhau là AB là đường kính của đường tròn (O).

Bài 6 trang 87 SGK Toán 10 CD

Cho ABCD là hình bình hành. Chứng minh $\overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD}$ $\overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD}$ với mỗi điểm M trong mặt phẳng.

Lời giải

Ta có: $\overrightarrow {AM} = - \overrightarrow {MA} ,\;\overrightarrow {DM} = - \overrightarrow {MD}$ $\overrightarrow {AM} = - \overrightarrow {MA} ,\;\overrightarrow {DM} = - \overrightarrow {MD}$

$\Rightarrow \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MB} + \overrightarrow {AM} = \overrightarrow {AM} + \overrightarrow {MB} = \overrightarrow {AB}$ $\Rightarrow \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MB} + \overrightarrow {AM} = \overrightarrow {AM} + \overrightarrow {MB} = \overrightarrow {AB}$

Tương tự ta có: $\overrightarrow {MC} - \overrightarrow {MD} = \overrightarrow {MC} + \overrightarrow {DM} = \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {DC}$ $\overrightarrow {MC} - \overrightarrow {MD} = \overrightarrow {MC} + \overrightarrow {DM} = \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {DC}$

Mà $\overrightarrow {AB} = \overrightarrow {DC}$ $\overrightarrow {AB} = \overrightarrow {DC}$(do ABCD là hình bình hành)

$\Rightarrow \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD}$ $\Rightarrow \overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD}$(đpcm)

Bài 7 trang 87 SGK Toán 10 CD

Cho hình vuông ABCD có cạnh a. Tính độ dài các vecto sau:

a) $\overrightarrow {DA} + \overrightarrow {DC}$ $\overrightarrow {DA} + \overrightarrow {DC}$

b) $\overrightarrow {AB} - \overrightarrow {AD}$ $\overrightarrow {AB} - \overrightarrow {AD}$

c) $\overrightarrow {OA} + \overrightarrow {OB}$ $\overrightarrow {OA} + \overrightarrow {OB}$ với O là giao điểm của AC và BD.

Lời giải

a) Do ABCD cũng là một hình bình hành nên $\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB}$ $\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB}$

$\Rightarrow \;|\overrightarrow {DA} + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2$ $\Rightarrow \;|\overrightarrow {DA} + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2$

b) Ta có: $\overrightarrow {AD} + \overrightarrow {DB} = \overrightarrow {AB} \Rightarrow \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB}$ $\overrightarrow {AD} + \overrightarrow {DB} = \overrightarrow {AB} \Rightarrow \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB}$

$\Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2$ $\Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2$

c) Ta có: $\overrightarrow {DO} = \overrightarrow {OB}$ $\overrightarrow {DO} = \overrightarrow {OB}$

$\Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {DO} = \overrightarrow {DO} + \overrightarrow {OA} = \overrightarrow {DA}$ $\Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {DO} = \overrightarrow {DO} + \overrightarrow {OA} = \overrightarrow {DA}$

$\Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.$ $\Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.$

Bài 8 trang 87 SGK Toán 10 CD

Cho ba lực $\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}$ $\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}$ và $\overrightarrow {{F_3}} = \overrightarrow {OC}$ $\overrightarrow {{F_3}} = \overrightarrow {OC}$ cùng tác động vào một vật tại điểm O và vật đứng yên. Cho biết cường độ của $\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}}$ $\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}}$ đều là 120 N và $\widehat {AOB} = {120^o}$ $\widehat {AOB} = {120^o}$ . Tìm cường độ và hướng của lực $\overrightarrow {{F_3}}$ $\overrightarrow {{F_3}}$ .

Lời giải

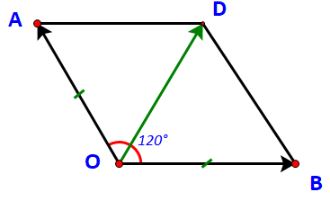
Giải Toán 10 Bài 4 Chương 4

Gọi D là đỉnh thứ tư của hình bình hành OADB.

Khi đó ta có: $\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD}$ $\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD}$

Ta có: OA = OB = 120 suy ra tứ giác OADB là hình thoi

$\Rightarrow \widehat {AOD} = \widehat {BOD} = \frac{{{{120}^o}}}{2} = {60^o}$ $\Rightarrow \widehat {AOD} = \widehat {BOD} = \frac{{{{120}^o}}}{2} = {60^o}$

$\Rightarrow \Delta AOD$ $\Rightarrow \Delta AOD$ đều (do OA = AD và $\widehat {AOD} = {60^o}$ $\widehat {AOD} = {60^o}$)

$\Rightarrow OD = OA = 120$ $\Rightarrow OD = OA = 120$

Mặt khác: Do vật đứng yên nên $\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \Leftrightarrow \;\overrightarrow {{F_3}} = - (\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} ) = - \overrightarrow {OD}$ $\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \Leftrightarrow \;\overrightarrow {{F_3}} = - (\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} ) = - \overrightarrow {OD}$

Suy ra vecto $\overrightarrow {OC}$ $\overrightarrow {OC}$ là vecto đối của vecto $\overrightarrow {OD}$ $\overrightarrow {OD}$

Lại có: $\widehat {COA} = {180^o} - \widehat {AOD} = {120^o}$ $\widehat {COA} = {180^o} - \widehat {AOD} = {120^o}$.Tương tự: $\widehat {COB} = {120^o}$ $\widehat {COB} = {120^o}$

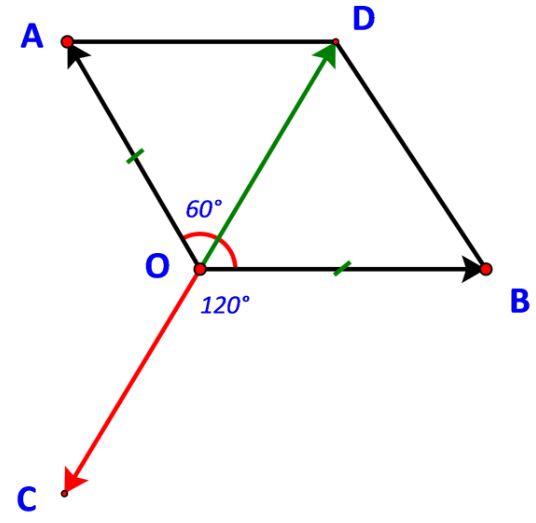
Toán 10 Bài 4 Chương 4

Vậy cường độ của lực $\overrightarrow {{F_3}}$ $\overrightarrow {{F_3}}$ là 120 N, tạo với lực $\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}}$ $\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}}$ góc ${120^o}.$ ${120^o}.$

Bài 9 trang 82 SGK Toán 10 CD

Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc là 10 km/h. Một chiếc ca nô chuyển động từ phía đông sang phía tây với vận tốc 40 km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông.

Lời giải

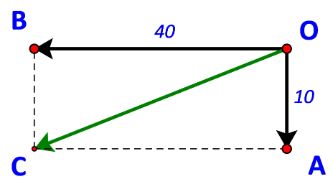
Giải Toán 10 Bài 4 Chương 4

Gọi O là vị trí của ca nô.

Vẽ $\overrightarrow {OA}$ $\overrightarrow {OA}$ là vận tốc dòng nước (chảy từ phía bắc xuống phía nam),

$\overrightarrow {OB}$ $\overrightarrow {OB}$ là vận tốc riêng của ca nô (chuyển động từ phía đông sang phía tây)

Khi đó vecto vận tốc của ca nô so với bờ sông là vecto $\overrightarrow {OA} + \overrightarrow {OB}$ $\overrightarrow {OA} + \overrightarrow {OB}$

Gọi C là đỉnh thứ tư của hình bình hành OACB, ta có: $\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB}$ $\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB}$

Xét tam giác OBC vuông tại B ta có:

BC = 40; BC = OA = 10.

$\Rightarrow OC = \sqrt {O{B^2} + B{C^2}} = 10\sqrt {17}$ $\Rightarrow OC = \sqrt {O{B^2} + B{C^2}} = 10\sqrt {17}$

Vậy vận tốc của ca nô so với bờ sông là $10\sqrt {17} km/h.$ $10\sqrt {17} km/h.$

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ CD. Bài viết đã hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 CD. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 CD, Tiếng Anh 10...

Chia sẻ, đánh giá bài viết

1

126

Bài trước

Bài sau