VnDoc.com

Giải Toán 10 Bài 3: Dấu của tam thức bậc hai CD

Giải Toán 10 sách Cánh Diều

Bài trước

Bài sau

Giải Toán 10 Bài 3 CD

Bài 1 trang 48 SGK Toán 10 CD
Bài 2 trang 48 SGK Toán 10 CD
Bài 3 trang 48 SGK Toán 10 CD
Bài 4 trang 48 SGK Toán 10 CD
Bài 5 trang 48 SGK Toán 10 CD

Giải Toán 10 Bài 3: Dấu của tam thức bậc hai CD được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo.

Bài 1 trang 48 SGK Toán 10 CD

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) ${x^2} - 2x - 3 = 0$ ${x^2} - 2x - 3 = 0$ khi và chỉ khi $x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)$ $x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)$

b) ${x^2} - 2x - 3 < 0$ ${x^2} - 2x - 3 < 0$ khi và chỉ khi $x \in \left[ { - 1;3} \right]$ $x \in \left[ { - 1;3} \right]$

Lời giải

a) Phương trình ${x^2} - 2x - 3 = 0$ ${x^2} - 2x - 3 = 0$ có 2 nghiệm phân biệt ${x_1} = - 1,{x_2} = 3$ ${x_1} = - 1,{x_2} = 3$

Có a = 1 > 0 nên $f\left( x \right) = {x^2} - 2x - 3 > 0$ $f\left( x \right) = {x^2} - 2x - 3 > 0$ khi và chỉ khi $x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)$ $x \in \left( { - \infty ; - 1} \right) \cup \left( {3; + \infty } \right)$

=> Phát biểu đúng.

b) Phương trình ${x^2} - 2x - 3 = 0$ ${x^2} - 2x - 3 = 0$ có 2 nghiệm phân biệt ${x_1} = - 1,{x_2} = 3$ ${x_1} = - 1,{x_2} = 3$

Có a = 1 > 0 nên $f\left( x \right) = {x^2} - 2x - 3 < 0$ $f\left( x \right) = {x^2} - 2x - 3 < 0$ khi và chỉ khi $x \in \left( { - 1;3} \right)$ $x \in \left( { - 1;3} \right)$

=> Phát biểu sai.

Bài 2 trang 48 SGK Toán 10 CD

Tìm nghiệm và lập bảng xét dấu của tam thức bậc hai $f\left( x \right)$ $f\left( x \right)$ với đồ thị được cho ở mỗi Hình 24a, 24b, 24c.

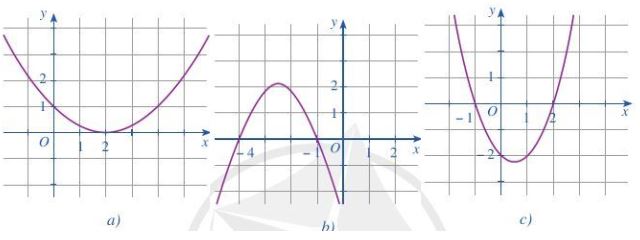
Giải Toán 10 Bài 3 CD

Hình 24a:

Ta thấy đồ thị cắt trục Ox tại điểm (2;0)

=> Phương trình $f\left( x \right) = 0$ $f\left( x \right) = 0$ có nghiệm duy nhất x = 2

Ta thấy đồ thị nằm trên trục hoành nên có bảng xét dấu:

Giải Toán 10 Bài 3

Hình 24b:

Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-4;0) và (-1;0)

=> Phương trình $f\left( x \right) = 0$ $f\left( x \right) = 0$ có 2 nghiệm phân biệt x = - 4,x = - 1

Trong các khoảng $\left( { - \infty ; - 4} \right)$ $\left( { - \infty ; - 4} \right)$ và $\left( { - 1; + \infty } \right)$ $\left( { - 1; + \infty } \right)$ thì đồ thị nằm dưới trục hoành nên $f\left( x \right) < 0$ $f\left( x \right) < 0$

Trong khoảng $\left( { - 4; - 1} \right)$ $\left( { - 4; - 1} \right)$ thì đồ thị nằm trên trục hoành nên $f\left( x \right) > 0$ $f\left( x \right) > 0$

Bảng xét dấu:

Giải Toán 10 Bài 3

Hình 24c:

Ta thấy đồ thị cắt trục Ox tại 2 điểm phân biệt (-1;0) và (2;0)

=> Phương trình $f\left( x \right) = 0$ $f\left( x \right) = 0$ có 2 nghiệm phân biệt $x = - 1,x = 2$

Trong các khoảng $\left( { - \infty ; - 1} \right)$ $\left( { - \infty ; - 1} \right)$ và $\left( {2; + \infty } \right)$ $\left( {2; + \infty } \right)$ thì đồ thị nằm trên trục hoành nên $f\left( x \right) > 0$ $f\left( x \right) > 0$

Trong khoảng $\left( { - 1;2} \right)$ $\left( { - 1;2} \right)$ thì đồ thị nằm dưới trục hoành nên $f\left( x \right) < 0$ $f\left( x \right) < 0$

Bảng xét dấu:

Giải Toán 10 Bài 3

Bài 3 trang 48 SGK Toán 10 CD

Xét dấu của mỗi tam thức bậc hai sau:

$a)\ f\left( x \right) = 3{x^2} - 4x + 1$ $a)\ f\left( x \right) = 3{x^2} - 4x + 1$

$b)\ f\left( x \right) = 9{x^2} + 6x + 1$ $b)\ f\left( x \right) = 9{x^2} + 6x + 1$

$c)\ f\left( x \right) = 2{x^2} - 3x + 10$ $c)\ f\left( x \right) = 2{x^2} - 3x + 10$

$d)\ f\left( x \right) = - 5{x^2} + 2x + 3$ $d)\ f\left( x \right) = - 5{x^2} + 2x + 3$

$e)\ f\left( x \right) = - 4{x^2} + 8x - 4$ $e)\ f\left( x \right) = - 4{x^2} + 8x - 4$

$g)\ f\left( x \right) = - 3{x^2} + 3x - 1$ $g)\ f\left( x \right) = - 3{x^2} + 3x - 1$

Lời giải

a) Ta có a = 3 > 0,b = - 4,c = 1

$\Delta$ $\Delta ' = {\left( { - 2} \right)^2} - 3.1 = 1 > 0$

$\Rightarrow f\left( x \right)$ $\Rightarrow f\left( x \right)$ có 2 nghiệm $x = \frac{1}{3},x = 1$ $x = \frac{1}{3},x = 1$. Khi đó:

$f\left( x \right) > 0$ $f\left( x \right) > 0$ với mọi x thuộc các khoảng $\left( { - \infty ;\frac{1}{3}} \right)$ $\left( { - \infty ;\frac{1}{3}} \right)$ và $\left( {1; + \infty } \right);$ $\left( {1; + \infty } \right);$

$f\left( x \right) < 0$ $f\left( x \right) < 0$ với mọi x thuộc các khoảng $\left( {\frac{1}{3};1} \right)$ $\left( {\frac{1}{3};1} \right)$

b) Ta có a = 9 > 0,b = 6,c = 1

$\Delta$ $\Delta ' = 0$

$\Rightarrow f\left( x \right)$ $\Rightarrow f\left( x \right)$ có 1 nghiệm $x = - \frac{1}{3}$ $x = - \frac{1}{3}$. Khi đó:

$f\left( x \right) > 0$ $f\left( x \right) > 0$ với mọi $x \in \mathbb{R}\backslash \left\{ { - \frac{1}{3}} \right\}$ $x \in \mathbb{R}\backslash \left\{ { - \frac{1}{3}} \right\}$

c) Ta có a = 2 > 0,b = - 3,c = 10

$\Delta = {\left( { - 3} \right)^2} - 4.2.10 = - 71 < 0$ $\Delta = {\left( { - 3} \right)^2} - 4.2.10 = - 71 < 0$

$\Rightarrow f\left( x \right) > 0\forall x \in \mathbb{R}$ $\Rightarrow f\left( x \right) > 0\forall x \in \mathbb{R}$

d) Ta có a = - 5 < 0,b = 2,c = 3

$\Delta$ $\Delta ' = {1^2} - \left( { - 5} \right).3 = 16 > 0$

$\Rightarrow f\left( x \right)$ $\Rightarrow f\left( x \right)$ có 2 nghiệm $x = \frac{{ - 3}}{5},x = 1$ $x = \frac{{ - 3}}{5},x = 1$. Khi đó:

$f\left( x \right) < 0$ $f\left( x \right) < 0$ với mọi x thuộc các khoảng $\left( { - \infty ; - \frac{3}{5}} \right)$ $\left( { - \infty ; - \frac{3}{5}} \right)$ và $\left( {1; + \infty } \right);$ $\left( {1; + \infty } \right);$

$f\left( x \right) > 0$ $f\left( x \right) > 0$ với mọi x thuộc các khoảng $\left( { - \frac{3}{5};1} \right)$ $\left( { - \frac{3}{5};1} \right)$

e) Ta có a = - 4 < 0,b = 8c = - 4

$\Delta$ $\Delta ' = 0$

$\Rightarrow f\left( x \right)$ $\Rightarrow f\left( x \right)$ có 1 nghiệm x = 2. Khi đó:

$f\left( x \right) < 0$ $f\left( x \right) < 0$ với mọi $x \in \mathbb{R}\backslash \left\{ 2 \right\}$ $x \in \mathbb{R}\backslash \left\{ 2 \right\}$

g) Ta có a = - 3 < 0,b = 3,c = - 1

$\Delta = {3^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = - 3 < 0$ $\Delta = {3^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = - 3 < 0$

$\Rightarrow f\left( x \right) < 0\forall x \in \mathbb{R}$ $\Rightarrow f\left( x \right) < 0\forall x \in \mathbb{R}$

Bài 4 trang 48 SGK Toán 10 CD

Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của một nhóm khách du lịch như sau:

50 khách đầu tiên có giá là 300 000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm 1 người, giá vé sẽ giảm 5 000 đồng/người cho toàn bộ hành khách.

a) Gọi x là số lượng khách từ người thứ 51 trở lên của nhóm. Biểu thị doanh thu theo x.

b) Số người của nhóm khách du lịch nhiều nhất là bao nhiêu thì công ty không bị lỗ? Biết rằng chi phí thực sự cho chuyến đi là 15 080 000 đồng.

Lời giải

a)

Do x là số lượng khách thứ 51 trở lên nên x>0.

Cứ thêm 1 người thì giá còn (300000-5 000.1) đồng/người cho toàn bộ hành khách.

Thêm x người thì giá còn (300 000-5 000.x) đồng/người cho toàn bộ hành khách.

Doanh thu theo $x: \left( {50 + x} \right).\left( {300000 - 5000x} \right) (VNĐ)$ $x: \left( {50 + x} \right).\left( {300000 - 5000x} \right) (VNĐ)$

b) Do chi phí thực sự cho chuyến đi là 15 080 000 đồng nên để công ty không bị lỗ thì doanh thu phải lớn hơn hoặc bằng 15 080 000 đồng

Khi đó:

$\begin{array}{l}\left( {50 + x} \right).\left( {300000 - 5000x} \right) \ge 15080000\\ \Leftrightarrow \left( {50 + x} \right).5000.\left( {60 - x} \right) \ge 15080000\\ \Leftrightarrow \left( {x + 50} \right)\left( {60 - x} \right) \ge 3016\\ \Leftrightarrow - {x^2} + 10x + 3000 \ge 3016\\ \Leftrightarrow - {x^2} + 10x - 16 \ge 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {8 - x} \right) \ge 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 2 \le x \le 8\end{array}$ $\begin{array}{l}\left( {50 + x} \right).\left( {300000 - 5000x} \right) \ge 15080000\\ \Leftrightarrow \left( {50 + x} \right).5000.\left( {60 - x} \right) \ge 15080000\\ \Leftrightarrow \left( {x + 50} \right)\left( {60 - x} \right) \ge 3016\\ \Leftrightarrow - {x^2} + 10x + 3000 \ge 3016\\ \Leftrightarrow - {x^2} + 10x - 16 \ge 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {8 - x} \right) \ge 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 2 \le x \le 8\end{array}$

Vậy số người của nhóm du khách nhiều nhất là 58 người.

Bài 5 trang 48 SGK Toán 10 CD

Bộ phận nghiên cứu thị trường của một xí nghiệp xác định tổng chi phí để sản xuất

Q sản phẩm là ${Q^2} + 180Q + 140000$ ${Q^2} + 180Q + 140000$ (nghìn đồng). Giả sử giá mỗi sản phẩm bán ra

thị trường là 1 200 nghìn đồng.

a) Xác định lợi nhuận xí nghiệp thu được sau khi bán hết Q sản phẩm đó, biết rằng lợi nhuận là hiệu của doanh thu trừ đi tổng chi phí để sản xuất.

b) Xí nghiệp sản xuất bao nhiều sản phẩm thì hoà vốn?

c) Xí nghiệp cần sản xuất số sản phẩm là bao nhiêu để không bị lỗ?

Lời giải

a) Doanh thu khi bán hết Q sản phẩm là 1200Q (nghìn đồng)

Lợi nhuận bán hết Q sản phẩm là:

$\begin{array}{l}1200Q - \left( {{Q^2} + 180Q + 140000} \right)\\ = - {Q^2} + 1020Q - 140000\end{array}$ $\begin{array}{l}1200Q - \left( {{Q^2} + 180Q + 140000} \right)\\ = - {Q^2} + 1020Q - 140000\end{array}$

b)

Để xí nghiệp hòa vốn thì: Lợi nhuận bằng 0.

$\begin{array}{l} \Leftrightarrow - {Q^2} + 1020Q - 140000 = 0\\ \Leftrightarrow \left[ \begin{array}{l}Q \approx 857\\Q \approx 163\end{array} \right.\end{array}$ $\begin{array}{l} \Leftrightarrow - {Q^2} + 1020Q - 140000 = 0\\ \Leftrightarrow \left[ \begin{array}{l}Q \approx 857\\Q \approx 163\end{array} \right.\end{array}$

Vậy xí nghiệp sản xuất 163 sản phẩm hoặc 857 sản phẩm thì hòa vốn.

c) Để không bị lỗ thì lợi nhuận lớn hơn hoặc bằng 0.

Khi đó:

$\begin{array}{l} - {Q^2} + 1020Q - 140000 \ge 0\\ \Leftrightarrow 163,45 \le Q \le 857,55\\ \Rightarrow 164 \le Q \le 857\end{array}$ $\begin{array}{l} - {Q^2} + 1020Q - 140000 \ge 0\\ \Leftrightarrow 163,45 \le Q \le 857,55\\ \Rightarrow 164 \le Q \le 857\end{array}$

Vậy để không bị lỗ thì xí nghiệp cần sản xuất số sản phẩm nằm trong khoảng 164 đến 857.

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 3: Dấu của tam thức bậc hai CD. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán 10 CD. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 CD, Tiếng Anh lớp 10...