Giải Toán 10 Bài 3: Tích của một số với một vectơ CTST

Giải Toán 10 Tập 1 sách CTST

Tích của một số với một vectơ

Bài 1 trang 97 SGK Toán 10 CTST
Bài 2 trang 97 SGK Toán 10 CTST
Bài 3 trang 97 SGK Toán 10 CTST
Bài 4 trang 97 SGK Toán 10 CTST
Bài 5 trang 97 SGK Toán 10 CTST
Bài 6 trang 97 SGK Toán 10 CTST
Bài 7 trang 97 SGK Toán 10 CTST

Giải Toán 10 Bài 3: Tích của một số với một vectơ CTST được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây nhé.

Bài 1 trang 97 SGK Toán 10 CTST

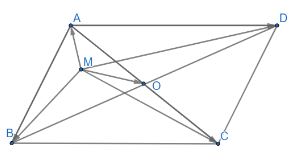
Cho hình bình hành ABCD D có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

$a) \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO}$ $a) \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO}$

$b) \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 2\overrightarrow {AC}$ $b) \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 2\overrightarrow {AC}$

Gợi ý đáp án

$\Leftrightarrow \overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {MO} + \overrightarrow {OB} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OD} = 4\overrightarrow {MO}$ $\Leftrightarrow \overrightarrow {MO} + \overrightarrow {OA} + \overrightarrow {MO} + \overrightarrow {OB} + \overrightarrow {MO} + \overrightarrow {OC} + \overrightarrow {MO} + \overrightarrow {OD} = 4\overrightarrow {MO}$

a) $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO}$ $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO}$

$\Leftrightarrow 4\overrightarrow {MO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) = 4\overrightarrow {MO}$ $\Leftrightarrow 4\overrightarrow {MO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right) = 4\overrightarrow {MO}$

$\Leftrightarrow 4\overrightarrow {MO} + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MO} \\ \Leftrightarrow 4\overrightarrow {MO} = 4\overrightarrow {MO}$ $\Leftrightarrow 4\overrightarrow {MO} + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MO} \\ \Leftrightarrow 4\overrightarrow {MO} = 4\overrightarrow {MO}$ (luôn đúng)

(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)

b) ABCD là hình bình hành nên ta có $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$ $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$

Suy ra $\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AC} = \overrightarrow {AC} + \overrightarrow {AC} = 2\overrightarrow {AC}$ $\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {AC} = \overrightarrow {AC} + \overrightarrow {AC} = 2\overrightarrow {AC}$(đpcm)

Bài 2 trang 97 SGK Toán 10 CTST

Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng

$a) \overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN}$ $a) \overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN}$

$b) \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD}$ $b) \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD}$

Gợi ý đáp án

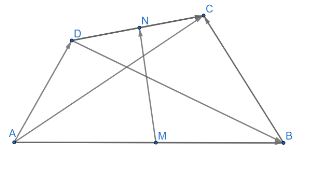
$a) \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right)$ $a) \overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right)$

$= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN}$ $= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN}$(đpcm)

b) $\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD}$ $\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD}$

$\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND}$ $\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND}$

$\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN}$ $\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN}$

Mặt khác ta có: $\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN}$ $\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN}$

Suy ra $\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD}$ $\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD}$

Bài 3 trang 97 SGK Toán 10 CTST

Cho hai điểm phân biệt A và B. Xác định điểm M sao cho $\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0$ $\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0$

Gợi ý đáp án

$\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} = - 4\overrightarrow {MB} \Rightarrow \frac{{MA}}{{MB}}$ $\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} = - 4\overrightarrow {MB} \Rightarrow \frac{{MA}}{{MB}}$

$= \frac{{\left| {\overrightarrow {MA} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = \frac{{\left| { - 4\overrightarrow {MB} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = 4 và hai vectơ \overrightarrow {MA} ,\overrightarrow {MB}$ $= \frac{{\left| {\overrightarrow {MA} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = \frac{{\left| { - 4\overrightarrow {MB} } \right|}}{{\left| {\overrightarrow {MB} } \right|}} = 4 và hai vectơ \overrightarrow {MA} ,\overrightarrow {MB}$ ngược hướng

Suy ra M nằm giữa AB sao cho $\frac{{MA}}{{MB}} = 4$ $\frac{{MA}}{{MB}} = 4$

Bài 4 trang 97 SGK Toán 10 CTST

Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MG}$ $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MG}$

Gợi ý đáp án

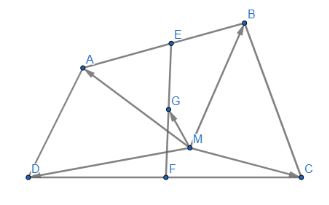
$\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EA} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FC} } \right)\\ + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FD} } \right)\end{array}$ $\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EA} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GE} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FC} } \right)\\ + \left( {\overrightarrow {MG} + \overrightarrow {GF} + \overrightarrow {FD} } \right)\end{array}$

$= \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} \overrightarrow { + MG} } \right) + 2\left( {\overrightarrow {GE} + \overrightarrow {GF} } \right) + \left( {\overrightarrow {EA} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {FC} + \overrightarrow {FD} } \right)$ $= \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} \overrightarrow { + MG} } \right) + 2\left( {\overrightarrow {GE} + \overrightarrow {GF} } \right) + \left( {\overrightarrow {EA} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {FC} + \overrightarrow {FD} } \right)$

$= 4\overrightarrow {MG} + 2.\overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MG}$ $= 4\overrightarrow {MG} + 2.\overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = 4\overrightarrow {MG}$(đpcm)

Bài 5 trang 97 SGK Toán 10 CTST

Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc \overrightarrow b của máy bay B theo vectơ vận tốc $\overrightarrow a$ $\overrightarrow a$ của máy bay A

Gợi ý đáp án

Vecto $\overrightarrow a ,\;\overrightarrow b$ $\overrightarrow a ,\;\overrightarrow b$ là vecto vận tốc của máy bay A và máy bay b.

Do đó $\left| {\overrightarrow a } \right|,\;\left| {\overrightarrow b } \right|$ $\left| {\overrightarrow a } \right|,\;\left| {\overrightarrow b } \right|$ lần lượt là độ lớn của vecto vận tốc tương ứng.

Ta có: $\left| {\overrightarrow a } \right| = 600,\;\left| {\overrightarrow b } \right| = 800$ $\left| {\overrightarrow a } \right| = 600,\;\left| {\overrightarrow b } \right| = 800$

$\Rightarrow \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{800}}{{600}} = \frac{4}{3}$ $\Rightarrow \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{800}}{{600}} = \frac{4}{3}$

Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó $\overrightarrow b = - \frac{4}{3}\overrightarrow a$ $\overrightarrow b = - \frac{4}{3}\overrightarrow a$

Bài 6 trang 97 SGK Toán 10 CTST

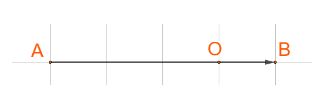
Cho 2 điểm phân biệt A và B

a) Xác định điểm O sao cho $\overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0$ $\overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0$

b) Chứng minh rằng với mọi điểm M, ta có $\overrightarrow {MA} + 3\overrightarrow {MB} = 4\overrightarrow {MO}$ $\overrightarrow {MA} + 3\overrightarrow {MB} = 4\overrightarrow {MO}$

Gợi ý đáp án

$a) \overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0$ $a) \overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0$

$\begin{array}{l} \overrightarrow {OA} + 3\overrightarrow {OB} = \vec 0\\ \Leftrightarrow \overrightarrow {OB} + \overrightarrow {BA} + 3\overrightarrow {OB} = \vec 0\\ \Leftrightarrow \overrightarrow {OB} + 3\overrightarrow {OB} = - \overrightarrow {BA} \\ \Leftrightarrow 4\overrightarrow {OB} = \overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {OB} = \frac{1}{4}\overrightarrow {AB} \end{array}$ $\begin{array}{l} \overrightarrow {OA} + 3\overrightarrow {OB} = \vec 0\\ \Leftrightarrow \overrightarrow {OB} + \overrightarrow {BA} + 3\overrightarrow {OB} = \vec 0\\ \Leftrightarrow \overrightarrow {OB} + 3\overrightarrow {OB} = - \overrightarrow {BA} \\ \Leftrightarrow 4\overrightarrow {OB} = \overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {OB} = \frac{1}{4}\overrightarrow {AB} \end{array}$

Vậy O thuộc đoạn AB sao cho $OB = \frac{1}{4}AB$ $OB = \frac{1}{4}AB$

b) Ta có:

Giải Toán 10 Bài 3 CTST

$\begin{array}{l} \overrightarrow {MA} + 3\overrightarrow {MB} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right)\\ = \left( {\overrightarrow {MO} + 3\overrightarrow {MO} } \right) + \left( {\overrightarrow {OA} + 3\overrightarrow {OB} } \right)\\ = 4\overrightarrow {MO} + \overrightarrow 0 = 4\overrightarrow {MO} . (đpcm) \end{array}$ $\begin{array}{l} \overrightarrow {MA} + 3\overrightarrow {MB} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right)\\ = \left( {\overrightarrow {MO} + 3\overrightarrow {MO} } \right) + \left( {\overrightarrow {OA} + 3\overrightarrow {OB} } \right)\\ = 4\overrightarrow {MO} + \overrightarrow 0 = 4\overrightarrow {MO} . (đpcm) \end{array}$

Bài 7 trang 97 SGK Toán 10 CTST

Cho tam giác ABC

a) Xác định các điểm M, N, P thỏa mãn: $\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} ,\overrightarrow {AN} = 3\overrightarrow {NB} ,\overrightarrow {CP} = \overrightarrow {PA}$ $\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} ,\overrightarrow {AN} = 3\overrightarrow {NB} ,\overrightarrow {CP} = \overrightarrow {PA}$

b) Biểu thị mỗi vectơ $\overrightarrow {MN} ,\overrightarrow {MP}$ $\overrightarrow {MN} ,\overrightarrow {MP}$ theo hai vectơ $\overrightarrow {BC} ,\overrightarrow {BA}$ $\overrightarrow {BC} ,\overrightarrow {BA}$

c) Chứng minh ba điểm M, N, P thẳng hàng

Gợi ý đáp án

a) Ta có:

+) $\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} \Rightarrow \overrightarrow {MB}$ $\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} \Rightarrow \overrightarrow {MB}$ và $\overrightarrow {BC}$ $\overrightarrow {BC}$ cùng hướng; tỉ số độ dài $\frac{{BC}}{{MB}} = 2$ $\frac{{BC}}{{MB}} = 2$

$\Rightarrow M$ $\Rightarrow M$ nằm ngoài đoạn thẳng BC sao cho $MB = \frac{1}{2}BC$ $MB = \frac{1}{2}BC$

$+) {\overrightarrow {AN} = 3\overrightarrow {NB} \Rightarrow \overrightarrow {AB} + \overrightarrow {BN} = 3\overrightarrow {NB} \Rightarrow 4\overrightarrow {NB} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {NB} = \frac{1}{4}\overrightarrow {AB} }$ $+) {\overrightarrow {AN} = 3\overrightarrow {NB} \Rightarrow \overrightarrow {AB} + \overrightarrow {BN} = 3\overrightarrow {NB} \Rightarrow 4\overrightarrow {NB} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {NB} = \frac{1}{4}\overrightarrow {AB} }$

$\Rightarrow N$ $\Rightarrow N$ thuộc đoạn thẳng AB và $NB=\frac{{1}}{{4}} AB$ $NB=\frac{{1}}{{4}} AB$

$+) \overrightarrow {CP} = \overrightarrow {PA} \Leftrightarrow \overrightarrow {PC} + \overrightarrow {PA} = \overrightarrow 0$ $+) \overrightarrow {CP} = \overrightarrow {PA} \Leftrightarrow \overrightarrow {PC} + \overrightarrow {PA} = \overrightarrow 0$

$\Rightarrow P$ $\Rightarrow P$ là trung điểm của CA

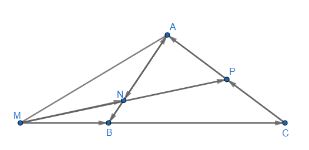
$b) \overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA}$ $b) \overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA}$

$\begin{array}{l}\overrightarrow {MP} = \overrightarrow {MC} + \overrightarrow {CP} = \overrightarrow {MC} + \frac{1}{2}\overrightarrow {CA} \\= \frac{3}{2}\overrightarrow {BC} + \frac{1}{2}\left( {\overrightarrow {BA} - \overrightarrow {BC} } \right)\\ = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \end{array}$ $\begin{array}{l}\overrightarrow {MP} = \overrightarrow {MC} + \overrightarrow {CP} = \overrightarrow {MC} + \frac{1}{2}\overrightarrow {CA} \\= \frac{3}{2}\overrightarrow {BC} + \frac{1}{2}\left( {\overrightarrow {BA} - \overrightarrow {BC} } \right)\\ = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA} \end{array}$

c) Ta có:

$\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} ; \overrightarrow {MP} = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA}$ $\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} + \frac{1}{4}\overrightarrow {BA} ; \overrightarrow {MP} = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {BA}$

$\Rightarrow \overrightarrow {MP} = 2\overrightarrow {MN}$ $\Rightarrow \overrightarrow {MP} = 2\overrightarrow {MN}$

Vậy M,N,P thẳng hàng

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 3: Tích của một số với một vectơ CTST. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán 10 CTST. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 CTST...

Chia sẻ, đánh giá bài viết

1

243

Bài trước

Bài sau