Giải Toán 10 Chân trời sáng tạo bài 1

Giải Toán 10 Bài 1: Mệnh đề CTST vừa được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để giải bài tập Toán 10 Chân trời sáng tạo. Mời các bạn cùng tham khỏa chi tiết bài viết dưới đây.

Giải bài 1 trang 14 SGK Toán 10 Chân trời Tập 1

Trong các khẳng định sau, khẳng định nào là mệnh đề, khẳng định nào là mệnh đề chứa biến

a) 3 + 2 > 5

b) 1 − 2x = 0

c) x − y = 2

d) 1 − \(\sqrt{2}\) < 0

Lời giải

Các khẳng định là mệnh đề là:

a) 3 + 2 > 5

d) 1 − \(\sqrt{2}\) < 0

Các khẳng định là mệnh đề chứa biến là:

b) 1 − 2x = 0

c) x − y = 2

Giải bài 2 trang 14 SGK Toán 10 Chân trời Tập 1

Xét tính đúng sai của các mệnh đề sau và phát biểu mệnh đề phủ định của chúng.

a) 2020 chia hết cho 3

b) π < 3,15

c) Nước ta hiện nay có 5 thành phố trực thuộc trung ương.

d) Tam giác có hai góc bằng 45^o là tam giác vuông cân.

Lời giải

a) Mệnh đề “2020 chia hết cho 3” sai.

Mệnh đề phủ định của mệnh đề này là: “2020 không chia hết cho 3”

b) Mệnh đề “π < 3,15” đúng vì π ≈ 3,141592654

Mệnh đề phủ định của mệnh đề này là: “π ≥ 3,15”

c) Mệnh đề “Nước ta hiện nay có 5 thành phố trực thuộc trung ương” đúng (gồm Hà Nội, Đà Nẵng, Hải Phòng, Hồ Chí Minh và Cần Thơ)

Mệnh đề phủ định của mệnh đề này là: “Nước ta hiện nay không phải có 5 thành phố trực thuộc trung ương”

d) Mệnh đề “Tam giác có hai góc bằng 45^o là tam giác vuông cân” đúng.

Mệnh đề phủ định của mệnh đề này là: “Tam giác có hai góc bằng 45^o không phải là tam giác vuông cân”

Giải bài 3 trang 14 SGK Toán 10 Chân trời Tập 1

Xét hai mệnh đề:

P: “Tứ giác ABCD là hình bình hành”.

Q: “Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường”.

a) Phát biểu mệnh đề P ⇒ Q và xét tính đúng sai của nó.

b) Phát biểu mệnh đề đảo của mệnh đề P ⇒ Q.

Lời giải

a) Mệnh đề P ⇒ Q: “Nếu tứ giác ABCD là hình bình hành thì nó có hai đường chéo cắt nhau tại trung điểm của mỗi đường”.

Mệnh đề này đúng vì “hai đường chéo cắt nhau tại trung điểm của mỗi đường” là tính chất của hình hình hành.

b) Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P, được phát biểu là: “Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm của mỗi đường thì nó là hình bình hành”.

Giải bài 4 trang 15 SGK Toán 10 Chân trời Tập 1

Cho các định lí:

P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”.

Q: “Nếu a<b thì a+c<b+c” (a, b, c ∈ R).

a) Chỉ ra giả thiết và kết luận của mỗi định lí.

b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”.

c) Mệnh đề đảo của mỗi định lí đó có là định lí không?

Lời giải

a) Chỉ ra giả thiết và kết luận của mỗi định lí;

Xét định lý P: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau” có:

Giả thiết: Nếu hai tam giác bằng nhau.

Kết luận: Diện tích của chúng bằng nhau.

Xét định lý Q: “Nếu a < b thì a + c < b + c” (a, b, c ∈ ℝ), có:

Giả thiết: a < b

Kết luận: a + c < b + c

b) Phát biểu lại mỗi định lí đã cho, sử dụng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”:

Bằng thuật ngữ “điều kiện cần” hoặc “điều kiện đủ”, các định lý đã cho được phát biểu như sau:

Định lý P:

Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau.

Hai tam giác có diện tích bằng nhau là điều kiện cần để hai tam giác bằng nhau.

Định lý Q:

a < b là điều kiện đủ để có a + c < b + c.

a + c < b + c là điều kiện cần để có a < b.

c) +) Mệnh đề đảo của định lí P là: “Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau”.

Mệnh đề này là mệnh đề sai, chẳng hạn hai tam giác sau ABC và MNP có cùng diện tích là 7,5 (đvdt) nhưng hai tam giác này không bằng nhau.

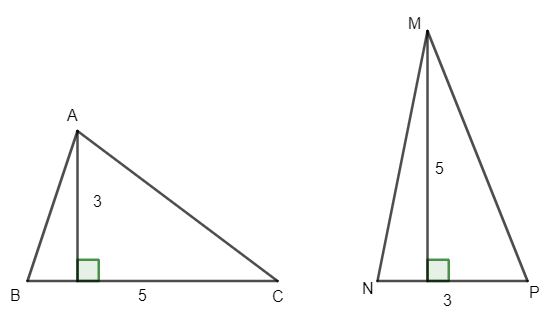
Do đó mệnh đề đảo của định lí P không là định lí.

+) Mệnh đề đảo của định lí Q là: “Nếu a + c < b + c thì a < b”.

Mệnh đề này là một mệnh đề đúng, vì:

Ta có: a + c < b + c

⇔ a + c + (-c) < b + c + (-c) (liên hệ giữa thứ tự và phép cộng)

⇔ a < b.

Do đó mệnh đề đảo của định lí Q là một định lí.

Giải bài 5 trang 15 SGK Toán 10 Chân trời Tập 1

Sử dụng thuật ngữ “điều kiện cần và đủ”, phát biểu các định lí sau:

a) Một phương trình bậc hai có hai nghiệm phân biệt khi và chỉ khi biệt thức của nó dương;

b) Một hình bình hành là hình thoi thì nó có hai đường chéo vuông góc với nhau và ngược lại.

Lời giải

Sử dụng thuật ngữ “điều kiện cần và đủ”, các định lí được phát biểu như sau:

a) Một phương trình bậc hai có hai nghiệm phân biệt là điều kiện cần và đủ để biệt thức của nó dương.

b) Một hình bình hành là hinh thoi là điều kiện cần và đủ để hai đường chéo vuông góc với nhau.

Giải bài 6 trang 15 SGK Toán 10 Chân trời Tập 1

Cho các mệnh đề sau:

P: “Giá trị tuyệt đối của mọi số thực đều lớn hơn hoặc bằng chính nó”;

Q: “Có số tự nhiên sao cho bình phương của nó bằng 10”;

R: “Có số thực x sao cho x² + 2x – 1 = 0”.

a) Xét tính đúng sai của mỗi mệnh đề trên.

b) Sử dụng kí hiệu ∀, ∃ để viết lại các mệnh đề đã cho.

Lời giải

a) Mệnh đề P đúng, vì: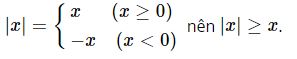

Mệnh đề Q sai vì chỉ có các số ±\(\sqrt{10}\) có bình phương bằng 10, nhưng \(\sqrt{10}\) và −\(\sqrt{10}\) đều không là số tự nhiên.

Mệnh đề R đúng vì x = −1 + \(\sqrt{2}\) ∈ R thỏa mãn x² + 2x − 1 = 0.

b) Có thể viết lại các mệnh đề trên như sau:

P: “∀ x ∈ R, |x| ≥ x”

Q: “∃ n ∈ N, n² = 10”

R: “∃ x ∈ R, x² + 2x − 1 = 0”

Giải bài 7 trang 15 SGK Toán 10 Chân trời Tập 1

Xét tính đúng sai và viết mệnh đề phủ định của các mệnh đề sau đây:

a) ∃ x ∈ N, x + 3 = 0

b) ∀ x ∈ R, x² + 1 ≥ 2x

c) ∀ a ∈ R, \(\sqrt{a^{2}}\) = a

Lời giải

a) Mệnh đề sai, vì chỉ có x = −3 thảo mãn x + 3 = 0 nhưng −3 ∉ N.

Mệnh đề phủ định của mệnh đề này là: “∀ x ∈ N, x + 3 ≠ 0”.

b) Mệnh đề đúng, vì (x − 1)² ≥ 0 hay x² + 1 ≥ 2x với mọi số thực x.

Mệnh đề phủ định của mệnh đề này là: “∃ x ∈ R, x² + 1 < 2x”

c) Mệnh đề sai, vì có a = −2 ∈ R, \(\sqrt{\left(-2\right)^2}\) = 2 ≠ a

Mệnh đề phủ định của mệnh đề này là: “∃ a ∈ R, \(\sqrt{a^2}\) ≠ a”.

----------------------------

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 1: Mệnh đề CTST. Bài viết hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 CTST Tập 1. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 10 nhé. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 CTST, Tiếng Anh lớp 10...

• Giải Toán 10 Bài 2: Tập hợp CTST