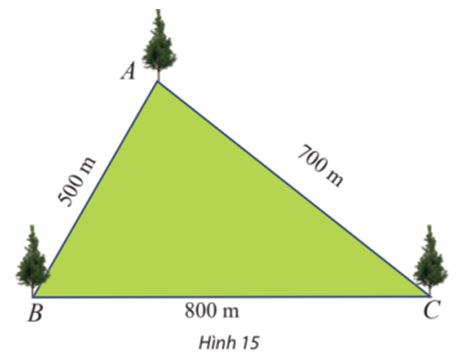
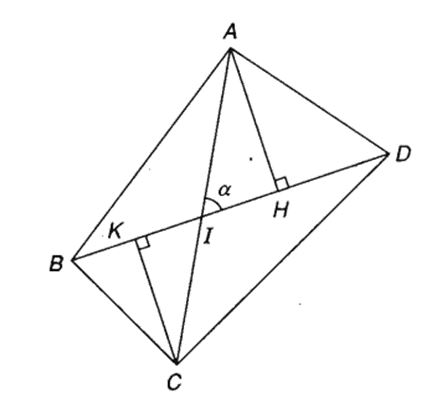
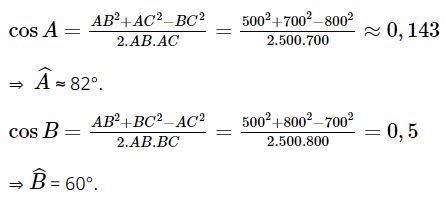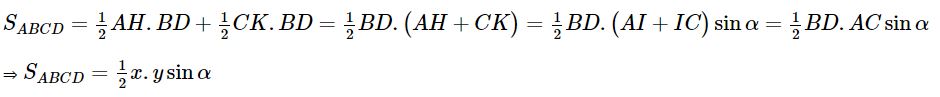![]() \(S\;=\;\frac12\;.\;AC\;.\;AB\;.\;\sin A\;=\;\frac12\;.\;6\;.\;8\;.\;\sin60^o\;=\;\frac12\;.\;6\;.\;8\;.\;\frac{\sqrt3}2\;=\;12\sqrt3\;\approx\;20,8\)
\(S\;=\;\frac12\;.\;AC\;.\;AB\;.\;\sin A\;=\;\frac12\;.\;6\;.\;8\;.\;\sin60^o\;=\;\frac12\;.\;6\;.\;8\;.\;\frac{\sqrt3}2\;=\;12\sqrt3\;\approx\;20,8\)
Vậy diện tích tam giác ABC là 20,8 (đơn vị diện tích).
b) Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA = 62 + 82 – 2.6.8.cos60° = 52
⇒ BC =  \(\sqrt{52}\) ≈ 7,2.
\(\sqrt{52}\) ≈ 7,2.
Mặt khác diện tích tam giác ABC:
![]() \(S\;=\;\frac{AB\;.\;AC\;.\;BC}{4R}\;\Rightarrow\;R\;=\;\frac{AB\;.\;AC\;.\;BC}{4S}\;=\;\frac{6\;.\;8\;.\;\sqrt{52}}{4\;.\;12\sqrt3}\;\approx\;4\;,\;2\)
\(S\;=\;\frac{AB\;.\;AC\;.\;BC}{4R}\;\Rightarrow\;R\;=\;\frac{AB\;.\;AC\;.\;BC}{4S}\;=\;\frac{6\;.\;8\;.\;\sqrt{52}}{4\;.\;12\sqrt3}\;\approx\;4\;,\;2\)
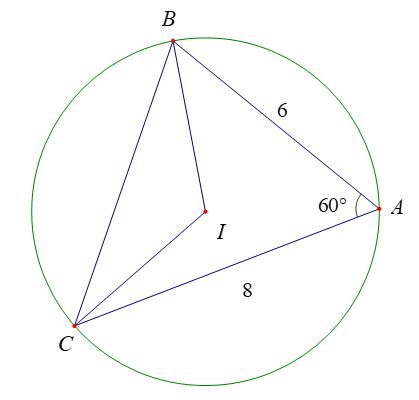
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên ta có IA = IB = IC = R = 4,2.
Nửa chu vi của tam giác IBC: ![]() \(p\;=\;\frac{IB\;+\;IC\;+\;BC}2\;=\;\frac{4,2\;+\;4,2\;+\;7,2}2\;=\;7,8\\\)
\(p\;=\;\frac{IB\;+\;IC\;+\;BC}2\;=\;\frac{4,2\;+\;4,2\;+\;7,2}2\;=\;7,8\\\)
Áp dụng công thức Heron ta tính được diện tích tam giác IBC:
![]() \(S\;=\;\sqrt{7,8\;.\;(7,8\;-\;4,2)\;.\;(7,8\;-\;4,2)\;.\;(7,8\;-\;7,2)}\;\approx\;\sqrt{60,7}\;\approx\;7,8\)
\(S\;=\;\sqrt{7,8\;.\;(7,8\;-\;4,2)\;.\;(7,8\;-\;4,2)\;.\;(7,8\;-\;7,2)}\;\approx\;\sqrt{60,7}\;\approx\;7,8\)
Vậy diện tích tam giác IBC là 7,8 (đơn vị diện tích).
a) Áp dụng công thức tính diện tích tam giác ta có:
![]() \(S\;=\;\frac12\;\;AC\;.\;AB\;.\;\sin A\;=\;\frac12\;.\;6\;.\;8\;.\;\sin\;60^o\;=\;\frac12\;.\;6\;.\;8\;.\;\frac{\sqrt3}2\;=\;12\sqrt3\;\approx\;20\;,\;8\)
\(S\;=\;\frac12\;\;AC\;.\;AB\;.\;\sin A\;=\;\frac12\;.\;6\;.\;8\;.\;\sin\;60^o\;=\;\frac12\;.\;6\;.\;8\;.\;\frac{\sqrt3}2\;=\;12\sqrt3\;\approx\;20\;,\;8\)
Vậy diện tích tam giác ABC là 20,8 (đơn vị diện tích).
b) Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA = 62 + 82 – 2.6.8.cos60° = 52
⇒ BC = ![]() \(\sqrt{52}\) ≈ 7,2.
\(\sqrt{52}\) ≈ 7,2.
Mặt khác diện tích tam giác ABC:
![]() \(S\;=\;\frac{AB\;.\;AC\;.\;BC}{4R}\;\Rightarrow\;R\;=\;\frac{AB\;.\;AC\;.\;BC}{4S}\;=\;\frac{6\;.\;8\;.\;\sqrt{52}}{4\;.\;12\sqrt3}\;\approx\;4,2\)
\(S\;=\;\frac{AB\;.\;AC\;.\;BC}{4R}\;\Rightarrow\;R\;=\;\frac{AB\;.\;AC\;.\;BC}{4S}\;=\;\frac{6\;.\;8\;.\;\sqrt{52}}{4\;.\;12\sqrt3}\;\approx\;4,2\)
Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên ta có IA = IB = IC = R = 4,2.
Nửa chu vi của tam giác IBC: ![]() \(p\;=\;\frac{IB\;+\;IC\;+\;BC}2\;=\;\frac{4,2\;+\;4,2\;+\;7,2}2\;=\;7\;,\;8\)
\(p\;=\;\frac{IB\;+\;IC\;+\;BC}2\;=\;\frac{4,2\;+\;4,2\;+\;7,2}2\;=\;7\;,\;8\)
Áp dụng công thức Heron ta tính được diện tích tam giác IBC:
![]() \(S\;=\;\sqrt{7,8\;.\;(7,8\;-\;4,2)\;.\;(7,8\;-\;4,2)\;.\;(7,8\;-\;7,2)}\;\approx\;\sqrt{60,7}\;\approx\;7,8\)
\(S\;=\;\sqrt{7,8\;.\;(7,8\;-\;4,2)\;.\;(7,8\;-\;4,2)\;.\;(7,8\;-\;7,2)}\;\approx\;\sqrt{60,7}\;\approx\;7,8\)
Vậy diện tích tam giác IBC là 7,8 (đơn vị diện tích).