Giải Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn CTST
Giải Toán 10 CTST Bài 1: Bất phương trình bậc nhất hai ẩn
Giải Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn CTST vừa được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 10. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.
Bài 1 trang 32 SGK Toán 10 CTST Tập 1
Cho bất phương trình bậc nhất hai ẩn x - 2y + 6 > 0.
a) (0 ; 0) có phải là một nghiệm của bất phương trình đã cho không?
b) Chỉ ra ba cặp số (x ; y) là nghiệm của bất phương trình đã cho.
c) Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng tọa độ Oxy.
Lời giải
a) Với cặp (0 ; 0) ta có : 0 – 2.0 + 6 = 6 > 0 nên (0 ; 0) là nghiệm của bất phương trình đã cho.
Vậy (0 ; 0) là một nghiệm của bất phương trình x - 2y + 6 > 0.
b)
+ Lấy cặp số (1 ; 0) ta có 1 – 2.0 + 6 = 7 > 0 nên cặp số (1 ; 0) là một nghiệm của bất phương trình x - 2y + 6 > 0.
+ Lấy cặp số (0 ; 1) ta có 0 – 2.1 + 6 = 4 > 0 nên cặp số (0 ; 1) là một nghiệm của bất phương trình x - 2y + 6 > 0.
+ Lấy cặp số (-1 ; -1) ta có –1 – 2. (–1) + 6 = 7 > 0 nên cặp số (-1 ; -1) là một nghiệm của bất phương trình x - 2y + 6 > 0.
Vậy ta có ba cặp số (1 ; 0) ; (0 ; 1) ; (-1 ; -1) đều là nghiệm của bất phương trình x - 2y + 6 > 0.
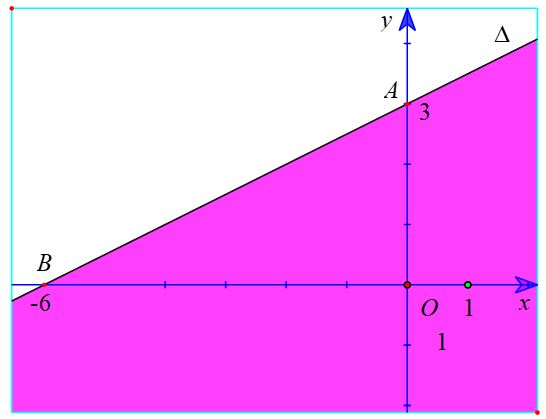
c) Vẽ đường thẳng ∆ : x – 2y + 6 = 0 đi qua hai điểm A(0; 3); B(-6; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và (0 ; 0) là một nghiệm của bất phương trình
x - 2y + 6 > 0.
Do đó, miền nghiệm của bất phương trình x - 2y + 6 > 0 là nửa mặt phẳng không kể bờ ∆, chứa điểm O (là miền được tô màu trong hình sau).
Bài 2 trang 32 SGK Toán 10 CTST Tập 1
Biểu diễn tập nghiệm của các bất phương trình sau trên mặt phẳng tọa độ Oxy.
a) – x + y + 2 > 0
b) y + 2 ≥ 0
c ) – x + 2 ≤ 0.
Lời giải
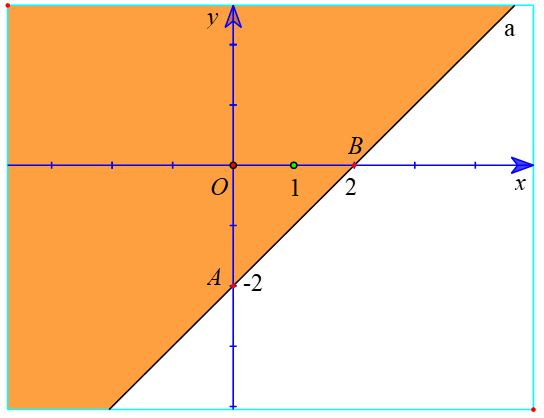
a) Vẽ đường thẳng a: – x + y + 2 = 0 đi qua hai điểm A (0; - 2); B (2; 0).
Xét gốc tọa độ O (0 ; 0). Ta thấy O ∉ a và – 0 + 0 + 2 = 2 > 0.
Suy ra (0 ; 0) là một nghiệm của bất phương trình – x + y + 2 > 0.
Do đó, miền nghiệm của bất phương trình – x + y + 2 > 0 là nửa mặt phẳng không kể bờ a, chứa điểm O (là miền tô màu trong hình sau).
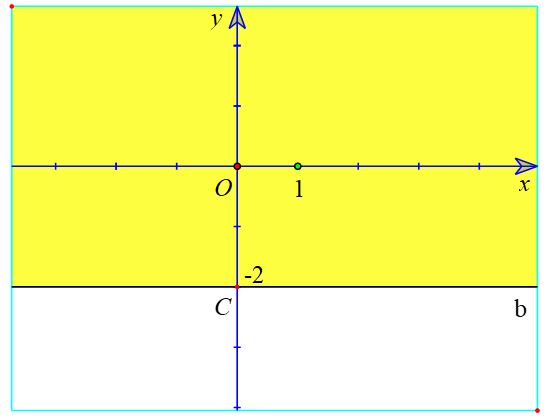
b) Vẽ đường thẳng b: y + 2 = 0 đi qua điểm C (0; -2) và song song với trục Ox
Xét gốc tọa độ O (0 ; 0). Ta thấy O ∉ b và 0 + 2 = 2 > 0
Suy ra (0 ; 0) là nghiệm của bất phương trình y + 2 ≥ 0.
Do đó, miền nghiệm của bất phương trình y + 2 ≥ 0 là nửa mặt phẳng kể cả bờ b, chứa điểm O (là miền tô màu vàng trong hình sau).
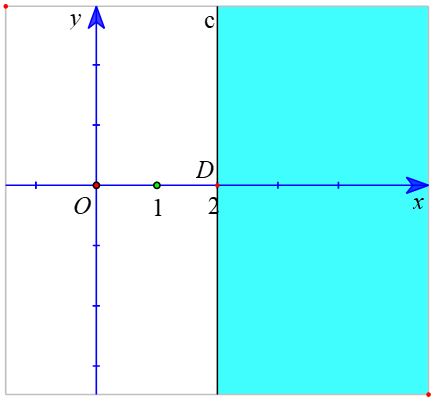
c) ) Vẽ đường thẳng c : – x + 2 = 0.đi qua điểm D (2; 0) và song song với trục Oy.
Xét gốc tọa độ O (0 ; 0). Ta thấy O ∉ c và – 0 + 2 = 2 > 0
Suy ra (0 ; 0) không là nghiệm của bất phương trình – x + 2 ≤ 0.
Do đó, miền nghiệm của bất phương trình – x + 2 ≤ 0.là nửa mặt phẳng kể cả bờ c, không chứa điểm O (là miền tô màu xanh trong hình sau).
Bài 3 trang 32 SGK Toán 10 CTST Tập 1
Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ oxy
a) – x + 2 + 2 (y – 2) < 2 (1 – x)
b) 3(x – 1 ) + 4(y – 2) < 5x – 3.
Lời giải
a) Ta có: – x + 2 + 2(y – 2 ) < 2(1 – x)
⇔ – x + 2 + 2(y – 2 ) – 2(1 – x) < 0
⇔ – x + 2 + 2y – 4 – 2 + 2x < 0
⇔ x + 2y – 4 < 0
Ta sẽ biểu diễn miền nghiệm của bất phương trình x + 2y – 4 < 0.
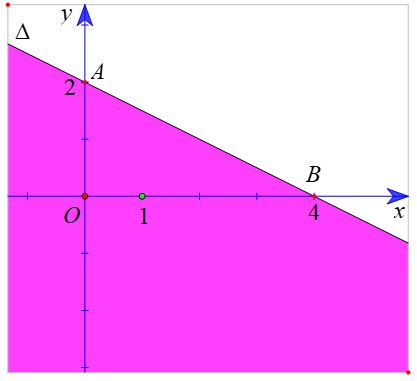
Vẽ đường thẳng ∆: x + 2y – 4 = 0 đi qua điểm A (0; 2) và B (4 ; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và 0 + 2.0 – 4 = – 4 < 0.
Suy ra (0 ; 0) là nghiệm của bất phương trình x + 2y – 4 < 0.
Do đó, miền nghiệm của bất phương trình x + 2y – 4 < 0 là nửa mặt phẳng không kể bờ ∆, chứa điểm O (là miền tô màu trong hình sau).
b) Ta có: 3(x – 1 ) + 4(y – 2) < 5x – 3
⇔ 3x – 3 + 4y – 8 – 5x + 3 < 0
⇔ – 2x + 4y – 8 < 0
⇔ – x + 2y – 4 < 0
Ta sẽ biểu diễn miền nghiệm của bất phương trình – x + 2y – 4 < 0
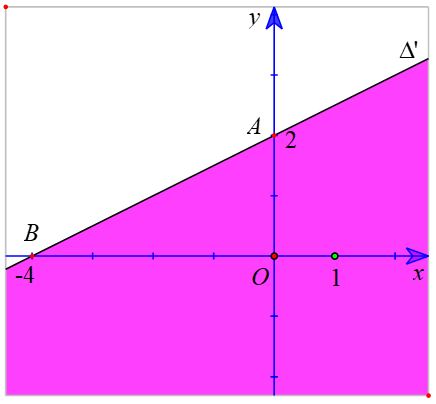
Vẽ đường thẳng ∆’ : – x + 2y – 4 = 0 đi qua điểm A(0; 2) và B (– 4 ; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆’ và – 0 + 2. 0 – 4 = – 4 < 0.
Suy ra (0 ; 0) là nghiệm của bất phương trình – x + 2y – 4 < 0.
Do đó, miền nghiệm của bất phương trình –x + 2y – 4 < 0 là nửa mặt phẳng không kể bờ ∆’, chứa điểm O (là miền tô màu trong hình sau).
Bài 4 trang 32 SGK Toán 10 CTST Tập 1
Bạn Cúc muốn pha hai loại nước cam. Để pha một lít nước cam loại I cần 30 g bột cam, còn một lít nước cam loại II cần 20 g bột cam. Gọi x và y lần lượt là số lít nước cam loại I và II pha chế được. Biết rằng Cúc chỉ có thể dùng không quá 100 g bột cam. Hãy lập các bất phương trình mô tả số lít nước cam loại I và II mà bạn Cúc có thể pha chế được và biểu diễn miền nghiệm của các bất phương trình đó trên cùng một mặt phẳng tọa độ Oxy.
Lời giải
Vì x, y là là số lít nước cam loại I và II pha chế được nên x ≥ 0 và y ≥ 0.
Số gam bột cam cần dùng để pha chế x lít nước cam loại I là: 30x (g).
Số gam bột cam cần dùng để pha chế y lít nước cam loại II là: 20y (g).
Số gam bột cam Cúc cần dùng để pha hai loại nước cam là : 30x + 20y (g).
Vì số bột cam Cúc có thể dùng không quá 100 g nên ta có bất phương trình : 30x + 20y ≤ 100 hay 3x + 2y ≤ 10.
Vậy ta có ba bất phương trình mô tả số lít nước cam loại I và II mà bạn Cúc có thể pha chế được là:
x ≥ 0;
y ≥ 0;
3x + 2y – 10 ≤ 0.
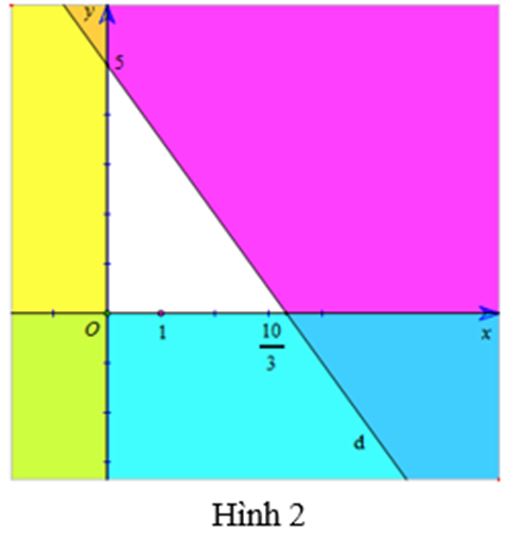
Biểu diễn miền nghiệm của ba bất phương trình trên cùng một mặt phẳng tọa độ Oxy ta được:
+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bên phải trục Ox, kể cả bờ Ox, (là miền không tô màu vàng trong hình 2).
+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía trên trục Oy, kể cả bờ Oy, (là miền không tô màu xanh trong hình 2).
+ Miền nghiệm của bất phương trình 3x + 2y – 10 ≤ 0 là nửa mặt phẳng kể cả bờ d, chứa điểm O (là miền không tô màu tím trong hình 2).
Bài 5 trang 32 SGK Toán 10 CTST Tập 1
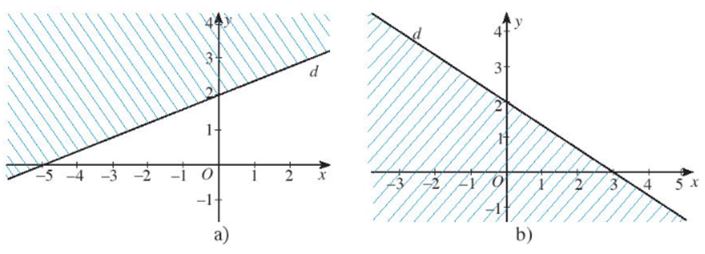
Miền không gạch chéo (không kể bờ d) trong mỗi hình dưới đây là miền nghiệm của bất phương trình nào?
Lời giải
a) Giả sử phương trình đường thẳng d có dạng là y = ax + b
Đường thẳng d đi qua hai điểm (0; 2) và (- 5; 0) nên ta có:
\(\left\{\begin{array}{l}2=a.0+b\\0=a.(-5)+b\end{array}\right.\)
Giải hệ trên ta được a = \(\frac25\), b = 2. Suy ra y = \(\frac25\)x + 2 hay 2x – 5y + 10 = 0.
Vậy ta có phương trình đường thẳng d là 2x – 5y + 10 = 0.
Mặt khác O (0; 0) không thuộc d và thuộc miền nghiệm của bất phương trình.
Mà 2.0 – 5.0 + 10 = 10 > 0.
Hơn nữa miền nghiệm không kể đường thẳng d nên bất phương trình cần tìm là 2x – 5y + 10 > 0.
b) Giả sử phương trình đường thẳng d có dạng là y = ax + b
Đường thẳng d đi qua hai điểm (3; 0) và (0; 2) nên ta có:
\(\left\{\begin{array}{l}0=a.3+b\\2=a.0+b\end{array}\right.\)
Giải hệ trên ta được a = −\(\frac23\) , b = 2. Suy ra y = −\(\frac23\)x + 2 hay 2x + 3y – 6 = 0.
Vậy ta có phương trình đường thẳng d là 2x + 3y – 6 = 0.
Mặt khác O (0; 0) không thuộc d và không thuộc miền nghiệm của bất phương trình.
Mà 2.0 + 3.0 – 6 = – 6 < 0.
Hơn nữa miền nghiệm của bất phương trình không kể đường thẳng d nên bất phương trình cần tìm là 2x + 3y – 6 > 0.
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn CTST. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài viết rồi đúng không ạ? Bài viết đã hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 CTST. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 CTST, Tiếng Anh lớp 10...
