VnDoc.com

Giải Toán 10 Bài tập cuối chương 9 CTST

Toán 10 Chân trời sáng tạo Tập 2

Bài trước

Bài sau

Bài tập cuối chương 9 CTST

Bài 1 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2
Bài 2 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2
Bài 3 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2
Bài 4 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2
Bài 5 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2
Bài 6 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2
Bài 7 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2
Bài 8 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2
Bài 9 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Giải Toán 10 Bài tập cuối chương 9 CTST được VnDoc.com sưu tầm và xin gửi tới bạn đọc. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

Bài 1 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2).

a. Chứng minh ABCD là hình vuông.

b. Tìm tọa độ tâm I của hình vuông ABCD.

Gợi ý đáp án

a. Ta có: $\vec{AB} = (-1; 3), \vec{DC} = (-1; 3) \Rightarrow \vec{AB} = \vec{DC}$ $\vec{AB} = (-1; 3), \vec{DC} = (-1; 3) \Rightarrow \vec{AB} = \vec{DC}$

$\Rightarrow$ $\Rightarrow$ ABCD là hình bình hành.

Lại có: $\vec{AD} = (3; 1) \Rightarrow \vec{AB}. \vec{AD} = -1. 3 + 3. 1 = 0$ $\vec{AD} = (3; 1) \Rightarrow \vec{AB}. \vec{AD} = -1. 3 + 3. 1 = 0$

$\Rightarrow \vec{AB} \perp \vec{AD} hay AB \perp AD$ $\Rightarrow \vec{AB} \perp \vec{AD} hay AB \perp AD$

$\Rightarrow$ $\Rightarrow$ Hình bình hành ABCD là hình chữ nhật.

Ta có: $AD = |\vec{AD}| = \sqrt{3^{2} + 1^{2}} = \sqrt{10}$ $AD = |\vec{AD}| = \sqrt{3^{2} + 1^{2}} = \sqrt{10}$

$AB = |\vec{AB}| = \sqrt{(-1)^{2} + 3^{2}} = \sqrt{10}$ $AB = |\vec{AB}| = \sqrt{(-1)^{2} + 3^{2}} = \sqrt{10}$

$\Rightarrow AB = AD \Rightarrow$ $\Rightarrow AB = AD \Rightarrow$ Hình chữ nhật ABCD là hình vuông (đpcm).

b. Tâm I của hình vuông ABCD là trung điểm của $AC \Rightarrow I = (\frac{2 + 4}{2}; \frac{1+5}{2}) \Leftrightarrow I = (3; 3)$ $AC \Rightarrow I = (\frac{2 + 4}{2}; \frac{1+5}{2}) \Leftrightarrow I = (3; 3)$

Vậy I = (3; 3).

Bài 2 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Cho AB và CD là dây cung vuông góc tại E của đường tròn (O). Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ để chứng minh EF vuông góc với DB.

Gợi ý đáp án

Chọn hệ tọa độ Oxy như hình vẽ. A(a; 0), B(b; 0), C(0; c), D(0; d). Hai dây cung AB và CD vuông góc với nhau tại E (trùng với gốc tọa độ O).

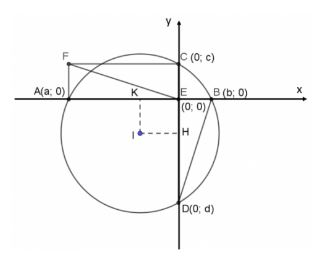
Giải Toán 10 Bài tập cuối chương 9 CTST

Vì ACEF là hình chữ nhật nên F(a; c).

Gọi I là tâm đường tròn (O), K và H lần lượt là chân đường cao hạ từ I tới AB, CD.

$\Rightarrow K$ $\Rightarrow K$ là trung điểm của $AB \Rightarrow K = (\frac{a + b}{2}; 0)$ $AB \Rightarrow K = (\frac{a + b}{2}; 0)$

H là trung điểm của $CD \Rightarrow H = (0; \frac{c + d}{2})$ $CD \Rightarrow H = (0; \frac{c + d}{2})$

$\Rightarrow I = (\frac{a + b}{2}; \frac{c + d}{2})$ $\Rightarrow I = (\frac{a + b}{2}; \frac{c + d}{2})$

Ta có: $\vec{IA} = (a - \frac{a + b}{2}; -\frac{c + d}{2}) = (\frac{a - b}{2}; -\frac{c + d}{2})$ $\vec{IA} = (a - \frac{a + b}{2}; -\frac{c + d}{2}) = (\frac{a - b}{2}; -\frac{c + d}{2})$

$\vec{IC} = ( -\frac{a + b}{2}; c - \frac{c + d}{2}) = (-\frac{a + b}{2}; \frac{c - d}{2}$ $\vec{IC} = ( -\frac{a + b}{2}; c - \frac{c + d}{2}) = (-\frac{a + b}{2}; \frac{c - d}{2}$

Vì $IA = IC (=R) \Rightarrow (\frac{a - b}{2})^{2} + (-\frac{c + d}{2})^{2} = (-\frac{a + b}{2})^{2} + (\frac{c - d}{2})^{2}$ $IA = IC (=R) \Rightarrow (\frac{a - b}{2})^{2} + (-\frac{c + d}{2})^{2} = (-\frac{a + b}{2})^{2} + (\frac{c - d}{2})^{2}$

$\Leftrightarrow (a - b)^{2} + (c + d)^{2} = (a + b)^{2} + (c - d)^{2}$ $\Leftrightarrow (a - b)^{2} + (c + d)^{2} = (a + b)^{2} + (c - d)^{2}$

$\Leftrightarrow a^{2} - 2ab + b^{2} + c^{2} + 2cd + d^{2} = a^{2} + 2ab + b^{2} + c^{2} - 2cd + d^{2}$ $\Leftrightarrow a^{2} - 2ab + b^{2} + c^{2} + 2cd + d^{2} = a^{2} + 2ab + b^{2} + c^{2} - 2cd + d^{2}$

$\Leftrightarrow 4ab = 4cd \Leftrightarrow ab = cd \Leftrightarrow ab - cd = 0$ $\Leftrightarrow 4ab = 4cd \Leftrightarrow ab = cd \Leftrightarrow ab - cd = 0$

$\Rightarrow \vec{EF}. \vec{BD} = (-a).(-b) - c.d = ab - cd = 0$ $\Rightarrow \vec{EF}. \vec{BD} = (-a).(-b) - c.d = ab - cd = 0$ (chứng minh trên)

$\Rightarrow \vec{EF} \perp \vec{BD} hay EF \perp BD (đpcm).$ $\Rightarrow \vec{EF} \perp \vec{BD} hay EF \perp BD (đpcm).$

Bài 3 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Tìm tọa độ giao điểm và góc giữa hai đường thẳng $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ trong mỗi trường hợp sau:

a. $d_{1}: x - y + 2 = 0$ $d_{1}: x - y + 2 = 0$ và $d_{2}: x + y + 4 = 0;$ $d_{2}: x + y + 4 = 0;$

b. $d_{1}: \left\{\begin{matrix}x = 1 + t\\y = 3 + 2t \end{matrix}\right.$ $d_{1}: \left\{\begin{matrix}x = 1 + t\\y = 3 + 2t \end{matrix}\right.$ và $d_{2}: x - 3y + 2 = 0;$ $d_{2}: x - 3y + 2 = 0;$

c. $d_{1}: \left\{\begin{matrix}x = 2 - t\\y = 5 + 3t \end{matrix}\right. và d_{2}: \left\{\begin{matrix}x = 1 + 3t$ $d_{1}: \left\{\begin{matrix}x = 2 - t\\y = 5 + 3t \end{matrix}\right. và d_{2}: \left\{\begin{matrix}x = 1 + 3t'\\3 + 1t' \end{matrix}\right.$

Gợi ý đáp án

a. Đường thẳng $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ có vectơ pháp tuyến lần lượt là $\vec{n_{1}} = (1; -1) và \vec{n_{2}} = (1; 1).$ $\vec{n_{1}} = (1; -1) và \vec{n_{2}} = (1; 1).$

Ta có: $\vec{n_{1}}. \vec{n_{2}} = 1. 1 + (-1). 1 = 0 nên \vec{n_{1}} và \vec{n_{2}}$ $\vec{n_{1}}. \vec{n_{2}} = 1. 1 + (-1). 1 = 0 nên \vec{n_{1}} và \vec{n_{2}}$ là hai vectơ vuông góc $\Rightarrow d_{1} \perp d_{2} \Rightarrow (d_{1}, d_{2}) = 90^{\circ}.$ $\Rightarrow d_{1} \perp d_{2} \Rightarrow (d_{1}, d_{2}) = 90^{\circ}.$

Giao điểm M của $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}x - y + 2 = 0\\x + y + 4 = 0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = -3 \\y = -1\end{matrix}\right.$ $\left\{\begin{matrix}x - y + 2 = 0\\x + y + 4 = 0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = -3 \\y = -1\end{matrix}\right.$

Vậy $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$vuông góc và cắt nhau tại M(-3; -1).

b. Ta có: $\vec{u_{1}} = (1; 2)$ $\vec{u_{1}} = (1; 2)$ là vectơ chỉ phương của $d_{1} \Rightarrow \vec{n_{1}} = (2; -1)$ $d_{1} \Rightarrow \vec{n_{1}} = (2; -1)$ là vectơ pháp tuyến của $d_{1}.$ $d_{1}.$

Phương trình tổng quát của $d_1$ đi qua điểm A(1; 3) và nhận $\vec{n_{1}} = (2; -1)$ $\vec{n_{1}} = (2; -1)$ làm vectơ pháp tuyến là: $2(x - 1) - (y - 3) = 0 \Leftrightarrow 2x - y + 1 = 0$ $2(x - 1) - (y - 3) = 0 \Leftrightarrow 2x - y + 1 = 0$

Đường thẳng $d_{2}$ $d_{2}$ có vectơ pháp tuyến là $\vec{n_{2}} = (1; -3)$ $\vec{n_{2}} = (1; -3)$

Ta có: $\frac{2}{1} \neq \frac{-1}{-3} \Rightarrow \vec{n_{1}}$ $\frac{2}{1} \neq \frac{-1}{-3} \Rightarrow \vec{n_{1}}$ và $\vec{n_{2}}$ $\vec{n_{2}}$ là hai vectơ không cùng phương.

$\Rightarrow d_{1} và d_{2}$ $\Rightarrow d_{1} và d_{2}$ cắt nhau. Giao điểm M của $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}2x - y + 1 = 0\\x - 3y + 2 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{-1}{5}\\y = \frac{3}{5}\end{matrix}\right.$ $\left\{\begin{matrix}2x - y + 1 = 0\\x - 3y + 2 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{-1}{5}\\y = \frac{3}{5}\end{matrix}\right.$

Ta có: $cos(d_{1}, d_{2}) = \frac{|2. 1 + (-1). (-3)|}{\sqrt{2^{2} + (-1)^{2}}.\sqrt{1^{2} + (-3)^{2}}} = \frac{\sqrt{2}}{2} \Rightarrow (d_{1}, d_{2}) = 45^{\circ}$ $cos(d_{1}, d_{2}) = \frac{|2. 1 + (-1). (-3)|}{\sqrt{2^{2} + (-1)^{2}}.\sqrt{1^{2} + (-3)^{2}}} = \frac{\sqrt{2}}{2} \Rightarrow (d_{1}, d_{2}) = 45^{\circ}$

Vậy $d_{1}$ $d_{1}$ cắt $d_{2}$ $d_{2}$ tại điểm $M(\frac{-1}{5}; \frac{3}{5}) và (d_{1}, d_{2}) = 45^{\circ}.$ $M(\frac{-1}{5}; \frac{3}{5}) và (d_{1}, d_{2}) = 45^{\circ}.$

c. Phương trình tổng quát của $d_{1} và d_{2}$ $d_{1} và d_{2}$lần lượt là:

$d_{1}: 3x + y - 11 = 0 và d_{2}: x - 3y + 8 = 0$ $d_{1}: 3x + y - 11 = 0 và d_{2}: x - 3y + 8 = 0$

Ta có: $\vec{n_{1}}. \vec{n_{2}} = 3. 1 + 1. (-3) = 0 \Rightarrow \vec{n_{1}} \perp \vec{n_{2}} hay d_{1} \perp d_{2} \Rightarrow (d_{1}, d_{2}) = 90^{\circ}.$ $\vec{n_{1}}. \vec{n_{2}} = 3. 1 + 1. (-3) = 0 \Rightarrow \vec{n_{1}} \perp \vec{n_{2}} hay d_{1} \perp d_{2} \Rightarrow (d_{1}, d_{2}) = 90^{\circ}.$

Giao điểm M của đường thẳng $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}3x + y - 11 = 0\\x - 3y + 8 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{5}{2}\\y = \frac{7}{2}\end{matrix}\right.$ $\left\{\begin{matrix}3x + y - 11 = 0\\x - 3y + 8 = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x = \frac{5}{2}\\y = \frac{7}{2}\end{matrix}\right.$

Vậy $d_{1}$ $d_{1}$ và $d_{2}$ $d_{2}$vuông góc và cắt nhau tại $M(\frac{5}{2}; \frac{7}{2}).$ $M(\frac{5}{2}; \frac{7}{2}).$

Bài 4 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Tính bán kính của đường tròn tâm M(-2; 3) và tiếp xúc với đường thẳng:

Gợi ý đáp án

d: 14x - 5y + 60 = 0

Ta có: $R = d(M; d) = \frac{|14. (-2) - 5. 3 + 60|}{\sqrt{14^{2} + (-5)^{2}}} = \frac{\sqrt{221}}{13}$ $R = d(M; d) = \frac{|14. (-2) - 5. 3 + 60|}{\sqrt{14^{2} + (-5)^{2}}} = \frac{\sqrt{221}}{13}$

Bài 5 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Tính khoảng cách giữa hai đường thẳng:

$\Delta$ $\Delta': 3x + 4y - 27 = 0$

Gợi ý đáp án

Ta có: $\frac{6}{3} = \frac{8}{4} \neq \frac{-13}{-27} \Rightarrow \Delta // \Delta$ $\frac{6}{3} = \frac{8}{4} \neq \frac{-13}{-27} \Rightarrow \Delta // \Delta'$

Lấy điểm $A(0; \frac{13}{8}) \in \Delta.$ $A(0; \frac{13}{8}) \in \Delta.$

Ta có: $d(\Delta, \Delta$ $d(\Delta, \Delta') = d(A; \Delta') = \frac{|4.\frac{13}{8}-27|}{\sqrt{3^{2} + 4^{2}}} = \frac{41}{10}$

Bài 6 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Tìm tâm và bán kính của các đường tròn có phương trình:

$a. (x - 2)^{2} + (y - 7)^{2} = 64;$ $a. (x - 2)^{2} + (y - 7)^{2} = 64;$

$b. (x + 3)^{2} + (y + 2)^{2} = 8;$ $b. (x + 3)^{2} + (y + 2)^{2} = 8;$

$c. x^{2} + y^{2} - 4x - 6y - 12 = 0.$ $c. x^{2} + y^{2} - 4x - 6y - 12 = 0.$

Gợi ý đáp án

a. Phương trình đường tròn có dạng $(x - a)^{2} + (y - b)^{2} = R^{2}$ $(x - a)^{2} + (y - b)^{2} = R^{2}$

$\Rightarrow$ $\Rightarrow$ Đường tròn có tâm I(2; 7) và bán kính R = 8.

b. Phương trình đường tròn có dạng ( $x - a)^{2} + (y - b)^{2} = R^{2}$ $x - a)^{2} + (y - b)^{2} = R^{2}$

$\Rightarrow$ $\Rightarrow$ Đường tròn có tâm I(-3; -2) và bán kính $R = 2\sqrt{2}.$ $R = 2\sqrt{2}.$

c. Phương trình có dạng $x^{2} + y^{2} - 2ax - 2by + c = 0 với a = 2, b = 3, c = -12$ $x^{2} + y^{2} - 2ax - 2by + c = 0 với a = 2, b = 3, c = -12$

Ta có: $a^{2} + b^{2} - c = 2^{2} + 3^{2} + 12 = 25$ $a^{2} + b^{2} - c = 2^{2} + 3^{2} + 12 = 25$

Vậy đường tròn có tâm I(2; 3) và bán kính $R = \sqrt{25} = 5.$ $R = \sqrt{25} = 5.$

Bài 7 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Lập phương trình đường tròn trong các trường hợp sau:

a. Có tâm I(-2; 4) và bán kính bằng 9;

b. Có tâm I(1; 2) và đi qua điểm A(4; 5);

c. Đi qua hai điểm A(4; 1), B(6; 5) và có tâm nằm trên đường thẳng 4x + y -16 = 0;

d. Đi qua gốc tọa độ và cắt hai trục tọa độ tại các điểm có hoành độ là a, tung độ là b.

Gợi ý đáp án

a. Phương trình đường tròn có tâm I(-2; 4) và bán kính R = 4 là:

$(x + 2)^{2} + (y - 4)^{2} = 16$ $(x + 2)^{2} + (y - 4)^{2} = 16$

b. Ta có $R = IA = \sqrt{(4 - 1)^{2} + (5 - 2)^{2}} = 3\sqrt{2}$ $R = IA = \sqrt{(4 - 1)^{2} + (5 - 2)^{2}} = 3\sqrt{2}$

Phương trình đường tròn có tâm I(1; 2) và bán kính $R = 3\sqrt{2}$ $R = 3\sqrt{2}$ là:

$(x - 1)^{2} + (y - 2)^{2} = 18$ $(x - 1)^{2} + (y - 2)^{2} = 18$

c. Phương trình đường tròn tâm I(a; b) có dạng: $x^{2} + y^{2} - 2ax - 2by + c = 0$ $x^{2} + y^{2} - 2ax - 2by + c = 0$

Vì I(a; b) thuộc đường thẳng 4x + y - 16 = 0 và các điểm A(4; 1), B(6; 5) thuộc đường tròn nên ta có hệ phương trình sau:

$\left\{\begin{matrix}4a + b - 16 = 0\\4^{2} + 1^{2} - 8a-2b +c = 0\\ 6^{2} + 5^{2} - 12a - 10b + c = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}4a + b - 16 = 0\\ 8a+2b -c = 17\\ 12a + 10b - c = 61\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}a = 3\\b = 4 \\ c = 15\end{matrix}\right.$ $\left\{\begin{matrix}4a + b - 16 = 0\\4^{2} + 1^{2} - 8a-2b +c = 0\\ 6^{2} + 5^{2} - 12a - 10b + c = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}4a + b - 16 = 0\\ 8a+2b -c = 17\\ 12a + 10b - c = 61\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}a = 3\\b = 4 \\ c = 15\end{matrix}\right.$

Vậy phương trình đường tròn là: $x^{2} + y^{2} - 6x - 8y + 15 = 0$ $x^{2} + y^{2} - 6x - 8y + 15 = 0$

d. Phương trình đường tròn (C) tâm I(m; n) có dạng: $x^{2} + y^{2} - 2mx - 2ny + c = 0$ $x^{2} + y^{2} - 2mx - 2ny + c = 0$

Vì O(0;0) \in (C) nên thay tọa độ O(0; 0) vào (C) ta được c = 0

Vì (C) cắt trục hoành tại điểm có tọa độ (a; 0) và cắt trục tung tại điểm có tọa độ (0; b) nên ta có:

$\left\{\begin{matrix}a^{2} - 2ma = 0\\b^{2} - 2nb = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} m = \frac{a}{2}\\n = \frac{b}{2}\end{matrix}\right. (vì a \neq 0, b\neq 0)$ $\left\{\begin{matrix}a^{2} - 2ma = 0\\b^{2} - 2nb = 0\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} m = \frac{a}{2}\\n = \frac{b}{2}\end{matrix}\right. (vì a \neq 0, b\neq 0)$

Vậy phương trình đường tròn (C) là: $x^{2} + y^{2} - ax - by = 0$ $x^{2} + y^{2} - ax - by = 0$

Bài 8 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Viết phương trình tiếp tuyến của đường tròn (C): $(x - 5)^{2} + (y - 3)^{2} = 100$ $(x - 5)^{2} + (y - 3)^{2} = 100$ tại điểm M(11; 11)

Gợi ý đáp án

Ta có: (C) có tâm I(5; 3).

Phương trình tiếp tuyến của đường tròn (C) tại M(11; 11) là:

$(5 - 11)(x - 11) + (3 - 11)(y - 11) = 0$

$\Leftrightarrow -6x - 8y + 154 = 0$ $\Leftrightarrow -6x - 8y + 154 = 0$

$\Leftrightarrow 3x + 4y - 77 = 0$ $\Leftrightarrow 3x + 4y - 77 = 0$

Bài 9 trang 73 SGK Toán 10 Chân trời sáng tạo Tập 2

Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip sau:

$a. \frac{x^{2}}{100} + \frac{y^{2}}{36} = 1;$ $a. \frac{x^{2}}{100} + \frac{y^{2}}{36} = 1;$

$b. \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1;$ $b. \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1;$

$c. x^{2} + 16y^{2} = 16$ $c. x^{2} + 16y^{2} = 16$

Gợi ý đáp án

$a. (E): \frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$ $a. (E): \frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

$\Rightarrow a = 10; b = 6 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{10^{2} - 6^{2}} = 8$ $\Rightarrow a = 10; b = 6 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{10^{2} - 6^{2}} = 8$

$\Rightarrow$ $\Rightarrow$ Tọa độ các tiêu điểm là: (-8; 0) và (8; 0)

Tọa độ các đỉnh là: (-10; 0), (10; 0), (0; -6); (0; 6)

Độ dài trục lớn bằng 2a = 2. 10 = 20; độ dài trục nhỏ bằng 2b = 2. 6 = 12.

$b. (E): \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ $b. (E): \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

$\Rightarrow a = 5; b = 4 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{5^{2} - 4^{2}} = 3$ $\Rightarrow a = 5; b = 4 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{5^{2} - 4^{2}} = 3$

$\Rightarrow$ $\Rightarrow$ Tọa độ các tiêu điểm là: (-3; 0) và (3; 0)

Tọa độ các đỉnh là: (-5; 0), (5; 0), (0; -4); (0; 4)

Độ dài trục lớn bằng 2a = 2. 5 = 10; độ dài trục nhỏ bằng 2b = 2. 4 = 8.

c. Ta có: $x^{2} + 16y^{2} = 16 \Leftrightarrow \frac{x^{2}}{16} + y^{2} = 1$ $x^{2} + 16y^{2} = 16 \Leftrightarrow \frac{x^{2}}{16} + y^{2} = 1$

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

$\Rightarrow a = 4; b = 1 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{4^{2} - 1^{2}} = \sqrt{15}$ $\Rightarrow a = 4; b = 1 \Rightarrow c = \sqrt{a^{2} - b^{2}} = \sqrt{4^{2} - 1^{2}} = \sqrt{15}$

$\Rightarrow$ $\Rightarrow$ Tọa độ các tiêu điểm là: $(-\sqrt{15}; 0) và (\sqrt{15}; 0)$ $(-\sqrt{15}; 0) và (\sqrt{15}; 0)$

Tọa độ các đỉnh là: (-4; 0), (4; 0), (0; -1); (0; 1)

Độ dài trục lớn bằng 2a = 2. 4 = 8; độ dài trục nhỏ bằng 2b = 2. 1 = 2.

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài tập cuối chương 9 CTST. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 10 CTST. Mời các bạn cùng tham khảo thêm tài liệu học tập môn Ngữ văn 10 CTST...