Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ CTST

Giải Toán 10 Tập 1 sách CTST

1 235

Tích vô hướng của hai vectơ

Bài 1 trang 101 SGK Toán 10 CTST
Bài 2 trang 101 SGK Toán 10 CTST
Bài 3 trang 101 SGK Toán 10 CTST
Bài 4 trang 101 SGK Toán 10 CTST
Bài 5 trang 101 SGK Toán 10 CTST
Bài 6 trang 101 SGK Toán 10 CTST

Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ CTST được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây nhé.

Bài 1 trang 101 SGK Toán 10 CTST

Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng:

$\overrightarrow {AB} .\overrightarrow {AD} ,\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {CB} ,\overrightarrow {AC} .\overrightarrow {BD}$

Gợi ý đáp án

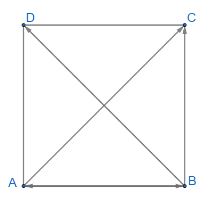
Ta có: $AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2$

+) $AB \bot AD \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0$

+) $\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a.\cos 45^\circ = \frac{{{a^2}\sqrt 2 }}{2}$

+) $\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.\cos 135^\circ = - {a^2}$

+) $AC \bot BD \Rightarrow \overrightarrow {AC} \bot \overrightarrow {BD} \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0$

Bài 2 trang 101 SGK Toán 10 CTST

Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:

$a) \overrightarrow {AB} .\overrightarrow {AO} ;$

$b) \overrightarrow {AB} .\overrightarrow {AD} .$

Gợi ý đáp án

$a) AC = BD = \sqrt {A{B^2} + A{D^2}} \\= \sqrt {{{\left( {2a} \right)}^2} + {a^2}} = a\sqrt 5$

$\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) = \cos \widehat {OAB} =\\ \cos \widehat {CAB} = \frac{{AB}}{{AC}} = \frac{{2a}}{{a\sqrt 5 }} = \frac{{2\sqrt 5 }}{5}$

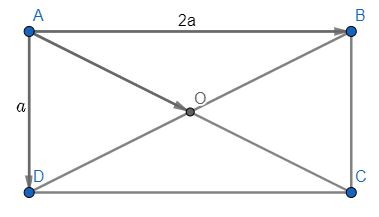
Giải Toán 10 Bài 4 CTST

$\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AO} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AO} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right) \\= AB.\frac{1}{2}AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AO} } \right)\\ = 2a.\frac{1}{2}.a\sqrt 5 .\frac{{2\sqrt 5 }}{5} = 2{a^2}\end{array}$

b) $AB \bot AD \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .$

Bài 3 trang 101 SGK Toán 10 CTST

Cho ba điểm O, A, B thẳng hàng và OA=a, OB=b. Tính tích vô hướng $\overrightarrow {OA} .\overrightarrow {OB}$ trong hai trường hợp:

a) Điểm O nằm ngoài đoạn thẳng AB;

b) Điểm O nằm trong đoạn thẳng AB

Gợi ý đáp án

a) Ta có:

Ta thấy hai vectơ $\overrightarrow {OA} và \overrightarrow {OB}$ cùng hướng nên $\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = 0^\circ$

$\Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = a.b.\cos 0^\circ = ab$

b) Ta có: Giải Toán 10 Bài 4 CTST

Ta thấy hai vectơ $\overrightarrow {OA}$ và $\overrightarrow {OB}$ ngược hướng nên $\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = 180^\circ$

$\Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = a.b.\cos 180^\circ = - ab$

Bài 4 trang 101 SGK Toán 10 CTST

Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng:

$\overrightarrow {MA} .\overrightarrow {MB} = {\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2}$

Gợi ý đáp án

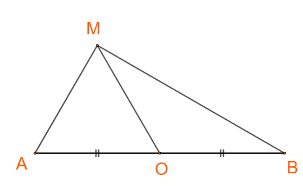
Ta có: $\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \Leftrightarrow - \overrightarrow {OA} = \overrightarrow {OB}$

$\Rightarrow {\overrightarrow {MO} ^2} - {\overrightarrow {OA} ^2} = \left( {\overrightarrow {MO} - \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) \\= \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) = \overrightarrow {MB} .\overrightarrow {MA} (đpcm)$

Bài 5 trang 101 SGK Toán 10 CTST

Một người dùng một lực $\overrightarrow F$ có độ lớn là 90 N làm một vật dịch chuyển một đoạn 100 m. Biết lực hợp $\overrightarrow F$ với hướng dịch chuyển là một góc $60^\circ$ . Tính công sinh bởi lực $\overrightarrow F$

Gợi ý đáp án

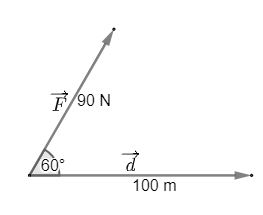
Công sinh bởi lực $\overrightarrow F$ được tính bằng công thức

$A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 90.100.\cos 60^\circ = 4500 (J)$

Vậy công sinh bởi lực $\overrightarrow F$ có độ lớn bằng 4500 (J)

Bài 6 trang 101 SGK Toán 10 CTST

Cho hai vectơ có độ dài lần lượt là 3 và 4 có tích vô hướng là - 6. Tính góc giữa hai vectơ đó.

Gợi ý đáp án

Ta cho: $\left| {\overrightarrow a } \right| = 3;\left| {\overrightarrow b } \right| = 4 và \overrightarrow a .\overrightarrow b = - 6$

Ta có công thức:

$\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 3.4.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)$

$\overrightarrow a .\overrightarrow b = - 6 \Rightarrow 3.4.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - 6 \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \frac{1}{2}$

$\Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 120^\circ$

VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ CTST. Mong rằng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán 10 CTST. Mời bạn đọc cùng tham khảo thêm môn Ngữ văn 10 CTST...

Đánh giá bài viết

1 235

Bài trước

Bài sau