Giải Toán 10 Bài 1: Dấu của tam thức bậc hai CTST

Toán 10 Chân trời sáng tạo tập 2

Giải Toán 10 Bài 1 CTST

Bài 1 trang 9 SGK Toán 10 Chân trời sáng tạo tập 2
Bài 2 trang 9 SGK Toán 10 Chân trời sáng tạo tập 2
Bài 3 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Bài 4 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Bài 5 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Bài 6 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Bài 7 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2
Bài 8 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2

Giải Toán 10 Bài 1: Dấu của tam thức bậc hai CTST được VnDoc.com tổng hợp và xin gửi tới bạn đọc. Mời các bạn cùng theo dõi chi tiết bài viết dưới đây nhé.

Bài 1 trang 9 SGK Toán 10 Chân trời sáng tạo tập 2

Đa thức nào sau đây là tam thức bậc hai?

$a. 4{{x}^{2}}+3x+1$ $a. 4{{x}^{2}}+3x+1$

$b. {{x}^{3}}+3{{x}^{2}}-1$ $b. {{x}^{3}}+3{{x}^{2}}-1$

$c. 2{{x}^{2}}+4x-1$ $c. 2{{x}^{2}}+4x-1$

Gợi ý đáp án

a. $4{{x}^{2}}+3x+1$ $4{{x}^{2}}+3x+1$ là tam thức bậc hai có a = 4; b = 3; c = 1

b. ${{x}^{3}}+3{{x}^{2}}-1$ ${{x}^{3}}+3{{x}^{2}}-1$ không là tam thức bậc hai

c. $2{{x}^{2}}+4x-1$ $2{{x}^{2}}+4x-1$ là tam thức bậc hai có a = 2; b = 4; c = -1

Bài 2 trang 9 SGK Toán 10 Chân trời sáng tạo tập 2

Xác định giá trị của m để các đa thức sau là tam thức bậc hai.

$a. (m+1){{x}^{2}}+2x+m$ $a. (m+1){{x}^{2}}+2x+m$

$b. m{{x}^{3}}+2{{x}^{2}}-x+m$ $b. m{{x}^{3}}+2{{x}^{2}}-x+m$

$c. -5{{x}^{2}}+2x-m+1$ $c. -5{{x}^{2}}+2x-m+1$

Gợi ý đáp án

Giá trị của m để các đa thức sau là tam thức bậc hai:

a. $(m+1){{x}^{2}}+2x+m$ $(m+1){{x}^{2}}+2x+m$ là tam thức bậc hai khi $m+1\ne 0\Leftrightarrow m\ne -1$ $m+1\ne 0\Leftrightarrow m\ne -1$

b. $m{{x}^{3}}+2{{x}^{2}}-x+m$ $m{{x}^{3}}+2{{x}^{2}}-x+m$ không là tam thức bậc hai.

c. $-5{{x}^{2}}+2x-m+1$ $-5{{x}^{2}}+2x-m+1$ là tam thức bậc hai với mọi m.

Bài 3 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2

Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng.

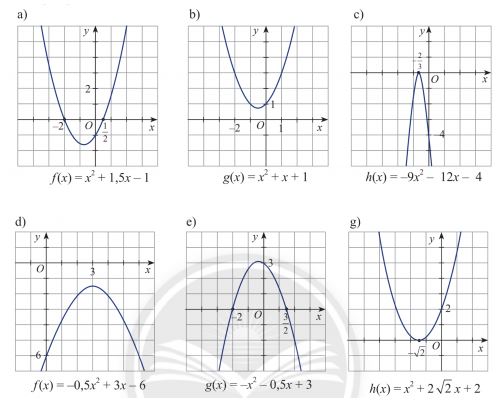
Giải Toán 10 Bài 1 CTST

Gợi ý đáp án

a. $f(x)={{x}^{2}}+1,5x-1 có \Delta =\frac{25}{4}>0$ $f(x)={{x}^{2}}+1,5x-1 có \Delta =\frac{25}{4}>0$, hai nghiệm phân biệt là ${{x}_{1}}=-2 ; {{x}_{2}}=\frac{1}{2} và a = 1 > 0$ ${{x}_{1}}=-2 ; {{x}_{2}}=\frac{1}{2} và a = 1 > 0$

Ta có bảng xét dấu f(x) như sau:

Giải Toán 10 Bài 1 CTST

Vậy f(x) dương trong hai khoảng $\left( -\infty ;\frac{1}{2} \right)$ $\left( -\infty ;\frac{1}{2} \right)$ và $\left( -2;+\infty \right)$ $\left( -2;+\infty \right)$ và âm trong khoảng $\left( \frac{1}{2};-2 \right).$ $\left( \frac{1}{2};-2 \right).$

b. $g(x)={{x}^{2}}+x+1$ $g(x)={{x}^{2}}+x+1$ có $\Delta =-3<0$ $\Delta =-3<0$ và a =1 >0 . Vậy f(x) dương với mọi $x\in \mathbb{R}$ $x\in \mathbb{R}$

c. $h(x)=-9{{x}^{2}}-12x-4$ $h(x)=-9{{x}^{2}}-12x-4$ có $\Delta = 0,$ $\Delta = 0,$ nghiệm kép là ${{x}_{o}}=\frac{-2}{3}$ ${{x}_{o}}=\frac{-2}{3}$ và a =-9<0.

Vậy f(x) âm với mọi $x\ne \frac{-2}{3}$ $x\ne \frac{-2}{3}$

d. $f(x)=-0,5{{x}^{2}}+3x-6$ $f(x)=-0,5{{x}^{2}}+3x-6$ có $\Delta =-3<0$ $\Delta =-3<0$ và a =-0,5 . Vậy f(x) âm với mọi $x\in \mathbb{R}$ $x\in \mathbb{R}$

e. $g(x)=-{{x}^{2}}-0,5x+3$ $g(x)=-{{x}^{2}}-0,5x+3$ có $\Delta =\frac{49}{4}>0$ $\Delta =\frac{49}{4}>0$ , hai nghiệm phân biệt là ${{x}_{1}}=-2 ; {{x}_{2}}=\frac{3}{2}$ ${{x}_{1}}=-2 ; {{x}_{2}}=\frac{3}{2}$ và a = -1 < 0

Ta có bảng xét dấu f(x) như sau:

Giải Toán 10 Bài 1 CTST

Vậy f(x) dương trong hai khoảng $\left( -\infty ;-2 \right)$ $\left( -\infty ;-2 \right)$ và $\left( \frac{3}{2};+\infty \right)$ $\left( \frac{3}{2};+\infty \right)$ và âm trong khoảng $\left( -2;\frac{3}{2} \right).$ $\left( -2;\frac{3}{2} \right).$

g. $h(x)={{x}^{2}}+2\sqrt{2}x+2 có \Delta = 0$ $h(x)={{x}^{2}}+2\sqrt{2}x+2 có \Delta = 0$, nghiệm kép là ${{x}_{o}}=-\sqrt{2}$ ${{x}_{o}}=-\sqrt{2}$ và a = -9 < 0.

Vậy f(x) âm với mọi $x\ne -\sqrt{2}$ $x\ne -\sqrt{2}$

Bài 4 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2

Xét dấu của tam thức bậc hai sau đây

$a. f(x) = 2x^{2} + 4x + 2$ $a. f(x) = 2x^{2} + 4x + 2$

$b. f(x) = -x^{2} + 2x + 21$ $b. f(x) = -x^{2} + 2x + 21$

$c. f(x) = -2x^{2} + x - 2$ $c. f(x) = -2x^{2} + x - 2$

$d. f(x) = -4x (x+3) - 9$

e. f(x) = (2x+5) (x-3)

Gợi ý đáp án

a. $\Delta = 4^{2} - 4.2.2 = 0$ $\Delta = 4^{2} - 4.2.2 = 0$. Và đa thức có nghiệm $x= \frac{-4}{2.2}=-1$ $x= \frac{-4}{2.2}=-1$

Mặt khác a= 2 > 0 nên f(x) luôn dương với mọi x khác -1

b. $\Delta = 2^{2} - 4(-3).21 = 256 > 0$ $\Delta = 2^{2} - 4(-3).21 = 256 > 0$ nên phương trình có hai nghiệm phân biệt : $x= \frac{-2-\sqrt{256}}{2.(-3)} = 3; x = \frac{-7}{3}$ $x= \frac{-2-\sqrt{256}}{2.(-3)} = 3; x = \frac{-7}{3}$ và a= -1 < 0 nên f(x) mang dấu âm khi x nằm trong khoảng $(\frac{-7}{3}; 3)$ $(\frac{-7}{3}; 3)$ và mang dấu dương với mọi x nằm ngoài khoảng $(\frac{-7}{3}; 3)$ $(\frac{-7}{3}; 3)$

c. $\Delta = (-2)^{2} - 4(-2)(-2)= -12< 0$ $\Delta = (-2)^{2} - 4(-2)(-2)= -12< 0$ và a= -2 < 0 nên f(x) luôn âm với mọi x

$d. f(x)= -4x^{2} - 12x -9$ $d. f(x)= -4x^{2} - 12x -9$.

$\Delta = (-12)^{2} - 4(-4)(-9) = 0$ $\Delta = (-12)^{2} - 4(-4)(-9) = 0$ nên có nghiệm kép là x = -1,5 và a= -4

\Rightarrow f(x) mang dấu âm với mọi x khác -1,5

e. f(x) = 2x^{2} - x - 15.

$\Delta = (-1)^{2} - 4.2.15= -119 < 0$ $\Delta = (-1)^{2} - 4.2.15= -119 < 0$, và a= 2 > 0 nên f(x) âm

Bài 5 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2

Độ cao ( tính bằng mét) của quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng theo hàm số $h(x) = -0,1x^{2} + x -1.$ $h(x) = -0,1x^{2} + x -1.$Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ, và ngang vành rổ. Làm tròn kết quả đến hàng phần mười.

Gợi ý đáp án

Hàm số h(x) có $\Delta = 1^{2} -4(-0,1)(-1) = 0,6 >0$ $\Delta = 1^{2} -4(-0,1)(-1) = 0,6 >0$ nên sẽ có hai nghiệm phân biệt : $x_{1} = 9, x_{2} = 1. và a = -0,1<0$ $x_{1} = 9, x_{2} = 1. và a = -0,1<0$

Vây :

Bóng nằm cao hơn vành rổ khi bóng nằm trong khoảng (1;9)
Bóng nằm thấp hơn vành rổ khi bóng nằm trong khoảng $(-\infty ; 1)$ $(-\infty ; 1)$ và $( 9; +\infty )$ $( 9; +\infty )$
Bóng nằm ngang vành rổ khi bóng ở độ cao 1m hoặc 9m

Bài 6 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2

Một khung dây thép hình chữ nhật có chiều dài 20cm và chiều rộng 15cm được uốn lại thành khung hình chữ nhật mới có kích thước (20 +x) và (15-x) cm. Với x nằm trong khoảng nào thì diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi.

Gợi ý đáp án

Diện tích của khung dây thép khi chưa uốn là : 20.15 = 300 ( $cm^{2}$ $cm^{2}$)

Diện tích của khung dây thép khi đã uốn là : $(20 + x). (15-x) = 300 - 5x - x^{2}$ $(20 + x). (15-x) = 300 - 5x - x^{2}$. Như vậy diện tích của khung sau khi uốn tùy thuộc vào giá trị của hàm số $f(x) = 5x + x^{2}.$ $f(x) = 5x + x^{2}.$

Xét hàm số f(x) có $\Delta = 5^{2} - 4.1.0 = 25 > 0 \Rightarrow$ $\Delta = 5^{2} - 4.1.0 = 25 > 0 \Rightarrow$có hai nghiệm phân biệt :

$x_{1} = \frac{-5-\sqrt{25}}{2. 1}= -5; x_{2} = \frac{-5+\sqrt{25}}{2. 1}= 0$ $x_{1} = \frac{-5-\sqrt{25}}{2. 1}= -5; x_{2} = \frac{-5+\sqrt{25}}{2. 1}= 0$ và có a = 1 > 0. Nên :

f(x) mang dấu dương khi x thuộc (-5;0) $\Rightarrow$ $\Rightarrow$ Diện tích khung hình sau khi uốn nhỏ hơn trước khi uốn (giảm đi )
f(x) mang dấu âm khi x thuộc $(-\infty ; -5) và (0 ; +\infty ) \Rightarrow$ $(-\infty ; -5) và (0 ; +\infty ) \Rightarrow$ Diện tích khung hình sau khi uốn lớn hơn trước khi uốn (tăng lên )
f(x) = 0 khi x = 0 hoặc x = -5 $\Rightarrow$ $\Rightarrow$ Diện tích khung hình sau khi uốn và trước khi uốn là không thay đổi

Bài 7 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2

Chứng minh rằng với mọi số thực m ta luôn có : $9m^{2} + 2m > -3$ $9m^{2} + 2m > -3$

Xét hàm số $f(m) = 9m^{2} + 2m + 3$ $f(m) = 9m^{2} + 2m + 3$. Ta có $\Delta = 2^{2}- 4.9.3 = -104 < 0$ $\Delta = 2^{2}- 4.9.3 = -104 < 0$ và có a = 9 > 0. Nên f(m) > 0 với mọi m nghĩa là $9m^{2} + 2m > 3$ $9m^{2} + 2m > 3$

Bài 8 trang 10 SGK Toán 10 Chân trời sáng tạo tập 2

Tìm giá trị của m để :

a $. 2x^{2} + 3x + m + 1 > 0$ $. 2x^{2} + 3x + m + 1 > 0$ với mọi $x\epsilon \mathbb{R}$ $x\epsilon \mathbb{R}$

b. $mx^{2} + 5x - 3 \leq 0$ $mx^{2} + 5x - 3 \leq 0$ với mọi $x\epsilon \mathbb{R}$ $x\epsilon \mathbb{R}$

Gợi ý đáp án

a. Hàm số $2x^{2} + 3x + m + 1$ $2x^{2} + 3x + m + 1$ có $\Delta = 3^{2} - 4.2(m+1) = 1- 8m$ $\Delta = 3^{2} - 4.2(m+1) = 1- 8m$. và a= 2 > 0 nên:

Để $2x^{2} + 3x + m + 1 > 0$ $2x^{2} + 3x + m + 1 > 0$ với mọi $x\epsilon \mathbb{R}$ $x\epsilon \mathbb{R}$ thì $\Delta < 0 \Rightarrow 1 - 8m < 0 \Rightarrow m> \frac{1}{8}$ $\Delta < 0 \Rightarrow 1 - 8m < 0 \Rightarrow m> \frac{1}{8}$

b. Xét hàm số $mx^{2} + 5x - 3$ $mx^{2} + 5x - 3$ có : $\Delta = 5^{2} - 4.m.(-3) = 25 + 12m$ $\Delta = 5^{2} - 4.m.(-3) = 25 + 12m$

Để $mx^{2} + 5x - 3 \leq 0$ $mx^{2} + 5x - 3 \leq 0$ với mọi $x\epsilon \mathbb{R} thì :$ $x\epsilon \mathbb{R} thì :$

$\Delta < 0$ $\Delta < 0$ và $m < 0 \Rightarrow m < \frac{-25}{12}$ $m < 0 \Rightarrow m < \frac{-25}{12}$

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 1: Dấu của tam thức bậc hai CTST. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán 10 CTST. Mời các bạn cùng tham khảo thêm tài liệu học tập môn Ngữ văn 10 CTST...