Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Bài tập cuối chương 5 CTST

Giải Toán 10 Tập 1 CTST

Bài trước

Bài sau

Bài tập cuối chương 5

Bài 1 trang 102 SGK Toán 10 CTST
Bài 2 trang 102 SGK Toán 10 CTST
Bài 3 trang 102 SGK Toán 10 CTST
Bài 4 trang 102 SGK Toán 10 CTST
Bài 5 trang 103 SGK Toán 10 CTST
Bài 6 trang 103 SGK Toán 10 CTST
Bài 7 trang 103 SGK Toán 10 CTST
Bài 8 trang 103 SGK Toán 10 CTST
Bài 9 trang 103 SGK Toán 10 CTST

Bài tập cuối chương 5 CTST được VnDoc.com tổng hợp và xin gửi tới bạn đọc. Bài viết sẽ hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 CTST. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

Bài 1 trang 102 SGK Toán 10 CTST

Cho 3 vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$đều khác vectơ $\overrightarrow 0$ $\overrightarrow 0$ . Các khẳng định sau đúng hay sai?

a) Nếu hai vectơ $\overrightarrow a ,\overrightarrow b$ $\overrightarrow a ,\overrightarrow b$cùng phương với $\overrightarrow c thì \overrightarrow a$ $\overrightarrow c thì \overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$cùng phương

b) Nếu hai vectơ $\overrightarrow a ,\overrightarrow b$ $\overrightarrow a ,\overrightarrow b$cùng ngược hướng với $\overrightarrow c$ $\overrightarrow c$thì $\overrightarrow a$ $\overrightarrow a$và $\overrightarrow b$ $\overrightarrow b$cùng hướng

Gợi ý đáp án

+) Vectơ $\overrightarrow a$ $\overrightarrow a$ cùng phương với vectơ $\overrightarrow c$ $\overrightarrow c$nên giá của vectơ $\overrightarrow a$ $\overrightarrow a$song song với giá của vectơ $\overrightarrow{c}$ $\overrightarrow{c}$

+) Vectơ $\overrightarrow b$ $\overrightarrow b$cùng phương với vectơ $\overrightarrow c$ $\overrightarrow c$ nên giá của vectơ $\overrightarrow b$ $\overrightarrow b$song song với giá của vectơ $\overrightarrow c$ $\overrightarrow c$

Suy ra giá của vectơ $\overrightarrow a$ $\overrightarrow a$và vectơ $\overrightarrow b$ $\overrightarrow b$song song với nhau nên $\overrightarrow a$ $\overrightarrow a$và $\overrightarrow b$ $\overrightarrow b$cùng phương

Vậy khẳng định trên đúng

b) Giả sử vectơ $\overrightarrow c$ $\overrightarrow c$có hướng từ A sang B

+) Vectơ $\overrightarrow a$ $\overrightarrow a$ngược hướng với vectơ $\overrightarrow c$ $\overrightarrow c$nên giá của vectơ $\overrightarrow a$ $\overrightarrow a$song song với giá của vectơ $\overrightarrow c$ $\overrightarrow c$và có hướng từ B sang A

+) Vectơ $\overrightarrow b$ $\overrightarrow b$ngược hướng với vectơ $\overrightarrow c$ $\overrightarrow c$ nên giá của vectơ $\overrightarrow b$ $\overrightarrow b$ song song với giá của vectơ $\overrightarrow c$ $\overrightarrow c$ và có hướng từ B sang A

Suy ra, hai vectơ $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$ cùng hướng

Vậy khẳng định trên đúng

Bài 2 trang 102 SGK Toán 10 CTST

Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a.

a) Tính độ dài các vectơ $\overrightarrow {AC} ,\overrightarrow {BD}$ $\overrightarrow {AC} ,\overrightarrow {BD}$

b) Tìm trong hình ảnh vectơ đối nhau và có độ dài bằng $\frac{{a\sqrt {10} }}{2}$ $\frac{{a\sqrt {10} }}{2}$

Gợi ý đáp án

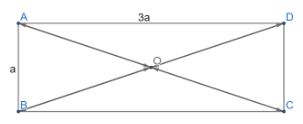
a) Ta có:

$AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {3a} \right)}^2}} = a\sqrt {10}$ $AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {3a} \right)}^2}} = a\sqrt {10}$

$+) \left| {\overrightarrow {AC} } \right| = AC = a\sqrt {10}$ $+) \left| {\overrightarrow {AC} } \right| = AC = a\sqrt {10}$

$+) \left| {\overrightarrow {BD} } \right| = BD = a\sqrt {10}$ $+) \left| {\overrightarrow {BD} } \right| = BD = a\sqrt {10}$

b) O là giao điểm của hai đường chéo nên ta có:

$AO = OC = BO = OD = \frac{{a\sqrt {10} }}{2}$ $AO = OC = BO = OD = \frac{{a\sqrt {10} }}{2}$

Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng

Suy ra các cặp vectơ đối nhau và có độ dài bằng $\frac{{a\sqrt {10} }}{2}$ $\frac{{a\sqrt {10} }}{2}$ là:

$\overrightarrow {OA} và \overrightarrow {OC} ; \overrightarrow {AO} và \overrightarrow {CO} ; \overrightarrow {OB} và \overrightarrow {OD} ; \overrightarrow {BO} và \overrightarrow {DO}$ $\overrightarrow {OA} và \overrightarrow {OC} ; \overrightarrow {AO} và \overrightarrow {CO} ; \overrightarrow {OB} và \overrightarrow {OD} ; \overrightarrow {BO} và \overrightarrow {DO}$

Bài 3 trang 102 SGK Toán 10 CTST

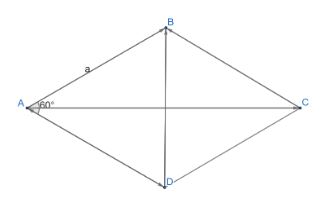
Cho hình thoi ABCD đi có cạnh bằng a và có góc A bằng $60^\circ$ $60^\circ$ . Tìm độ dài của các vectơ sau: $\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} ;\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} ;\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} .$ $\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} ;\overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} ;\overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} .$

Gợi ý đáp án

+) ABCD là hình thoi nên cũng là hình bình hành

Áp dụng quy tắc hình bình hành ta có:

$\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$ $\overrightarrow p = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$

$+) \overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB}$ $+) \overrightarrow u = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB}$

$+) \overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {AB} + \left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \overrightarrow {AB} + \overrightarrow {CB} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB}$ $+) \overrightarrow v = 2\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {AB} + \left( {\overrightarrow {AB} - \overrightarrow {AC} } \right) = \overrightarrow {AB} + \overrightarrow {CB} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB}$

Bài tập cuối chương 5 CTST

Bài 4 trang 102 SGK Toán 10 CTST

Cho hình bình hành ABCD hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho $\overrightarrow {CE} = \overrightarrow {AN}$ $\overrightarrow {CE} = \overrightarrow {AN}$ (hình 1)

a) Tìm tổng của các vectơ:

$\overrightarrow {NC} và \overrightarrow {MC} ; \overrightarrow {AM} và \overrightarrow {CD} ; \overrightarrow {AD} và \overrightarrow {NC}$ $\overrightarrow {NC} và \overrightarrow {MC} ; \overrightarrow {AM} và \overrightarrow {CD} ; \overrightarrow {AD} và \overrightarrow {NC}$

b) Tìm các vectơ hiệu:

$\overrightarrow {NC} - \overrightarrow {MC} ; \overrightarrow {AC} - \overrightarrow {BC} ; \overrightarrow {AB} - \overrightarrow {ME} .$ $\overrightarrow {NC} - \overrightarrow {MC} ; \overrightarrow {AC} - \overrightarrow {BC} ; \overrightarrow {AB} - \overrightarrow {ME} .$

c) Chứng minh $\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD}$ $\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD}$

Gợi ý đáp án

a) Ta có: $\overrightarrow {CE} = \overrightarrow {AN} \Rightarrow CE//AN và CE = AN = ND = BM = MC$ $\overrightarrow {CE} = \overrightarrow {AN} \Rightarrow CE//AN và CE = AN = ND = BM = MC$

Suy ra $\overrightarrow {MC} = \overrightarrow {CE}$ $\overrightarrow {MC} = \overrightarrow {CE}$

$+) \overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CE} = \overrightarrow {NE}$ $+) \overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CE} = \overrightarrow {NE}$

+) ABCD là hình bình hành nên $\overrightarrow {CD} = \overrightarrow {BA}$ $\overrightarrow {CD} = \overrightarrow {BA}$

$\overrightarrow {AM} + \overrightarrow {CD} = \overrightarrow {AM} + \overrightarrow {BA} = \overrightarrow {BM}$ $\overrightarrow {AM} + \overrightarrow {CD} = \overrightarrow {AM} + \overrightarrow {BA} = \overrightarrow {BM}$

+) Ta có $\overrightarrow {MC} = \overrightarrow {AN} \Rightarrow AMCN$ $\overrightarrow {MC} = \overrightarrow {AN} \Rightarrow AMCN$ là hình bình hành nên $\overrightarrow {NC} = \overrightarrow {AM}$ $\overrightarrow {NC} = \overrightarrow {AM}$

$\overrightarrow {AD} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {AM} = \overrightarrow {AE}$ $\overrightarrow {AD} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {AM} = \overrightarrow {AE}$ (vì AMED là hình bình hành)

b) Ta có:

$+) \overrightarrow {NC} - \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CM} = \overrightarrow {NM}$ $+) \overrightarrow {NC} - \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CM} = \overrightarrow {NM}$

$+) \overrightarrow {AC} - \overrightarrow {BC} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB}$ $+) \overrightarrow {AC} - \overrightarrow {BC} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB}$

$+) \overrightarrow {AB} - \overrightarrow {ME} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB}$ $+) \overrightarrow {AB} - \overrightarrow {ME} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB}$

c) Ta có:

$\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AM} + \overrightarrow {MC} = \overrightarrow {AC}$ $\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AM} + \overrightarrow {MC} = \overrightarrow {AC}$

Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có

$\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$ $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$

Từ đó suy ra $\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD}$ $\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD}$(đpcm)

Bài 5 trang 103 SGK Toán 10 CTST

Cho $\overrightarrow a ,\overrightarrow b$ $\overrightarrow a ,\overrightarrow b$ là hai vectơ khác vectơ \overrightarrow 0 . Trong trường hợp nào thì đẳng thức sau đúng?

$a) \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|;$ $a) \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|;$

$b) \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a - \overrightarrow b } \right| .$ $b) \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a - \overrightarrow b } \right| .$

Gợi ý đáp án

$a) \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \Leftrightarrow {\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left( {\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|} \right)^2}$ $a) \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \Leftrightarrow {\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left( {\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|} \right)^2}$

$\Leftrightarrow {\left( {\overrightarrow a + \overrightarrow b } \right)^2} = {\left( {\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|} \right)^2} \Leftrightarrow {\left( {\overrightarrow a } \right)^2} + 2\overrightarrow a .\overrightarrow b + {\left( {\overrightarrow b } \right)^2}$ $\Leftrightarrow {\left( {\overrightarrow a + \overrightarrow b } \right)^2} = {\left( {\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|} \right)^2} \Leftrightarrow {\left( {\overrightarrow a } \right)^2} + 2\overrightarrow a .\overrightarrow b + {\left( {\overrightarrow b } \right)^2}$

$= {\left| {\overrightarrow a } \right|^2} + 2.\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| + {\left| {\overrightarrow b } \right|^2}$ $= {\left| {\overrightarrow a } \right|^2} + 2.\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| + {\left| {\overrightarrow b } \right|^2}$

$\Leftrightarrow {\left| {\overrightarrow a } \right|^2} + 2\overrightarrow a .\overrightarrow b + {\left| {\overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + 2.\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| + {\left| {\overrightarrow b } \right|^2}$ $\Leftrightarrow {\left| {\overrightarrow a } \right|^2} + 2\overrightarrow a .\overrightarrow b + {\left| {\overrightarrow b } \right|^2} = {\left| {\overrightarrow a } \right|^2} + 2.\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| + {\left| {\overrightarrow b } \right|^2}$

$\Leftrightarrow 2\overrightarrow a .\overrightarrow b = 2\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|$ $\Leftrightarrow 2\overrightarrow a .\overrightarrow b = 2\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|$

$\Leftrightarrow 2\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 2\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|$ $\Leftrightarrow 2\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 2\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|$

$\Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 1 \Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 0^\circ$ $\Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 1 \Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 0^\circ$

Vậy $\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \Leftrightarrow \overrightarrow a , \,\overrightarrow b$ $\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| \Leftrightarrow \overrightarrow a , \,\overrightarrow b$ cùng hướng.

$b) \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a - \overrightarrow b } \right| \Leftrightarrow {\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a - \overrightarrow b } \right|^2}$ $b) \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a - \overrightarrow b } \right| \Leftrightarrow {\left| {\overrightarrow a + \overrightarrow b } \right|^2} = {\left| {\overrightarrow a - \overrightarrow b } \right|^2}$

$\Leftrightarrow {\left( {\overrightarrow a + \overrightarrow b } \right)^2} = {\left( {\overrightarrow a - \overrightarrow b } \right)^2}$ $\Leftrightarrow {\left( {\overrightarrow a + \overrightarrow b } \right)^2} = {\left( {\overrightarrow a - \overrightarrow b } \right)^2}$

$\Leftrightarrow {\left( {\overrightarrow a } \right)^2} + 2\overrightarrow a .\overrightarrow b + {\left( {\overrightarrow b } \right)^2} = {\left( {\overrightarrow a } \right)^2} - 2\overrightarrow a .\overrightarrow b + {\left( {\overrightarrow b } \right)^2}$ $\Leftrightarrow {\left( {\overrightarrow a } \right)^2} + 2\overrightarrow a .\overrightarrow b + {\left( {\overrightarrow b } \right)^2} = {\left( {\overrightarrow a } \right)^2} - 2\overrightarrow a .\overrightarrow b + {\left( {\overrightarrow b } \right)^2}$

$\Leftrightarrow 2\overrightarrow a .\overrightarrow b = - 2\overrightarrow a .\overrightarrow b \Leftrightarrow 4\overrightarrow a .\overrightarrow b = 0$ $\Leftrightarrow 2\overrightarrow a .\overrightarrow b = - 2\overrightarrow a .\overrightarrow b \Leftrightarrow 4\overrightarrow a .\overrightarrow b = 0$

$\Leftrightarrow \overrightarrow a .\overrightarrow b = 0 \Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ$ $\Leftrightarrow \overrightarrow a .\overrightarrow b = 0 \Leftrightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 90^\circ$

Vậy $\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a - \overrightarrow b } \right| \Leftrightarrow \overrightarrow a ,\overrightarrow b$ $\left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a - \overrightarrow b } \right| \Leftrightarrow \overrightarrow a ,\overrightarrow b$ vuông góc với nhau.

Bài 6 trang 103 SGK Toán 10 CTST

Cho $\left| {\overrightarrow a + \overrightarrow b } \right| = 0$ $\left| {\overrightarrow a + \overrightarrow b } \right| = 0$. So sánh độ dài, phương và hướng của hai vectơ $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b .$ $\overrightarrow b .$

Gợi ý đáp án

$\left| {\overrightarrow a + \overrightarrow b } \right| = 0 \Leftrightarrow \overrightarrow a + \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow a = - \overrightarrow b$ $\left| {\overrightarrow a + \overrightarrow b } \right| = 0 \Leftrightarrow \overrightarrow a + \overrightarrow b = \overrightarrow 0 \Leftrightarrow \overrightarrow a = - \overrightarrow b$

$\overrightarrow a = - \overrightarrow b$ $\overrightarrow a = - \overrightarrow b$ suy ra hai vectơ $\overrightarrow a$ $\overrightarrow a$ và $\overrightarrow b$ $\overrightarrow b$là hai vecto đối nhau nên chúng cùng phương, ngược hướng và có độ dài bằng nhau.

Bài 7 trang 103 SGK Toán 10 CTST

Cho bốn điểm A, B, C, D. Chứng minh rằng $\overrightarrow {AB} = \overrightarrow {CD}$ $\overrightarrow {AB} = \overrightarrow {CD}$ khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.

Gợi ý đáp án

Với 4 điểm A, B, C, D ta có: $\overrightarrow {AB} = \overrightarrow {CD}$ $\overrightarrow {AB} = \overrightarrow {CD}$ khi và chỉ khi tứ giác ABDC là hình bình hành

Theo tính chất của hình bình hành thì giao điểm của hai đường chéo là trung điểm của mỗi đường và ngược lại.

Nói cách khác: trung điểm của hai đoạn thẳng AD và BC trùng nhau.

Vậy ta có điều phải chứng minh.

Bài 8 trang 103 SGK Toán 10 CTST

Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng $\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0$ $\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0$ .

Gợi ý đáp án

$\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)$ $\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)$

$= \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0$ $= \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0$ (đpcm)

Bài 9 trang 103 SGK Toán 10 CTST

Một chiếc máy bay được biết là đang bay về phía Bắc với tốc độ 45m/s, mặc dù vận tốc của nó so với mặt đất là 38 m/s theo hướng nghiêng một góc $20^\circ$ $20^\circ$ về phía tây bắc (hình 2). Tính tốc độ của gió

Gợi ý đáp án

Từ giả thiết ta có:

+) Vectơ tương ứng với vận tốc máy bay là vectơ $\overrightarrow {{v_1}}$ $\overrightarrow {{v_1}}$

+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ $\overrightarrow v$ $\overrightarrow v$

+) Vectơ tương ứng với vận tốc gió là vectơ $\overrightarrow {{v_2}}$ $\overrightarrow {{v_2}}$

Ta có : $\left| {\overrightarrow {{v_1}} } \right| = 45;\left| {\overrightarrow v } \right| = 38;\left( {\overrightarrow {{v_1}} ,\overrightarrow v } \right) = 20^\circ$ $\left| {\overrightarrow {{v_1}} } \right| = 45;\left| {\overrightarrow v } \right| = 38;\left( {\overrightarrow {{v_1}} ,\overrightarrow v } \right) = 20^\circ$

Áp dụng định lý cosin ta có:

$\left| {\overrightarrow {{v_2}} } \right| = \sqrt {{{\left| {\overrightarrow v } \right|}^2} + {{\left| {\overrightarrow {{v_1}} } \right|}^2} - 2\left| {\overrightarrow v } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow v ,\overrightarrow {{v_1}} } \right)}$ $\left| {\overrightarrow {{v_2}} } \right| = \sqrt {{{\left| {\overrightarrow v } \right|}^2} + {{\left| {\overrightarrow {{v_1}} } \right|}^2} - 2\left| {\overrightarrow v } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow v ,\overrightarrow {{v_1}} } \right)}$

$= \sqrt {{{38}^2} + {{45}^2} - 2.38.45.\cos 20^\circ } \simeq 16 (m/s)$ $= \sqrt {{{38}^2} + {{45}^2} - 2.38.45.\cos 20^\circ } \simeq 16 (m/s)$

Vậy tốc độ của gió gần bằng 16 m/s

Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Bài tập cuối chương 5 CTST. Hi vọng qua đây bạn đọc có thêm tài liệu học tập nhé. Mời các bạn cùng tham khảo thêm tài liệu học tập môn Ngữ văn 10 CTST...

Chia sẻ, đánh giá bài viết

178

Bài trước

Bài sau