Giải Toán 10 Bài 1: Khái niệm vectơ CTST
Khái niệm vectơ
VnDoc.com xin gửi tới bạn đọc bài viết Giải Toán 10 Bài 1: Khái niệm vectơ CTST để bạn đọc cùng tham khảo. Bài viết sẽ hướng dẫn bạn đọc trả lời các câu hỏi trong SGK Toán 10 CTST. Mời bạn đọc cùng theo dõi bài viết dưới đây nhé.
Bài 1 trang 86 SGK Toán 10 CTST
a) Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
- Bác Ba có số tiền 20 triệu đồng
- Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc.
b) Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?
Giá tiền, lực, thể tích, tuổi, độ dịch chuyển, vận tốc
Gợi ý đáp án
a) Sự khác biệt là:
- Đơn vị của 2 đại lượng: triệu đồng và km/h
- 20 triệu đồng là 1 đại lượng vô hướng còn cơn bão là đại lượng có hướng cụ thể là hướng từ đông sang bắc với vận tốc là 20 km/h
b) Các đại lượng cần biểu diễn vectơ là các đại lượng có hướng nên đó là: lực, độ dịch chuyển, vận tốc.
Bài 2 trang 86 SGK Toán 10 CTST
Cho hình thang ABCD có hai cạnh đáy là AB và DC (hình 15). Điểm M nằm trên đoạn DC.
a) Gọi tên các vectơ cùng hướng với vectơ 
\(\overrightarrow {AB}\)
b) Gọi tên các vectơ ngược hướng với vectơ \(\overrightarrow {DM}\)
Gợi ý đáp án
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ \(\overrightarrow {AB}\) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC}\)
b)\(\overrightarrow {DM}\) có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM}\) là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD}\)
Bài 3 trang 86 SGK Toán 10 CTST
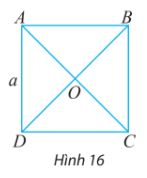
Cho hình vuông ABCD có tâm O và có các cạnh bằng a (hình 16)
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\)
Gợi ý đáp án
\(a) AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2\)
\(\Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:
\(\overrightarrow {AO}\)và\(\overrightarrow {AO}\); \(\overrightarrow {CO}\)và \(\overrightarrow {OA} ; \overrightarrow {DO}\) và \(\overrightarrow {OB} ; \overrightarrow {OD} và \overrightarrow {BO}\)
b) Các cặp vectơ đối nhau và có độ dài bằng \(\frac{a\sqrt{2}}{2}\)
\(\overrightarrow {AO}\) và \(\overrightarrow {CO}\); \(\overrightarrow {OA}\)và \(\overrightarrow {OC} ; \overrightarrow {OB}\) và \(\overrightarrow {OD} ; \overrightarrow {BO}\) và \(\overrightarrow {DO}\)
Bài 4 trang 86 SGK Toán 10 CTST
Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC}\)
Gợi ý đáp án
Tứ giác ABCD là hình bình hành
\(\Leftrightarrow \left\{ \begin{array}{l} AB // DC\\ AB = DC \end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC}\)cùng phương, do đó cùng hướng.
\(\Leftrightarrow \left\{ \begin{array}{l} \overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\ AB = DC \end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC}\)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} .\)
Bài 5 trang 86 SGK Toán 10 CTST
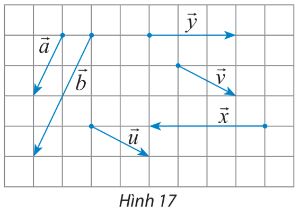
Hãy chỉ ra các cặp vectơ cùng hướng, ngược hướng, bằng nhau trong hình 17.
Gợi ý đáp án
+ Các cặp vectơ cùng hướng là: \(\overrightarrow a và \overrightarrow b ; \overrightarrow u và \overrightarrow v\)
+ Các cặp vectơ ngược hướng là:\(\overrightarrow x và \overrightarrow y\)
+ Các cặp vectơ bằng nhau là: \(\overrightarrow u và \overrightarrow v\)
Bài 6 trang 87 SGK Toán 10 CTST
Đề bài
Gọi O là tâm hình lục giác đều ABCDEF.
a) Tìm các vectơ khác vectơ \(\overrightarrow 0\)và cùng hướng với vectơ \(\overrightarrow {OA} .\)
b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} .\)
Gợi ý đáp án
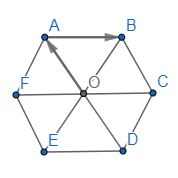
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ \(\overrightarrow 0\)và cùng hướng với vectơ \(\overrightarrow {OA}\) là : \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF}\)
b) Ta có: OA = OB = OC = OD = OE = FO và AB // EC // ED
Suy ra các vectơ bằng vectơ \(\overrightarrow {AB}\) là \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED}\)
Bài 7 trang 87 SGK Toán 10 CTST
Tìm các lực cùng hướng và ngược hướng trong số các lực đẩy được biểu diễn bằng các vectơ trong hình 18
Gợi ý đáp án
Nhận xét: giá của 4 lực đều song song hoặc trùng nhau, do đó 4 vectơ là cùng phương.
Vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\)có chiều từ phải sang trái còn vectơ \(\overrightarrow d\)có chiều từ trái sang phải
Vậy các vectơ (hay lực) cùng hướng với nhau là vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c .\)
Các vectơ (lực) \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c\)ngược hướng với vectơ \(\overrightarrow d .\)
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Giải Toán 10 Bài 1: Khái niệm vectơ CTST. Mong rằng qua đây bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán 10 CTST. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn 10 CTST...
