Toán 10 Bài 4 Bất phương trình bậc nhất hai ẩn
Bất phương trình bậc nhất hai ẩn Toán 10
Toán 10 Bài 4: Bất phương trình bậc nhất hai ẩn được VnDoc biên soạn bao gồm hướng dẫn lý thuyết và giải cho từng bài tập trong 3 bộ sách giáo khoa lớp 10 mới. Mời các bạn cùng tham bảo bài viết dưới đây
Giải Toán 10 Bài Bất phương trình bậc nhất hai ẩn sách mới
1. Giải Toán 10 bài Bất phương trình bậc nhất hai ẩn CTST
Mời bạn đọc cùng tham khảo thêm tại Giải Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn CTST
Bài 1 trang 32 SGK Toán 10 CTST Tập 1
Cho bất phương trình bậc nhất hai ẩn x - 2y + 6 > 0.
a) (0 ; 0) có phải là một nghiệm của bất phương trình đã cho không?
b) Chỉ ra ba cặp số (x ; y) là nghiệm của bất phương trình đã cho.
c) Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng tọa độ Oxy.
Lời giải
a) Với cặp (0 ; 0) ta có : 0 – 2.0 + 6 = 6 > 0 nên (0 ; 0) là nghiệm của bất phương trình đã cho.
Vậy (0 ; 0) là một nghiệm của bất phương trình x - 2y + 6 > 0.
b)
+ Lấy cặp số (1 ; 0) ta có 1 – 2.0 + 6 = 7 > 0 nên cặp số (1 ; 0) là một nghiệm của bất phương trình x - 2y + 6 > 0.
+ Lấy cặp số (0 ; 1) ta có 0 – 2.1 + 6 = 4 > 0 nên cặp số (0 ; 1) là một nghiệm của bất phương trình x - 2y + 6 > 0.
+ Lấy cặp số (-1 ; -1) ta có –1 – 2. (–1) + 6 = 7 > 0 nên cặp số (-1 ; -1) là một nghiệm của bất phương trình x - 2y + 6 > 0.
Vậy ta có ba cặp số (1 ; 0) ; (0 ; 1) ; (-1 ; -1) đều là nghiệm của bất phương trình x - 2y + 6 > 0.
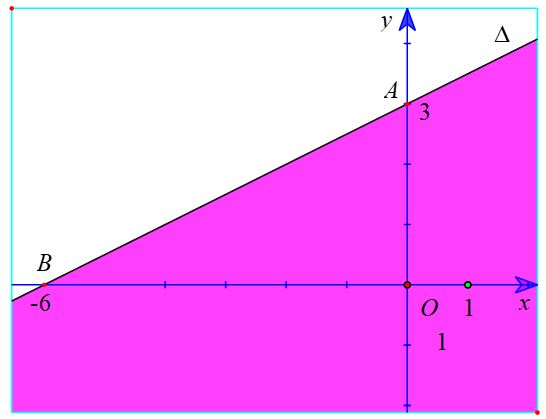
c) Vẽ đường thẳng ∆ : x – 2y + 6 = 0 đi qua hai điểm A(0; 3); B(-6; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và (0 ; 0) là một nghiệm của bất phương trình
x - 2y + 6 > 0.
Do đó, miền nghiệm của bất phương trình x - 2y + 6 > 0 là nửa mặt phẳng không kể bờ ∆, chứa điểm O (là miền được tô màu trong hình sau).
Bài 2 trang 32 SGK Toán 10 CTST Tập 1
Biểu diễn tập nghiệm của các bất phương trình sau trên mặt phẳng tọa độ Oxy.
a) – x + y + 2 > 0
b) y + 2 ≥ 0
c ) – x + 2 ≤ 0.
Lời giải
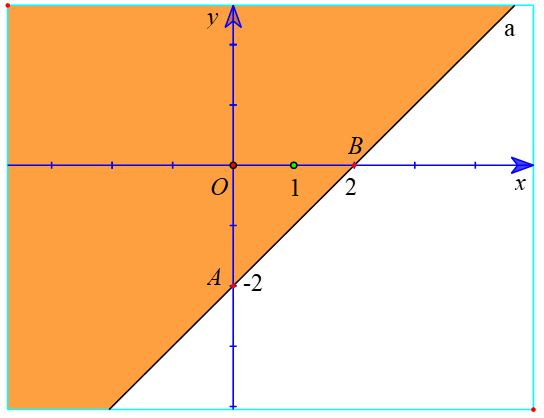
a) Vẽ đường thẳng a: – x + y + 2 = 0 đi qua hai điểm A (0; - 2); B (2; 0).
Xét gốc tọa độ O (0 ; 0). Ta thấy O ∉ a và – 0 + 0 + 2 = 2 > 0.
Suy ra (0 ; 0) là một nghiệm của bất phương trình – x + y + 2 > 0.
Do đó, miền nghiệm của bất phương trình – x + y + 2 > 0 là nửa mặt phẳng không kể bờ a, chứa điểm O (là miền tô màu trong hình sau).
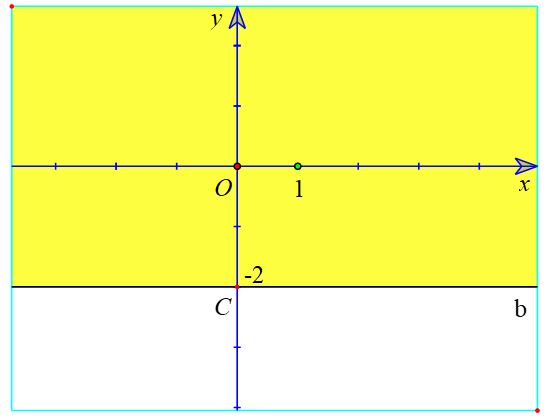
b) Vẽ đường thẳng b: y + 2 = 0 đi qua điểm C (0; -2) và song song với trục Ox
Xét gốc tọa độ O (0 ; 0). Ta thấy O ∉ b và 0 + 2 = 2 > 0
Suy ra (0 ; 0) là nghiệm của bất phương trình y + 2 ≥ 0.
Do đó, miền nghiệm của bất phương trình y + 2 ≥ 0 là nửa mặt phẳng kể cả bờ b, chứa điểm O (là miền tô màu vàng trong hình sau).
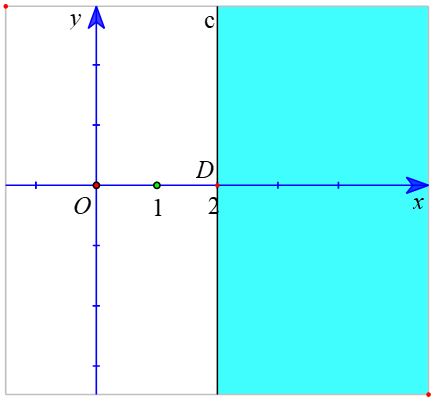
c) ) Vẽ đường thẳng c : – x + 2 = 0.đi qua điểm D (2; 0) và song song với trục Oy.
Xét gốc tọa độ O (0 ; 0). Ta thấy O ∉ c và – 0 + 2 = 2 > 0
Suy ra (0 ; 0) không là nghiệm của bất phương trình – x + 2 ≤ 0.
Do đó, miền nghiệm của bất phương trình – x + 2 ≤ 0.là nửa mặt phẳng kể cả bờ c, không chứa điểm O (là miền tô màu xanh trong hình sau).
Bài 3 trang 32 SGK Toán 10 CTST Tập 1
Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ oxy
a) – x + 2 + 2 (y – 2) < 2 (1 – x)
b) 3(x – 1 ) + 4(y – 2) < 5x – 3.
Lời giải
a) Ta có: – x + 2 + 2(y – 2 ) < 2(1 – x)
⇔ – x + 2 + 2(y – 2 ) – 2(1 – x) < 0
⇔ – x + 2 + 2y – 4 – 2 + 2x < 0
⇔ x + 2y – 4 < 0
Ta sẽ biểu diễn miền nghiệm của bất phương trình x + 2y – 4 < 0.
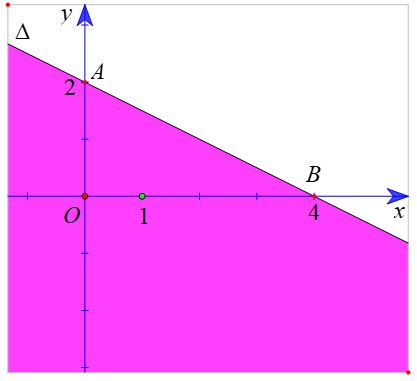
Vẽ đường thẳng ∆: x + 2y – 4 = 0 đi qua điểm A (0; 2) và B (4 ; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆ và 0 + 2.0 – 4 = – 4 < 0.
Suy ra (0 ; 0) là nghiệm của bất phương trình x + 2y – 4 < 0.
Do đó, miền nghiệm của bất phương trình x + 2y – 4 < 0 là nửa mặt phẳng không kể bờ ∆, chứa điểm O (là miền tô màu trong hình sau).
b) Ta có: 3(x – 1 ) + 4(y – 2) < 5x – 3
⇔ 3x – 3 + 4y – 8 – 5x + 3 < 0
⇔ – 2x + 4y – 8 < 0
⇔ – x + 2y – 4 < 0
Ta sẽ biểu diễn miền nghiệm của bất phương trình – x + 2y – 4 < 0
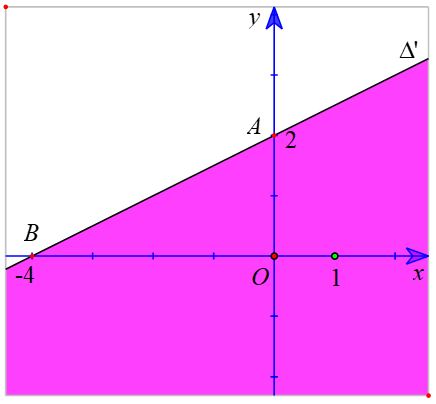
Vẽ đường thẳng ∆’ : – x + 2y – 4 = 0 đi qua điểm A(0; 2) và B (– 4 ; 0).
Xét gốc tọa độ O(0 ; 0). Ta thấy O ∉ ∆’ và – 0 + 2. 0 – 4 = – 4 < 0.
Suy ra (0 ; 0) là nghiệm của bất phương trình – x + 2y – 4 < 0.
Do đó, miền nghiệm của bất phương trình –x + 2y – 4 < 0 là nửa mặt phẳng không kể bờ ∆’, chứa điểm O (là miền tô màu trong hình sau).
Bài 4 trang 32 SGK Toán 10 CTST Tập 1
Bạn Cúc muốn pha hai loại nước cam. Để pha một lít nước cam loại I cần 30 g bột cam, còn một lít nước cam loại II cần 20 g bột cam. Gọi x và y lần lượt là số lít nước cam loại I và II pha chế được. Biết rằng Cúc chỉ có thể dùng không quá 100 g bột cam. Hãy lập các bất phương trình mô tả số lít nước cam loại I và II mà bạn Cúc có thể pha chế được và biểu diễn miền nghiệm của các bất phương trình đó trên cùng một mặt phẳng tọa độ Oxy.
Lời giải
Vì x, y là là số lít nước cam loại I và II pha chế được nên x ≥ 0 và y ≥ 0.
Số gam bột cam cần dùng để pha chế x lít nước cam loại I là: 30x (g).
Số gam bột cam cần dùng để pha chế y lít nước cam loại II là: 20y (g).
Số gam bột cam Cúc cần dùng để pha hai loại nước cam là : 30x + 20y (g).
Vì số bột cam Cúc có thể dùng không quá 100 g nên ta có bất phương trình : 30x + 20y ≤ 100 hay 3x + 2y ≤ 10.
Vậy ta có ba bất phương trình mô tả số lít nước cam loại I và II mà bạn Cúc có thể pha chế được là:
x ≥ 0;
y ≥ 0;
3x + 2y – 10 ≤ 0.
Biểu diễn miền nghiệm của ba bất phương trình trên cùng một mặt phẳng tọa độ Oxy ta được:
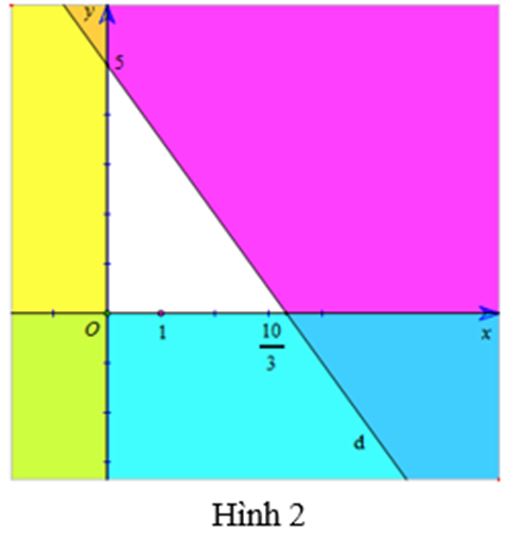
+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bên phải trục Ox, kể cả bờ Ox, (là miền không tô màu vàng trong hình 2).
+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía trên trục Oy, kể cả bờ Oy, (là miền không tô màu xanh trong hình 2).
+ Miền nghiệm của bất phương trình 3x + 2y – 10 ≤ 0 là nửa mặt phẳng kể cả bờ d, chứa điểm O (là miền không tô màu tím trong hình 2).
Bài 5 trang 32 SGK Toán 10 CTST Tập 1
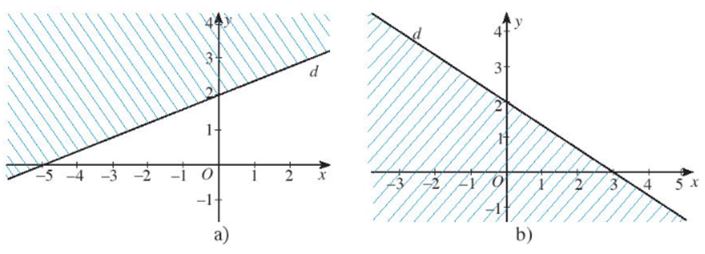
Miền không gạch chéo (không kể bờ d) trong mỗi hình dưới đây là miền nghiệm của bất phương trình nào?
Lời giải
a) Giả sử phương trình đường thẳng d có dạng là y = ax + b
Đường thẳng d đi qua hai điểm (0; 2) và (- 5; 0) nên ta có:
\(\left\{\begin{array}{l}2=a.0+b\\0=a.(-5)+b\end{array}\right.\)
Giải hệ trên ta được a = \(\frac25\), b = 2. Suy ra y = \(\frac25\)x + 2 hay 2x – 5y + 10 = 0.
Vậy ta có phương trình đường thẳng d là 2x – 5y + 10 = 0.
Mặt khác O (0; 0) không thuộc d và thuộc miền nghiệm của bất phương trình.
Mà 2.0 – 5.0 + 10 = 10 > 0.
Hơn nữa miền nghiệm không kể đường thẳng d nên bất phương trình cần tìm là 2x – 5y + 10 > 0.
b) Giả sử phương trình đường thẳng d có dạng là y = ax + b
Đường thẳng d đi qua hai điểm (3; 0) và (0; 2) nên ta có:
\(\left\{\begin{array}{l}0=a.3+b\\2=a.0+b\end{array}\right.\)
Giải hệ trên ta được a = −\(\frac23\) , b = 2. Suy ra y = −\(\frac23\)x + 2 hay 2x + 3y – 6 = 0.
Vậy ta có phương trình đường thẳng d là 2x + 3y – 6 = 0.
Mặt khác O (0; 0) không thuộc d và không thuộc miền nghiệm của bất phương trình.
Mà 2.0 + 3.0 – 6 = – 6 < 0.
Hơn nữa miền nghiệm của bất phương trình không kể đường thẳng d nên bất phương trình cần tìm là 2x + 3y – 6 > 0.
2. Giải Toán 10 bài Bất phương trình bậc nhất hai ẩn CD
Mời bạn đọc cùng tham khảo thêm tại Giải Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn CD
Bài 1 trang 24 SGK Toán 10 CD Tập 1
Cặp số nào sau đây là nghiệm của bất phương trình 2x – 3y < 3?
a) (0; – 1);
b) (2; 1);
c) (3; 1).
Lời giải
Ta có: 2x – 3y < 3 (1).
a) Thay x = 0, y = – 1 vào bất phương trình (1) ta được: 2 . 0 – 3 . (– 1) < 3
⇔ 3 < 3 (vô lí)
Vậy cặp số (0; – 1) không phải là nghiệm của bất phương trình đã cho.
b) Tương tự ta có: 2 . 2 – 3 . 1 = 4 – 3 = 1 < 3 (luôn đúng)
Vậy cặp số (2; 1) là một nghiệm của bất phương trình đã cho.
c) Ta có: 2 . 3 – 3 . 1 = 6 – 3 = 3 < 3 (vô lí).
Vậy cặp số (3; 1) không phải là nghiệm của bất phương trình đã cho.
Bài 2 trang 24 SGK Toán 10 CD Tập 1
Biểu diễn miền nghiệm của mỗi bất phương trình sau:
a) x + 2y < 3;
b) 3x – 4y ≥ – 3;
c) y ≥ – 2x + 4;
d) y < 1 – 2x.
Lời giải
a) x + 2y < 3
+ Vẽ đường thẳng d: x + 2y = 3.
+ Lấy điểm O(0; 0). Ta có: 0 + 2.0 = 0 < 3.
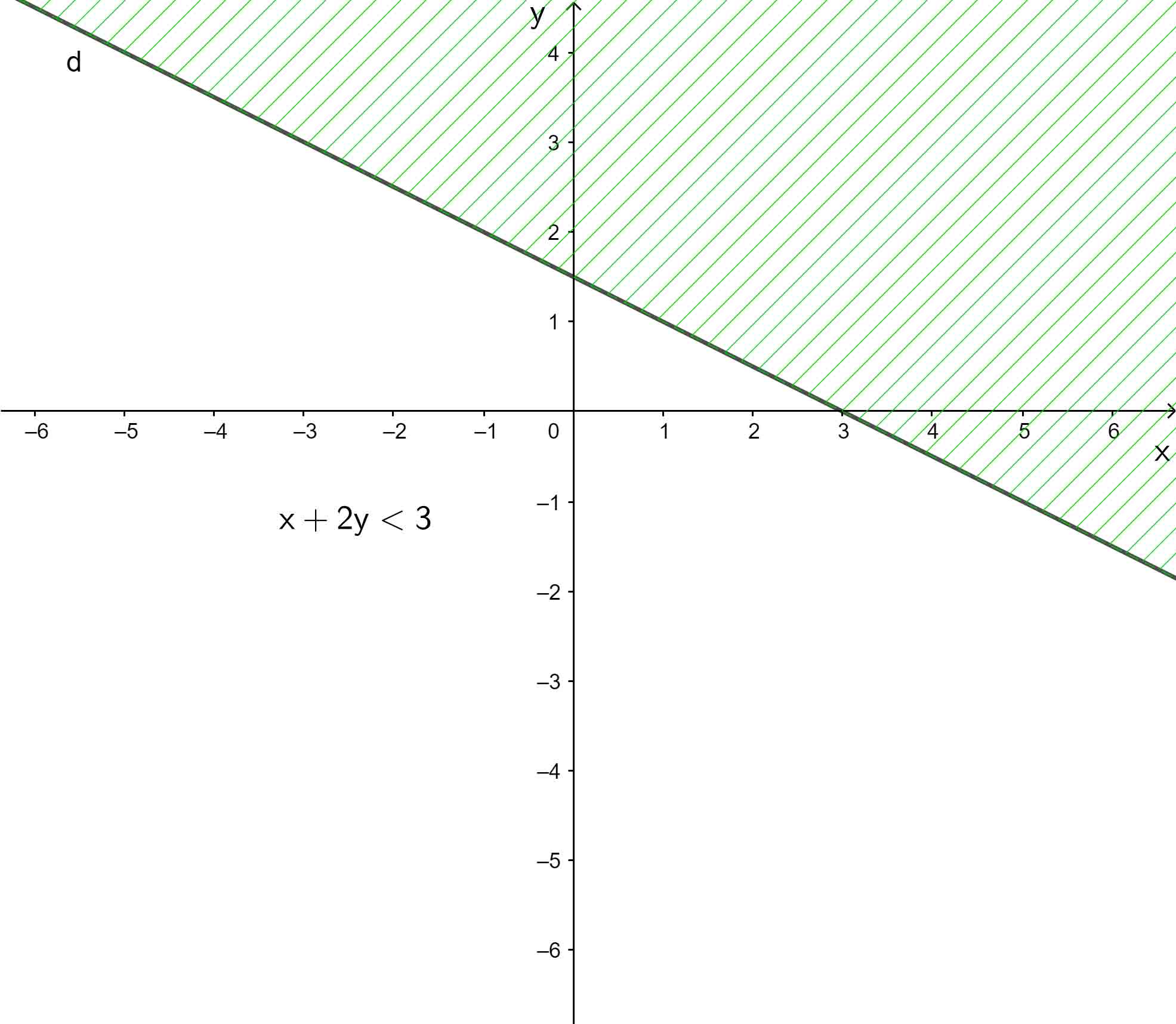
Vậy miền nghiệm của bất phương trình x + 2y < 3 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) không kể đường thẳng d.
b) 3x – 4y ≥ – 3
+ Vẽ đường thẳng d: 3x – 4y = – 3.
+ Lấy điểm O(0; 0). Ta có: 3 . 0 – 4 . 0 = 0 > – 3.
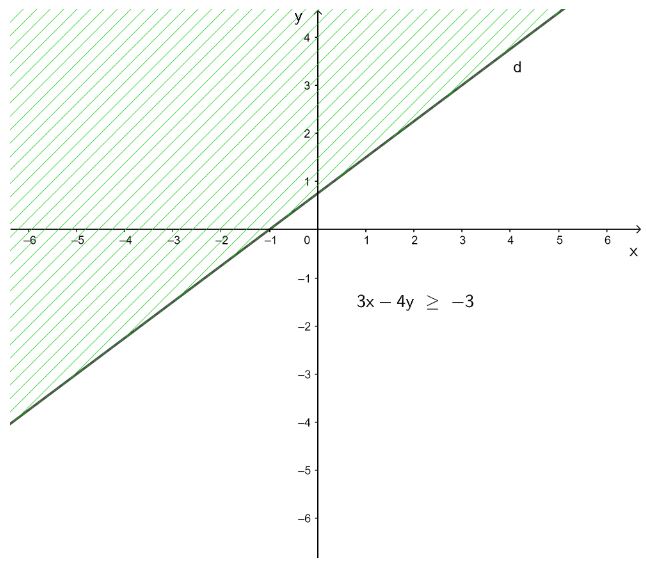
Vậy miền nghiệm của bất phương trình 3x – 4y ≥ – 3 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) kể cả đường thẳng d.
c) y ≥ – 2x + 4
⇔ 2x + y ≥ 4
+ Vẽ đường thẳng d: 2x + y = 4.
+ Lấy điểm O(0; 0). Ta có: 2 . 0 + 0 = 0 < 4.
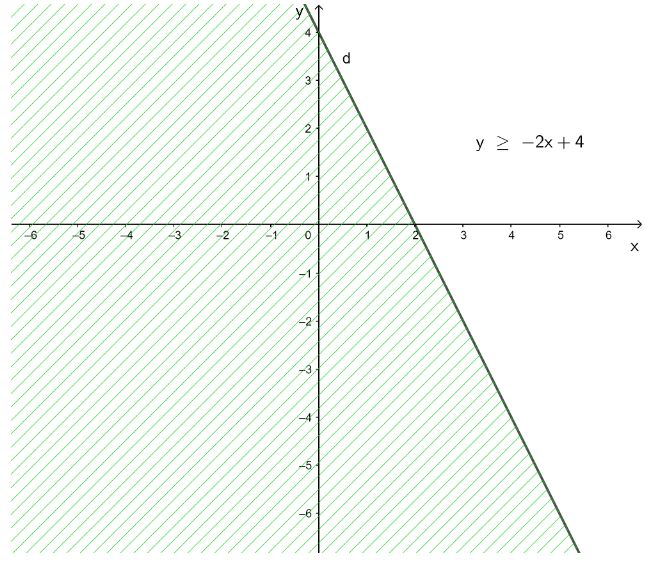
Vậy miền nghiệm của bất phương trình 2x + y ≥ 4 hay chính là y ≥ – 2x + 4 là nửa mặt phẳng không bị gạch ở hình trên không chứa điểm O(0; 0) kể cả đường thẳng d.
d) y < 1 – 2x
⇔ 2x + y < 1
+ Vẽ đường thẳng d: 2x + y = 1.
+ Lấy O(0; 0). Ta có: 2 . 0 + 0 = 0 < 1.
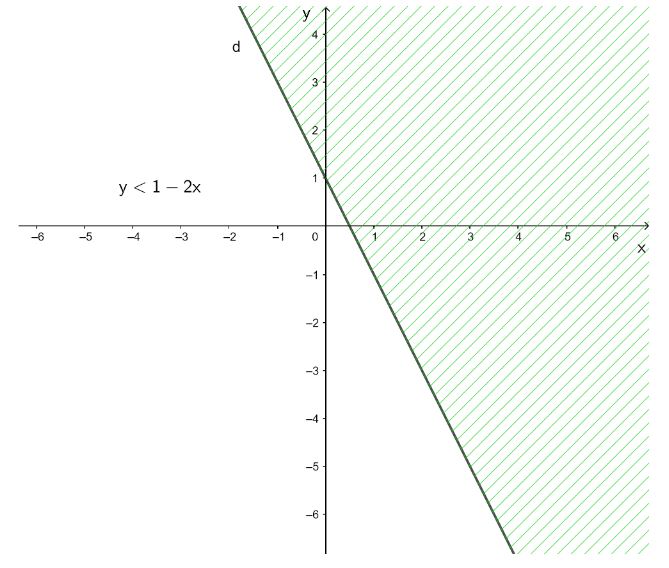
Vậy miền nghiệm của bất phương trình 2x + y < 1 hay chính là y < 1 – 2x là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) không kể đường thẳng d.
Bài 3 trang 24 SGK Toán 10 CD Tập 1
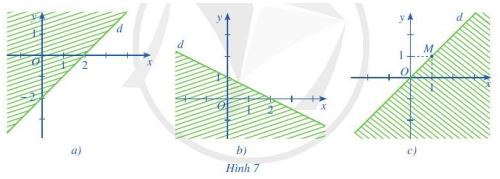
Phần không gạch (không kể d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?
Lời giải
a) Giả sử đường thẳng d: y = ax + b (1) (a ≠ 0)
Quan sát Hình 7a, ta thấy đường thẳng d đi qua hai điểm (0; – 2) và (2; 0).
Thay x = 0, y = – 2 vào (1) ta được: – 2 = b hay b = – 2
Thay x = 2, y = 0 vào (1) ta được: 0 = 2a + b
Suy ra 2a = – b = 2 ⇒ a = 1 (t/m).
Khi đó đường thẳng d: y = x – 2 ⇔ x – y = 2
Xét điểm O(0; 0), ta có: 0 – 0 = 0 < 2
Lại có trên Hình 7a điểm O(0; 0) thuộc phần gạch sọc.
Vậy phần không gạch (không kể d) là miền nghiệm của bất phương trình x – y > 2.
b) Giả sử đường thẳng d: y = ax + b (2) (a ≠ 0)
Quan sát Hình 7b, ta thấy đường thẳng d đi qua 2 điểm (0; 1) và (2; 0).
Thay x = 0, y = 1 vào (2), ta được: b = 1
Thay x = 2, y = 0 vào (2), ta được: 2a + b = 0
Suy ra 2a + 1 = 0 ⇔ a = −\(\frac12\)(t/m)
Khi đó đường thẳng d: y = −\(\frac12\)x+ 1 ⇔ x + 2y = 2
Xét điểm O(0; 0). Ta có: 0 + 0 = 0 < 2.
Lại có trên Hình 7b điểm O(0; 0) thuộc phần gạch sọc.
Vậy phần không gạch sọc (không kể d) là miền nghiệm của bất phương trình x + 2y > 2.
c) Quan sát Hình 7c, ta thấy đường thẳng d đi qua gốc tọa độ và đi qua điểm M(1; 1).
Do đó phương trình đường thẳng d có dạng: y = ax (a ≠ 0)
Vì d đi qua M nên thay x = 1, y = 1 vào y = ax, ta được: a = 1 (t/m)
Do đó đường thẳng d: y = x ⇔ x – y = 0
Xét điểm (1; 0). Ta có: 1 – 0 = 1 > 0.
Lại có trên Hình 7c điểm (1; 0) nằm trên phần gạch sọc.
Vậy phần không gạch sọc (không kể d) là miền nghiệm của bất phương trình x – y < 0.
Bài 4 trang 24 SGK Toán 10 CD Tập 1
Một gian hàng trưng bày bàn và ghế rộng 60 m2. Diện tích để kê một chiếc ghế là 0,5 m2, một chiếc bàn là 1,2 m2. Gọi x là số chiếc ghế, y là số chiếc bàn được kê.
a) Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn và ghế biết diện tích mặt sàn dành cho lưu thông tối thiểu là 12m2.
b) Chỉ ra ba nghiệm của bất phương trình trên.
Lời giải
a) Điều kiện: x ∈ N, y ∈ N
Vì diện tích mặt sàn dành cho lưu thông tối thiểu là 12 m2, do đó diện tích phần mặt sàn để kê bàn và ghế tối đa là: 60 – 12 = 48 (m2).
Diện tích để kê một chiếc ghế là 0,5 m2, nên diện tích để kê x chiếc ghế là 0,5x (m2).
Diện tích để kê một chiếc bàn là 1,2 m2, nên diện tích để kê y chiếc bàn là 1,2y (m2).
Tổng diện tích cho phần mặt sàn để kê x chiếc ghế và y chiếc bàn là: 0,5x + 1,2y (m2).
Do đó, bất phương trình cần tìm là: 0,5x + 1,2y ≤ 48.
b) Cặp số (x0; y0) là nghiệm của bất phương trình 0,5x + 1,2y ≤ 48 nếu 0,5x0 + 1,2y0 ≤ 48. (chú ý x0 và y0 là các số tự nhiên, do đây là số chiếc bàn và ghế)
+ Chọn x0 = 2, y0 = 5, ta có: 0,5 . 2 + 1,2 . 5 = 1 + 6 = 7 < 48.
+ Chọn x0 = 4, y0 = 10, ta có: 0,5 . 4 + 1,2 . 10 = 2 + 12 = 14 < 48.
+ Chọn x0 = 6, y0 = 20, ta có: 0,5 . 6 + 1,2 . 20 = 3 + 24 = 27 < 48.
Vậy ba cặp số (2; 5), (4; 10), (6; 20) là ba nghiệm của bất phương trình 0,5x + 1,2y ≤ 48.
Chú ý: Bất phương trình bậc nhất hai ẩn có vô số nghiệm, nên có thể chọn cặp số tùy ý thỏa mãn.
Bài 5 trang 24 SGK Toán 10 CD Tập 1
Trong 1 lạng (100 g) thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein. Trung bình trong một ngày, một người phụ nữ cần tối thiểu 46 g protein. (Nguồn: https://vinmec.com và https://thanhnien.vn) Gọi x, y lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày và chỉ ra ba nghiệm của bất phương trình đó.
Lời giải
Trong 1 lạng thịt bò chứa khoảng 26 g protein nên trong x lạng thịt bò chứa khoảng 26x (g protein).
Trong 1 lạng cá rô phi chứa khoảng 20 g protein nên trong y lạng cá rô phi chứa khoảng 20y (g protein).
Tổng số lượng protein mà một người phụ nữ nên ăn trong một ngày là: 26x + 20y (g protein).
Trung bình mỗi ngày, một người phụ nữ cần tối thiểu 46 g protein.
Do đó, bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày là: 26x + 20y ≥ 46.
Cặp số (x0; y0) là nghiệm của bất phương trình 26x + 20y ≥ 46 nếu 26x0 + 20y0 ≥ 46.
+ Chọn x0 = 1, y0 = 1, ta có: 26 . 1 + 20 . 1 = 46
+ Chọn x0 = 2, y0 = 1, ta có: 26 . 2 + 20 . 1 = 72 > 46
+ Chọn x0 = 1, y0 = 2, ta có: 26 . 1 + 20 . 2 = 66 > 46
Vậy ba cặp số (1; 1), (2; 1), (1; 2) là ba nghiệm của bất phương trình 26x + 20y ≥ 46.
3. Giải Toán 10 bài Bất phương trình bậc nhất hai ẩn KNTT
Mời bạn đọc tham khảo thêm tại Giải Toán 10 Bài 3 Bất phương trình bậc nhất hai ẩn KNTT
Bài 2.1 trang 25 SGK Toán 10 KNTT Tập 1
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
a) 2x + 3y > 6;
b) 22x + y ≤ 0;
c) 2x2 – y ≥ 1.
Lời giải
Bất phương trình bậc nhất hai ẩn x,y có dạng tổng quát là: ax + by > c (ax + by < c, ax + by ≥ 0, ax + by ≤ 0)
Trong đó a, b, c là số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.
Do đó:
a) 2x + 3y > 6 là bất phương trình bậc nhất hai ẩn với a = 2, b = 3 và c = 6;
b) 22x + y ≤ 0 là bất phương trình bậc nhất hai ẩn với a = 22, b = 1 và c = 0.
Bài 2.2 trang 25 SGK Toán 10 KNTT Tập 1
Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ:
a) 3x + 2y ≥ 300;
b) 7x + 20y < 0.
Lời giải
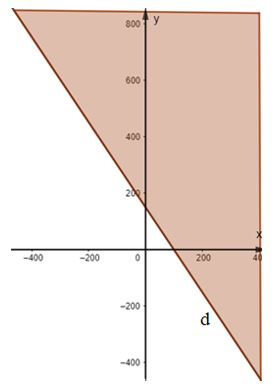
a)
Vẽ đường thẳng d: 3x + 2y – 300 = 0 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 3.0 + 2.0 = 0 < 300.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa gốc tọa độ và cả đường thẳng d (miền tô màu kể cả biên).
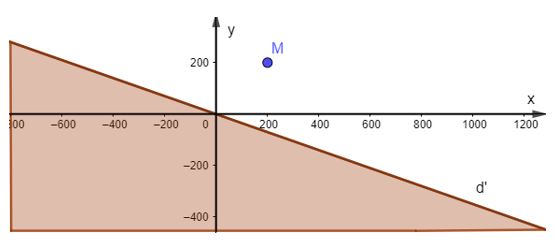
b)
Vẽ đường thẳng d’: 7x + 20y = 0 trên mặt phẳng tọa độ.
Lấy điểm M (200; 200) và tính 7.200 + 20.200 = 5400 > 0.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d’ không chứa điểm M và không chứa đường thẳng d’ (miền tô màu không kể biên).
Bài 2.3 trang 25 SGK Toán 10 KNTT Tập 1
Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:
a) Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng.
b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ.
Lời giải
a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
900.5 + 8x = 4 500 + 8x (nghìn đồng).
Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
1 500.2 + 10y = 3 000 + 10y (nghìn đồng).
Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:
4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).
Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì
7 500 + 8x + 10y ≤ 14 000
⇔ 8x + 10y ≤ 6 500.
⇔ 4x + 5y ≤ 3 250.
Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.
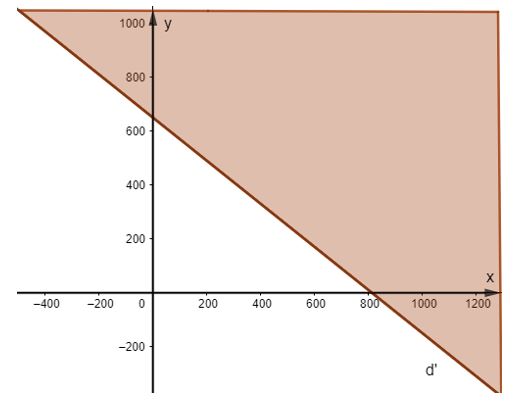
b)
Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d kchứa gốc tọa độ và cả đường thẳng d (miền không tô màu kể cả biên).
Toán 10 Bài 4: Bất phương trình bậc nhất hai ẩn theo chương trình SGK cũ
A. Lý thuyết Bất phương trình bậc nhất hai ẩn
1. Bất phương trình bậc nhất hai ẩn
Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là
\(ax+by\ge c\) (1)
Hoặc \(ax+by \le c,ax+by > c,ax+by < c\)
Trong đó a, b, c là những số thực đã cho, a, b không đồng thời bằng 0, x, y là các ẩn số
Ví dụ: \({{x}^{2}}+2y+1>0,x+2y<0\)
- Biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn
+ Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm bất phương trình (1) được gọi là miền nghiệm
+ Biểu diễn hình học tập nghiệm như sau:
· Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng d: ax + by = c
· Bước 2: Lấy một điểm \(M\left( {{x}_{0}},{{y}_{0}} \right)\) không thuộc d
· Bước 3: Tính \(a{{x}_{0}}+b{{y}_{0}}\) và so sánh với c
· Bước 4: Kết luận:
- Nếu \(a{{x}_{0}}+b{{y}_{0}}< c\) thì nửa mặt phẳng bờ d chứa M là miền nghiệm của \(a{{x}_{0}}+b{{y}_{0}}\le c\)
- Nếu \(a{{x}_{0}}+b{{y}_{0}}>c\) thì nửa mặt phẳng bờ d không chứa M là miền nghiệm của \(a{{x}_{0}}+b{{y}_{0}}\le c\)
2. Hệ bất phương trình bậc nhất hai ẩn
- Định nghĩa: Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn x, y mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho.
- Một trong các ứng dụng quan trọng của hệ bất phương trình bậc nhất nhiều ẩn là bài toán quy hoạch tuyến tính tìm phương án tối ưu.
Bài toán tối ưu: Cho hệ bất phương trình: \(\left\{ \begin{matrix} {{a}_{1}}x+{{b}_{1}}y\le 0 \\ ... \\ {{a}_{k}}x+{{b}_{k}}y\ge 0 \\ \end{matrix} \right.\)(*). Tìm cặp (x, y) thỏa mãn hệ bất phương trình trên đồng thời làm cho biểu thức F = f(x, y) đạt giá trị lớn nhất hoặc nhỏ nhất.
Phương pháp chung
Bước 1: Xác định miền đa giác \({{A}_{1}},{{A}_{2}},...,{{A}_{n}}\) thỏa mãn hệ (*)
Bước 2: Tính các giá trị \({{F}_{1}},{{F}_{2}},{{F}_{3}},...,{{F}_{n}}\) của hàm F tại các đỉnh \({{A}_{1}},{{A}_{2}},...,{{A}_{n}}\)
Bước 3: Ta có:
- \({{F}_{\min }}=\min \left\{ {{F}_{1}},{{F}_{2}},{{F}_{3}},...,{{F}_{n}} \right\}\)
- \({{F}_{\max }}=\max \left\{ {{F}_{1}},{{F}_{2}},{{F}_{3}},...,{{F}_{n}} \right\}\)
B. Giải SGK Toán 10 Bài 4
Trong Sách giáo khoa Toán lớp 10, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 10. Mời các bạn học sinh tham khảo:
C. Giải SBT Toán 10 Bài 4
Sách bài tập Toán 10 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:
D. Bài tập trắc nghiệm Toán 10 Bất phương trình
Để ôn tập lại kiến thức cũng như rèn luyện nâng cao hơn về bài tập của phần Bất phương trình này, VnDoc xin gửi tới các bạn học sinh Tài liệu Bài tập Bất phương trình bậc nhất hai ẩn do VnDoc biên soạn. Qua đó sẽ giúp các bạn học sinh hiểu sâu hơn và nắm rõ hơn lý thuyết cũng như bài tập của bài học này. Mời các bạn học sinh tham khảo:
------------------------------------
Trên đây VnDoc đã giới thiệu tới các bạn tài liệu Bất phương trình bậc nhất hai ẩn. Hy vọng với tài liệu này các bạn học sinh sẽ nắm chắc kiến thức vận dụng tốt vào giải bài tập từ đó học tốt môn Toán lớp 10. Chúc các bạn học tốt và nhớ thường xuyên tương tác để cập nhật được nhiều bài tập hay bổ ích nhé!
Ngoài ra, VnDoc giới thiệu thêm tới bạn đọc tham khảo một vài tài liệu liên quan tới chương trình lớp 10: Ngữ Văn 10, Tiếng Anh lớp 10, Vật lý lớp 10,...
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 10, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 10 sau: Nhóm Tài liệu học tập lớp 10 . Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
