Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

35 bài tập hệ thức lượng trong tam giác có hướng dẫn

Bài tập Toán lớp 10 có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 10

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

35 bài tập hệ thức lượng trong tam giác

Nhắc lại công thức hệ thức lượng trong tam giác
Bài tập hệ thức lượng trong tam giác

Hệ thức lượng trong tam giác là một phần quan trọng của chương trình Toán lớp 10, giúp học sinh nắm vững mối quan hệ giữa các cạnh, góc và đường cao trong tam giác. Nắm chắc kiến thức này sẽ hỗ trợ giải nhanh các bài toán hình học và vận dụng trong nhiều dạng đề thi. Bài viết này tổng hợp 35 bài tập hệ thức lượng trong tam giác kèm hướng dẫn chi tiết, giúp các em vừa rèn kỹ năng vừa củng cố lý thuyết một cách hiệu quả.

Nhắc lại công thức hệ thức lượng trong tam giác

a. Định lí cosin

Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai góc còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.

Ta có hệ thức sau:

$a^2=b^2+c^2-2.b.c.cos\hat{A}$ $a^2=b^2+c^2-2.b.c.cos\hat{A}$

$b^2=a^2+c^2-2.a.c.cos\hat{B}$ $b^2=a^2+c^2-2.a.c.cos\hat{B}$

$c^2=a^2+b^2-2a.b.cos\hat{C}$ $c^2=a^2+b^2-2a.b.cos\hat{C}$

b. Tính độ dài đường trung tuyến của tam giác

Cho tam giác ABC có cạnh AB = c, AC = b, BC = a. Gọi độ dài các đường trung tuyến lần lượt vẽ từ các đỉnh A, B, C của tam giác ABC là: _{$m_a,m_b,m_c$} ta có:

$m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}$ $m_a^2=\frac{b^2+c^2}{2}-\frac{a^2}{4}$

$m^2_b=\dfrac{a^2+c^2}{2}-\dfrac{b^2}{4}$ $m^2_b=\dfrac{a^2+c^2}{2}-\dfrac{b^2}{4}$

$m^2_c=\dfrac{b^2+a^2}{2}-\dfrac{c^2}{4}$ $m^2_c=\dfrac{b^2+a^2}{2}-\dfrac{c^2}{4}$

c. Định lí sin

Trong tam giác ABC bất kì, tỉ số giữa cạnh và sin của góc đối diện với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$ $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$

Với R là bán kính đường tròn ngoại tiếp tam giác

d. Công thức diện tích tam giác

Giả sử $h_a,h_b,h_c$ là các đường cao lần lượt kẻ từ đỉnh A, B, C của tam giác ABC.

Diện tích tam giác ABC được tính theo một trong các công thức sau:

$\begin{align} & S=\frac{1}{2}.{{h}_{a}}.BC=\frac{1}{2}{{h}_{b}}.AC=\frac{1}{2}{{h}_{c}}.AB \\ & S=\frac{1}{2}a.b.\sin \widehat{C}=\frac{1}{2}a.c.\sin \widehat{B}=\frac{1}{2}c.b.\sin \widehat{A} \\ & S=\frac{a.b.c}{4.R} \\ & S=p.r \\ & S=\sqrt{p.\left( p-a \right)\left( p-b \right)\left( p-c \right)} \\ \end{align}$ $\begin{align} & S=\frac{1}{2}.{{h}_{a}}.BC=\frac{1}{2}{{h}_{b}}.AC=\frac{1}{2}{{h}_{c}}.AB \\ & S=\frac{1}{2}a.b.\sin \widehat{C}=\frac{1}{2}a.c.\sin \widehat{B}=\frac{1}{2}c.b.\sin \widehat{A} \\ & S=\frac{a.b.c}{4.R} \\ & S=p.r \\ & S=\sqrt{p.\left( p-a \right)\left( p-b \right)\left( p-c \right)} \\ \end{align}$

Với p là nửa chu vi của tam giác ABC, r là bán kính đường tròn nội tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC

Bài tập hệ thức lượng trong tam giác

Bài 1. Cho ΔABC có AB = 12, BC = 15, AC = 13

a. Tính số đo các góc của ΔABC

b. Tính độ dài các đường trung tuyến của ΔABC

c. Tính diện tích tam giác ABC, bán kính đường tròn nội tiếp, bán kính đường tròn ngoại tiếp tam giác ABC

d. Tính độ dài đường cao nối từ các đỉnh của tam giác ABC

Hướng dẫn giải

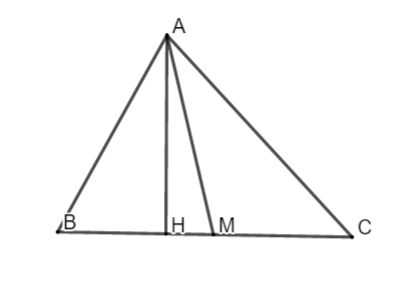
a. Áp dụng hệ thức lượng trong tam giác ta có:

$\begin{align} & A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}-2AC.BC.\cos \widehat{ACB} \\ & \Leftrightarrow {{12}^{2}}={{13}^{2}}+{{15}^{2}}-2.13.15.\cos \widehat{ACB} \\ & \Leftrightarrow \cos \widehat{ACB}=\frac{25}{39}\Rightarrow \widehat{ACB}\approx {{50}^{0}}7$ $\begin{align} & A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}-2AC.BC.\cos \widehat{ACB} \\ & \Leftrightarrow {{12}^{2}}={{13}^{2}}+{{15}^{2}}-2.13.15.\cos \widehat{ACB} \\ & \Leftrightarrow \cos \widehat{ACB}=\frac{25}{39}\Rightarrow \widehat{ACB}\approx {{50}^{0}}7' \\ \end{align}$

$\begin{align} & A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2AB.BC.\cos \widehat{ABC} \\ & \Leftrightarrow {{13}^{2}}={{12}^{2}}+{{15}^{2}}-2.12.15.\cos \widehat{ABC} \\ & \Leftrightarrow \cos \widehat{ABC}=\frac{5}{9}\Rightarrow \widehat{ABC}\approx {{56}^{0}}15$ $\begin{align} & A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2AB.BC.\cos \widehat{ABC} \\ & \Leftrightarrow {{13}^{2}}={{12}^{2}}+{{15}^{2}}-2.12.15.\cos \widehat{ABC} \\ & \Leftrightarrow \cos \widehat{ABC}=\frac{5}{9}\Rightarrow \widehat{ABC}\approx {{56}^{0}}15' \\ \end{align}$

Ta có tổng 3 góc của một tam giác là _{${{360}^{0}}$}

$\Rightarrow \widehat{BAC}=180-{{50}^{0}}7$ $\Rightarrow \widehat{BAC}=180-{{50}^{0}}7'-{{56}^{0}}15'={{73}^{0}}38'$

b. Ta có: _{$A{{M}^{2}}={{m}_{a}}^{2}=\frac{A{{B}^{2}}+A{{C}^{2}}}{2}-\frac{B{{C}^{2}}}{4}=\frac{{{12}^{2}}+{{13}^{3}}}{2}-\frac{{{15}^{2}}}{4}=\frac{401}{4}$}

$\Rightarrow AM=\frac{\sqrt{401}}{2}$ $\Rightarrow AM=\frac{\sqrt{401}}{2}$

Tương tự ta tính được:

$\left\{ \begin{matrix} {{m}_{b}}=\sqrt{\dfrac{A{{B}^{2}}+B{{C}^{2}}}{2}-\dfrac{A{{C}^{2}}}{4}}=\dfrac{\sqrt{569}}{2} \\ {{m}_{c}}=\sqrt{\dfrac{A{{C}^{2}}+B{{C}^{2}}}{2}-\dfrac{A{{B}^{2}}}{4}}=\sqrt{161} \\ \end{matrix} \right.$ $\left\{ \begin{matrix} {{m}_{b}}=\sqrt{\dfrac{A{{B}^{2}}+B{{C}^{2}}}{2}-\dfrac{A{{C}^{2}}}{4}}=\dfrac{\sqrt{569}}{2} \\ {{m}_{c}}=\sqrt{\dfrac{A{{C}^{2}}+B{{C}^{2}}}{2}-\dfrac{A{{B}^{2}}}{4}}=\sqrt{161} \\ \end{matrix} \right.$

c. Để tính được diện tích một cách chính xác nhất ta sẽ áp dụng công thức Hê – rông

- Nửa chu vi tam giác ABC: _{$p=\frac{AB+AC+BC}{2}=\frac{12+13+15}{2}=20$}

- Diện tích tam giác ABC: $S=\sqrt{p\left( p-AB \right)\left( p-AC \right)\left( p-BC \right)}=20\sqrt{14}$ $S=\sqrt{p\left( p-AB \right)\left( p-AC \right)\left( p-BC \right)}=20\sqrt{14}$

- Bán kính đường tròn ngoại tiếp R của tam giác ABC:

${{S}_{ABC}}=\frac{AB.AC.BC}{4.R}\Rightarrow R=\dfrac{AB.AC.BC}{4.{{S}_{ABC}}}=\frac{12.13.15}{4.20\sqrt{14}}=\frac{117\sqrt{14}}{28}$ ${{S}_{ABC}}=\frac{AB.AC.BC}{4.R}\Rightarrow R=\dfrac{AB.AC.BC}{4.{{S}_{ABC}}}=\frac{12.13.15}{4.20\sqrt{14}}=\frac{117\sqrt{14}}{28}$

- Bán kính đường tròn nội tiếp r của tam giác ABC:

${{S}_{ABC}}=p.r\Rightarrow r=\frac{{{S}_{ABC}}}{p}=\frac{20\sqrt{14}}{20}=\sqrt{14}$ ${{S}_{ABC}}=p.r\Rightarrow r=\frac{{{S}_{ABC}}}{p}=\frac{20\sqrt{14}}{20}=\sqrt{14}$

d. Ta có: ${{S}_{ABC}}=\frac{1}{2}{{h}_{a}}.BC=\frac{1}{2}.{{h}_{b}}.AC=\frac{1}{2}.{{h}_{c}}.AB$ ${{S}_{ABC}}=\frac{1}{2}{{h}_{a}}.BC=\frac{1}{2}.{{h}_{b}}.AC=\frac{1}{2}.{{h}_{c}}.AB$

$\Rightarrow \left\{ \begin{matrix}{{h}_{a}}=\dfrac{2.{{S}_{ABC}}}{BC}=\dfrac{2.20\sqrt{14}}{15}=\dfrac{8\sqrt{14}}{3} \\{{h}_{b}}=\dfrac{2.{{S}_{ABC}}}{AC}=\dfrac{2.20\sqrt{14}}{13}=\dfrac{40\sqrt{14}}{13} \\{{h}_{c}}=\dfrac{2.{{S}_{ABC}}}{AB}=\dfrac{2.20\sqrt{14}}{12}=\dfrac{10\sqrt{14}}{3} \\\end{matrix} \right.$ $\Rightarrow \left\{ \begin{matrix}{{h}_{a}}=\dfrac{2.{{S}_{ABC}}}{BC}=\dfrac{2.20\sqrt{14}}{15}=\dfrac{8\sqrt{14}}{3} \\{{h}_{b}}=\dfrac{2.{{S}_{ABC}}}{AC}=\dfrac{2.20\sqrt{14}}{13}=\dfrac{40\sqrt{14}}{13} \\{{h}_{c}}=\dfrac{2.{{S}_{ABC}}}{AB}=\dfrac{2.20\sqrt{14}}{12}=\dfrac{10\sqrt{14}}{3} \\\end{matrix} \right.$

Bài 2. Cho ΔABC có AB = 6, AC = 8, góc A = 120⁰

a. Tính diện tích ΔABC

b. Tính cạnh BC và bán kính đường tròn ngoại tiếp của tam giác ABC

Hướng dẫn giải

a. Diện tích tam giác ABC: ${{S}_{ABC}}=\frac{1}{2}.AB.AC.\sin \widehat{A}=\frac{1}{2}.6.8.\sin {{120}^{0}}=12\sqrt{3}$ ${{S}_{ABC}}=\frac{1}{2}.AB.AC.\sin \widehat{A}=\frac{1}{2}.6.8.\sin {{120}^{0}}=12\sqrt{3}$

b. Ta có:

$\begin{align} & B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2AB.AC.\cos \widehat{A} \\ & \Rightarrow B{{C}^{2}}={{6}^{2}}+{{8}^{2}}-2.6.8.\cos {{120}^{0}}=148 \\ & \Rightarrow BC=2\sqrt{37} \\ \end{align}$ $\begin{align} & B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2AB.AC.\cos \widehat{A} \\ & \Rightarrow B{{C}^{2}}={{6}^{2}}+{{8}^{2}}-2.6.8.\cos {{120}^{0}}=148 \\ & \Rightarrow BC=2\sqrt{37} \\ \end{align}$

- Bán kính đường tròn ngoại tiếp tam giác ABC:

${{S}_{ABC}}=\frac{AB.AC.BC}{4.R}\Rightarrow R=\frac{AB.AC.BC}{4.{{S}_{ABC}}}=\frac{6.8.2\sqrt{37}}{4.12\sqrt{3}}=\frac{2\sqrt{111}}{3}$ ${{S}_{ABC}}=\frac{AB.AC.BC}{4.R}\Rightarrow R=\frac{AB.AC.BC}{4.{{S}_{ABC}}}=\frac{6.8.2\sqrt{37}}{4.12\sqrt{3}}=\frac{2\sqrt{111}}{3}$

Bài 3. Cho ΔABC có a = 8, b = 10, c = 13

a. ΔABC có góc tù hay không?

b. Tính bán kính đường tròn ngoại tiếp ΔABC

c. Tính diện tích ΔABC

HS: Tự giải

Bài 4. Cho ΔABC có góc A = 60⁰, góc B = 45⁰, b = 2. Tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp ΔABC và diện tích tam giác.

HS: Tự giải

Bài 5. Cho ΔABC: AC = 7, AB = 5. Tính BC, S, h_a, R.

HS: Tự giải

Bài 6. Cho ΔABC có m_b = 4, m_c = 2 và a = 3, tính độ dài cạnh AB, AC.

HS: Tự giải

Bài 7. Cho ΔABC có AB = 3, AC = 4 và diện tích S = 3√3. Tính cạnh BC.

HS: Tự giải

Bài 8. Tính bán kính đường tròn nội tiếp ΔABC biết AB = 2, AC = 3, BC = 4

HS: Tự giải

Bài 9. Tính góc A của ΔABC có các cạnh a, b, c thỏa hệ thức b(b² - a²) = c(a² - c²)

HS: Tự giải

Bài 10. Cho ΔABC. Chứng minh rằng:

a. $\frac{\tan A}{\tan B}=\frac{{{c}^{2}}+{{a}^{2}}-{{b}^{2}}}{{{c}^{2}}+{{b}^{2}}-{{a}^{2}}}$ $\frac{\tan A}{\tan B}=\frac{{{c}^{2}}+{{a}^{2}}-{{b}^{2}}}{{{c}^{2}}+{{b}^{2}}-{{a}^{2}}}$

b. ${{c}^{2}}={{\left( a-b \right)}^{2}}+4S.\frac{1-\cos C}{\sin C}$ ${{c}^{2}}={{\left( a-b \right)}^{2}}+4S.\frac{1-\cos C}{\sin C}$

c. $S=2{{R}^{2}}\sin A.\sin B.\sin C$ $S=2{{R}^{2}}\sin A.\sin B.\sin C$

d. $S=\frac{1}{2}\sqrt{{{\overrightarrow{AB}}^{2}}.{{\overrightarrow{AC}}^{2}}-{{\left( \overrightarrow{AB.}\overrightarrow{AC} \right)}^{2}}}$ $S=\frac{1}{2}\sqrt{{{\overrightarrow{AB}}^{2}}.{{\overrightarrow{AC}}^{2}}-{{\left( \overrightarrow{AB.}\overrightarrow{AC} \right)}^{2}}}$

e. $a=b.\cos C+c.\cos B$ $a=b.\cos C+c.\cos B$

f. $\sin A=\frac{2}{bc}\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}$ $\sin A=\frac{2}{bc}\sqrt{p\left( p-a \right)\left( p-b \right)\left( p-c \right)}$

HS: tự giải

Bài 11. Gọi G là trọng tâm tam giác ABC và M là điểm tùy ý. Chứng minh rằng:

a. $M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}=G{{A}^{2}}+G{{B}^{2}}+G{{C}^{2}}+3G{{M}^{2}}$ $M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}=G{{A}^{2}}+G{{B}^{2}}+G{{C}^{2}}+3G{{M}^{2}}$

b. $4\left( {{m}_{a}}^{2}+{{m}_{b}}^{2}+{{m}_{c}}^{2} \right)=3\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)$ $4\left( {{m}_{a}}^{2}+{{m}_{b}}^{2}+{{m}_{c}}^{2} \right)=3\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)$

HS: tự giải

Bài 12. Cho tam giác ABC có b + c = 2a. Chứng minh rằng

a. $\sin B+\sin C=2\sin A$ $\sin B+\sin C=2\sin A$

b. $\frac{2}{{{h}_{a}}}=\frac{1}{{{h}_{b}}}+\frac{1}{{{h}_{c}}}$ $\frac{2}{{{h}_{a}}}=\frac{1}{{{h}_{b}}}+\frac{1}{{{h}_{c}}}$

HS: tự giải

Bài 13. Cho tam giác ABC biết $A\left( 4\sqrt{3},-1 \right);B\left( 0,3 \right);C\left( 8\sqrt{3},3 \right)$ $A\left( 4\sqrt{3},-1 \right);B\left( 0,3 \right);C\left( 8\sqrt{3},3 \right)$

a. Tính các cạnh và các góc còn lại của tam giác ABC.

b. Tính chu vi và diện tích tam giác ABC.

HS: tự giải

Bài 14. Cho tam giác ABC biết $a=40,6;\widehat{B}={{36}^{0}}20$ $a=40,6;\widehat{B}={{36}^{0}}20',\widehat{C}={{73}^{0}}$. Tính $\widehat{A}$ $\widehat{A}$, cạnh b, c của tam giác đó.

HS: tự giải

Bài 15. Cho tam giác ABC biết $a=42,4m;b=36,6m;\widehat{C}={{33}^{0}}10$ $a=42,4m;b=36,6m;\widehat{C}={{33}^{0}}10'$. Tính số đo các góc A, B và độ dài cạnh c.

Bài 16. Để lấp đường dây cao thế từ vị trí A đến vị trí B phải tránh một ngọn núi, do đó người ta phải nối thẳng đường dây từ vị trí A đến vị trí C dài 10km, rồi nối từ vị trí C đến B dài 8km. Biết góc tạo bởi 2 đoạn dây AC và CB là ${{75}^{0}}$ ${{75}^{0}}$. Hỏi so với việc nối thẳng từ A đến B phải tốn thêm bao nhiêu mét dây?

HS: tự giải

Bài 17. 2 Vị trí A và B cách nhau 500m ở bên này bờ sông từ vị trí C ở bên kia bờ sông. Biết $\widehat{CAB}={{87}^{0}},\widehat{CBA}={{62}^{0}}$ $\widehat{CAB}={{87}^{0}},\widehat{CBA}={{62}^{0}}$. Hãy tính khoảng cách AC và BC.

HS: tự giải

Bài 18. Cho tam giác ABC có BC = a, $\widehat{A}=\alpha$ $\widehat{A}=\alpha$ và hai đường trung tuyến BM và CN vuông góc với nhau. Tính diện tích tam giác ABC.

Hướng dẫn giải

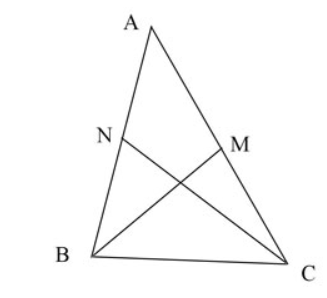
35 bài tập hệ thức lượng trong tam giác có hướng dẫn

Hai đường trung tuyến BM và CN vuông góc với nhau thì ${{\left( \frac{2}{3}{{m}_{b}} \right)}^{2}}+{{\left( \frac{2}{3}{{m}_{c}} \right)}^{2}}={{a}^{2}}$ ${{\left( \frac{2}{3}{{m}_{b}} \right)}^{2}}+{{\left( \frac{2}{3}{{m}_{c}} \right)}^{2}}={{a}^{2}}$

$\begin{align} & \Leftrightarrow \frac{4}{3}\left( \frac{{{a}^{2}}+{{b}^{2}}}{2}-\frac{{{c}^{2}}}{4} \right)+\frac{4}{9}\left( \frac{{{a}^{2}}+{{c}^{2}}}{2}-\frac{{{b}^{2}}}{4} \right)={{a}^{2}} \\ & \Leftrightarrow 5{{a}^{2}}={{b}^{2}}+{{c}^{2}} \\ \end{align}$ $\begin{align} & \Leftrightarrow \frac{4}{3}\left( \frac{{{a}^{2}}+{{b}^{2}}}{2}-\frac{{{c}^{2}}}{4} \right)+\frac{4}{9}\left( \frac{{{a}^{2}}+{{c}^{2}}}{2}-\frac{{{b}^{2}}}{4} \right)={{a}^{2}} \\ & \Leftrightarrow 5{{a}^{2}}={{b}^{2}}+{{c}^{2}} \\ \end{align}$

Mặt khác ${{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc.\cos A$ ${{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc.\cos A$

$\begin{align} & \Leftrightarrow {{a}^{2}}=5{{a}^{2}}-2bc\cos A \\ & \Rightarrow bc=\frac{2{{a}^{2}}}{\cos A}=\frac{2{{a}^{2}}}{\cos \alpha } \\ & \Rightarrow {{S}_{ABC}}=\frac{1}{2}b.c.\sin A={{a}^{2}}\tan \alpha \\ \end{align}$ $\begin{align} & \Leftrightarrow {{a}^{2}}=5{{a}^{2}}-2bc\cos A \\ & \Rightarrow bc=\frac{2{{a}^{2}}}{\cos A}=\frac{2{{a}^{2}}}{\cos \alpha } \\ & \Rightarrow {{S}_{ABC}}=\frac{1}{2}b.c.\sin A={{a}^{2}}\tan \alpha \\ \end{align}$

Bài 19: Cho tam giác ABC. Gọi ${{l}_{a}},{{l}_{b}},{{l}_{c}}$ ${{l}_{a}},{{l}_{b}},{{l}_{c}}$ lần lượt là độ dài các đường phân giác góc A, B, C. Chứng minh rằng:

a. ${{l}_{a}}=\frac{2bc}{b+c}\cos \frac{A}{2}$ ${{l}_{a}}=\frac{2bc}{b+c}\cos \frac{A}{2}$

b. $\frac{\cos \frac{A}{2}}{{{l}_{A}}}+\frac{\cos \frac{B}{2}}{{{l}_{B}}}+\frac{\cos \frac{C}{2}}{{{l}_{C}}}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ $\frac{\cos \frac{A}{2}}{{{l}_{A}}}+\frac{\cos \frac{B}{2}}{{{l}_{B}}}+\frac{\cos \frac{C}{2}}{{{l}_{C}}}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$

c. $\frac{1}{{{l}_{A}}}+\frac{1}{{{l}_{B}}}+\frac{1}{{{l}_{C}}}>\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ $\frac{1}{{{l}_{A}}}+\frac{1}{{{l}_{B}}}+\frac{1}{{{l}_{C}}}>\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$

Hướng dẫn giải

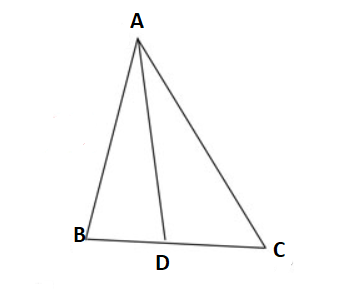
35 bài tập hệ thức lượng trong tam giác có hướng dẫn

Trước hết chứng minh công thức $\sin a=2\sin \frac{a}{2}.\cos \frac{a}{2}$ $\sin a=2\sin \frac{a}{2}.\cos \frac{a}{2}$ bằng cách sử dụng tam giác cân tại đỉnh A có $\widehat{A}=2a$ $\widehat{A}=2a$ thông qua công thức diện tích để đi đến kết luận trên

${{S}_{ABC}}=\frac{1}{2}b.c.\sin A,{{S}_{ABD}}=\frac{1}{2}c.{{l}_{A}}.\sin \frac{A}{2},{{S}_{ACD}}=\frac{1}{2}b.{{l}_{A}}.\sin \frac{A}{2}$ ${{S}_{ABC}}=\frac{1}{2}b.c.\sin A,{{S}_{ABD}}=\frac{1}{2}c.{{l}_{A}}.\sin \frac{A}{2},{{S}_{ACD}}=\frac{1}{2}b.{{l}_{A}}.\sin \frac{A}{2}$

Mà ${{S}_{ABC}}={{S}_{ABD}}+{{S}_{ACD}}\Rightarrow {{l}_{A}}=\frac{2bc}{b+c}.\cos \frac{A}{2}$ ${{S}_{ABC}}={{S}_{ABD}}+{{S}_{ACD}}\Rightarrow {{l}_{A}}=\frac{2bc}{b+c}.\cos \frac{A}{2}$

b. $\frac{\cos \frac{A}{2}}{{{l}_{A}}}=\frac{1}{2}\left( \frac{b+c}{bc} \right)=\frac{1}{2b}+\frac{1}{2c}$ $\frac{\cos \frac{A}{2}}{{{l}_{A}}}=\frac{1}{2}\left( \frac{b+c}{bc} \right)=\frac{1}{2b}+\frac{1}{2c}$

$\begin{align} & \frac{\cos \frac{B}{2}}{{{l}_{B}}}=\frac{1}{2a}+\frac{1}{2c} \\ & \frac{\cos \frac{C}{2}}{{{l}_{C}}}=\frac{1}{2a}+\frac{1}{2b} \\ \end{align}$ $\begin{align} & \frac{\cos \frac{B}{2}}{{{l}_{B}}}=\frac{1}{2a}+\frac{1}{2c} \\ & \frac{\cos \frac{C}{2}}{{{l}_{C}}}=\frac{1}{2a}+\frac{1}{2b} \\ \end{align}$

c. Ta có $\frac{\cos\frac{A}{2}}{l_{A}} + \frac{\cos\frac{B}{2}}{l_{B}} + \frac{\cos\frac{C}{2}}{l_{C}} < \frac{1}{l_{A}} + \frac{1}{l_{B}} + \frac{1}{l_{C}}$ $\frac{\cos\frac{A}{2}}{l_{A}} + \frac{\cos\frac{B}{2}}{l_{B}} + \frac{\cos\frac{C}{2}}{l_{C}} < \frac{1}{l_{A}} + \frac{1}{l_{B}} + \frac{1}{l_{C}}$

$\Rightarrow \frac{1}{l_{A}} + \frac{1}{l_{B}} + \frac{1}{l_{C}} > \frac{1}{a} + \frac{1}{b} + \frac{1}{c}$ $\Rightarrow \frac{1}{l_{A}} + \frac{1}{l_{B}} + \frac{1}{l_{C}} > \frac{1}{a} + \frac{1}{b} + \frac{1}{c}$

Bài 20. Cho tam giác ABC. Gọi $m_{a},m_{b},m_{c}$ $m_{a},m_{b},m_{c}$ lần lượt là độ dài các đường trung tuyến đi qua A, B, C, $m = \frac{m_{a} + m_{b} + m_{c}}{2}$ $m = \frac{m_{a} + m_{b} + m_{c}}{2}$ . Chứng minh rằng

$S_{\Delta ABC} = \frac{3}{4}\sqrt{m\left( m - m_{a} \right)\left( m - m_{b} \right)\left( m - m_{c} \right)}$ $S_{\Delta ABC} = \frac{3}{4}\sqrt{m\left( m - m_{a} \right)\left( m - m_{b} \right)\left( m - m_{c} \right)}$

Hướng dẫn giải:

Hình vẽ minh họa

Gọi D là điểm đối xứng của A qua

trọng tâm G. Ta có tứ giác GBDC là hình bình hành

Dễ thấy $S_{\Delta GBD} = S_{\Delta GBC} = S_{\Delta AGB} = S_{\Delta AGC} = \frac{1}{3}S_{\Delta ABC}$ $S_{\Delta GBD} = S_{\Delta GBC} = S_{\Delta AGB} = S_{\Delta AGC} = \frac{1}{3}S_{\Delta ABC}$

Mà $\Delta GBD$ $\Delta GBD$có ba cạnh $\frac{2}{3}m_{a},\frac{2}{3}m_{b},\frac{2}{3}m_{c}$ $\frac{2}{3}m_{a},\frac{2}{3}m_{b},\frac{2}{3}m_{c}$

$\Rightarrow S_{\Delta GBD} = \left( \frac{2}{3} \right)^{2}\sqrt{m\left( m - m_{a} \right)\left( m - m_{b} \right)\left( m - m_{c} \right)}$ $\Rightarrow S_{\Delta GBD} = \left( \frac{2}{3} \right)^{2}\sqrt{m\left( m - m_{a} \right)\left( m - m_{b} \right)\left( m - m_{c} \right)}$

$\Rightarrow S_{\Delta ABC} = 3S_{\Delta GBD} = \frac{3}{4}\sqrt{m\left( m - m_{a} \right)\left( m - m_{b} \right)\left( m - m_{c} \right)}$ $\Rightarrow S_{\Delta ABC} = 3S_{\Delta GBD} = \frac{3}{4}\sqrt{m\left( m - m_{a} \right)\left( m - m_{b} \right)\left( m - m_{c} \right)}$

Bài 21. Cho tứ giác ABCD nội tiếp trong đường tròn có AB = a, BC = b, CD = c, DA = d. Chứng minh rằng $S_{\square ABCD} = \sqrt{(p - a)(p - b)(p - c)(p - d)}$ $S_{\square ABCD} = \sqrt{(p - a)(p - b)(p - c)(p - d)}$

Với $P = \frac{a + b + c + d}{2}$ $P = \frac{a + b + c + d}{2}$

Hướng dẫn giải:

Hình vẽ minh họa

Do ABCD nội tiếp nên

$\sin\widehat{ABC} = \sin\widehat{ADC}$ $\sin\widehat{ABC} = \sin\widehat{ADC}$

$\cos\widehat{ABC} = - \cos\widehat{ADC}$ $\cos\widehat{ABC} = - \cos\widehat{ADC}$

$S_{ABCD} = S_{ABC} + S_{ADC} = \frac{1}{2}(ab + cd)\sin B$ $S_{ABCD} = S_{ABC} + S_{ADC} = \frac{1}{2}(ab + cd)\sin B$

$= \frac{1}{2}(ab + cd)\sqrt{1 - cos^{2}B}$ $= \frac{1}{2}(ab + cd)\sqrt{1 - cos^{2}B}$

Trong tam giác $ABC$có $AC^{2} = a^{2} + b^{2} - 2ab\cos B$ $AC^{2} = a^{2} + b^{2} - 2ab\cos B$

Trong tam giác $ADC$ có $AC^{2} = c^{2} + d^{2} - 2cd\cos D$ $AC^{2} = c^{2} + d^{2} - 2cd\cos D$

$\Rightarrow a^{2} + b^{2} - 2ab\cos B = c^{2} + d^{2} - 2cdcocD \Leftrightarrow \cos B = \frac{\left( a^{2} + b^{2} \right) - \left( c^{2} + d^{2} \right)}{2(ab + cd)}$ $\Rightarrow a^{2} + b^{2} - 2ab\cos B = c^{2} + d^{2} - 2cdcocD \Leftrightarrow \cos B = \frac{\left( a^{2} + b^{2} \right) - \left( c^{2} + d^{2} \right)}{2(ab + cd)}$

Do đó $S_{ABCD} = \frac{1}{2}(ab + cd)\sqrt{1 - cos^{2}B}$ $S_{ABCD} = \frac{1}{2}(ab + cd)\sqrt{1 - cos^{2}B}$

$= \frac{1}{2}(ab + cd)\sqrt{1 - \left( \frac{\left( a^{2} + b^{2} \right) - \left( c^{2} + d^{2} \right)}{2(ab + cd)} \right)^{2}}$ $= \frac{1}{2}(ab + cd)\sqrt{1 - \left( \frac{\left( a^{2} + b^{2} \right) - \left( c^{2} + d^{2} \right)}{2(ab + cd)} \right)^{2}}$

$= \frac{1}{4}\sqrt{4(ab + cd)^{2} - \left\lbrack \left( a^{2} + b^{2} \right) - \left( c^{2} + d^{2} \right) \right\rbrack^{2}}$ $= \frac{1}{4}\sqrt{4(ab + cd)^{2} - \left\lbrack \left( a^{2} + b^{2} \right) - \left( c^{2} + d^{2} \right) \right\rbrack^{2}}$

$= \frac{1}{4}\sqrt{\left\lbrack (a + b)^{2} - (c - d)^{2} \right\rbrack\left\lbrack (c + d)^{2} - (a - b)^{2} \right\rbrack}$ $= \frac{1}{4}\sqrt{\left\lbrack (a + b)^{2} - (c - d)^{2} \right\rbrack\left\lbrack (c + d)^{2} - (a - b)^{2} \right\rbrack}$

$= \sqrt{\left( \frac{a + b + c - d}{2} \right)\left( \frac{a + b - c + d}{2} \right)\left( \frac{a - b + c + d}{2} \right)\left( \frac{- a + b + c + d}{2} \right)}$ $= \sqrt{\left( \frac{a + b + c - d}{2} \right)\left( \frac{a + b - c + d}{2} \right)\left( \frac{a - b + c + d}{2} \right)\left( \frac{- a + b + c + d}{2} \right)}$

$\Rightarrow S_{\square ABCD} = \sqrt{(p - a)(p - b)(p - c)(p - d)}$ $\Rightarrow S_{\square ABCD} = \sqrt{(p - a)(p - b)(p - c)(p - d)}$Với $p = \frac{a + b + c + d}{2}$ $p = \frac{a + b + c + d}{2}$

Bài 22. Cho tam giác ABC có ba cạnh là a, b, c chứng minh rằng

$\frac{a^{2} + b^{2} + c^{2}}{2abc} = \frac{\cos A}{a} + \frac{\cos B}{b} + \frac{\cos C}{c}$ $\frac{a^{2} + b^{2} + c^{2}}{2abc} = \frac{\cos A}{a} + \frac{\cos B}{b} + \frac{\cos C}{c}$

Hướng dẫn giải:

Ta có $\left( \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} \right)^{2} = 0 \Leftrightarrow AB^{2} + BC^{2} + CA^{2} + 2\overrightarrow{AB}.\overrightarrow{BC} + 2\overrightarrow{BC}.\overrightarrow{CA} + 2\overrightarrow{AB}.\overrightarrow{CA}$ $\left( \overrightarrow{AB} + \overrightarrow{BC} + \overrightarrow{CA} \right)^{2} = 0 \Leftrightarrow AB^{2} + BC^{2} + CA^{2} + 2\overrightarrow{AB}.\overrightarrow{BC} + 2\overrightarrow{BC}.\overrightarrow{CA} + 2\overrightarrow{AB}.\overrightarrow{CA}$

$\Leftrightarrow a^{2} + b^{2} + c^{2} = 2ac\cos B + 2bc\cos A + 2ab\cos C$ $\Leftrightarrow a^{2} + b^{2} + c^{2} = 2ac\cos B + 2bc\cos A + 2ab\cos C$

$\Leftrightarrow \frac{a^{2} + b^{2} + c^{2}}{2abc} = \frac{\cos A}{a} + \frac{\cos B}{b} + \frac{\cos C}{c}$ $\Leftrightarrow \frac{a^{2} + b^{2} + c^{2}}{2abc} = \frac{\cos A}{a} + \frac{\cos B}{b} + \frac{\cos C}{c}$

Bài 23. Cho tam giác ABC có ba cạnh là a, b, c là $a = x^{2} + x + 1,b = 2x + 1,c = x^{2} - 1$ $a = x^{2} + x + 1,b = 2x + 1,c = x^{2} - 1$ chứng minh rằng tam giác có một góc bằng $120^{0}$ $120^{0}$.

Hướng dẫn giải:

Điều kiện a, b, c là 3 cạnh của tam giác $\left\{ \begin{matrix} x^{2} - 1 > 0 \\ 2x + 1 > 0 \\ x^{2} - 1 + 2x + 1 > x^{2} + x + 1 \\ \end{matrix} \right.\ \Leftrightarrow x > 1$ $\left\{ \begin{matrix} x^{2} - 1 > 0 \\ 2x + 1 > 0 \\ x^{2} - 1 + 2x + 1 > x^{2} + x + 1 \\ \end{matrix} \right.\ \Leftrightarrow x > 1$

Với $x > 1$ thì a > b và a > c nên a là cạnh lớn nhất

Tính $\cos A = - \frac{1}{2} \Rightarrow \widehat{A} = 120^{0}$ $\cos A = - \frac{1}{2} \Rightarrow \widehat{A} = 120^{0}$.

Bài 24. Chứng minh rằng với mọi tam giác ABC ta có

a. $\cot A + \cot B + \cot C = \frac{a^{2} + b^{2} + c^{2}}{abc}R$ $\cot A + \cot B + \cot C = \frac{a^{2} + b^{2} + c^{2}}{abc}R$

b. $\sin\frac{A}{2} = \sqrt{\frac{(p - b)(p - c)}{bc}}$ $\sin\frac{A}{2} = \sqrt{\frac{(p - b)(p - c)}{bc}}$

Hướng dẫn giải:

Hình vẽ minh họa

a. Sử dụng định lí sin và cosin.

b. Gọi O là tâm đường tròn nội tiếp

Ta có $S_{\Delta ABC} = pr = \frac{1}{2}bc\sin A\ = bc\sin\frac{A}{2}.cos\frac{A}{2}\ \ \ (1)$ $S_{\Delta ABC} = pr = \frac{1}{2}bc\sin A\ = bc\sin\frac{A}{2}.cos\frac{A}{2}\ \ \ (1)$

Từ hình vẽ:

$r = (p - a)tan\frac{A}{2} \Rightarrow \frac{S_{\Delta ABC}}{p} = (p - a)tan\frac{A}{2}\ \ \ \ \ (2)$ $r = (p - a)tan\frac{A}{2} \Rightarrow \frac{S_{\Delta ABC}}{p} = (p - a)tan\frac{A}{2}\ \ \ \ \ (2)$

Từ (1) và (2) $\frac{\left( S_{\Delta ABC} \right)^{2}}{p} = (p - a)tan\frac{A}{2}bc\sin\frac{A}{2}.cos\frac{A}{2}$ $\frac{\left( S_{\Delta ABC} \right)^{2}}{p} = (p - a)tan\frac{A}{2}bc\sin\frac{A}{2}.cos\frac{A}{2}$

$\Leftrightarrow \frac{p(p - a)(p - b)(p - c)}{p} = bc(p - a)sin\frac{A}{2}$ $\Leftrightarrow \frac{p(p - a)(p - b)(p - c)}{p} = bc(p - a)sin\frac{A}{2}$

$\Rightarrow \sin\frac{A}{2} = \sqrt{\frac{(p - b)(p - c)}{bc}}$ $\Rightarrow \sin\frac{A}{2} = \sqrt{\frac{(p - b)(p - c)}{bc}}$

Bài 25. Tam giác ABC có tính chất gì khi $S_{\Delta ABC} = \frac{1}{4}(a + b - c)(a + c - b)$ $S_{\Delta ABC} = \frac{1}{4}(a + b - c)(a + c - b)$

Hướng dẫn giải:

Theo Hê rong $S_{\Delta ABC} = \sqrt{\left( \frac{a + b + c}{2} \right)\left( \frac{a + b - c}{2} \right)\left( \frac{a - b + c}{2} \right)\left( \frac{- a + b + c}{2} \right)}$ $S_{\Delta ABC} = \sqrt{\left( \frac{a + b + c}{2} \right)\left( \frac{a + b - c}{2} \right)\left( \frac{a - b + c}{2} \right)\left( \frac{- a + b + c}{2} \right)}$

$\Rightarrow (a + b - c)^{2}(a + c - b)^{2}$ $\Rightarrow (a + b - c)^{2}(a + c - b)^{2}$ $= (a + b + c)(a + b - c)(a - b + c)( - a + b + c)$

$\Rightarrow (a + b - c)(a + c - b) = (a + b + c)( - a + b + c) \Leftrightarrow b^{2} + c^{2} = a^{2}$ $\Rightarrow (a + b - c)(a + c - b) = (a + b + c)( - a + b + c) \Leftrightarrow b^{2} + c^{2} = a^{2}$

Suy ra tam giác ABC vuông tại A

Bài 26 Cho tam giác ABC. Gọi R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác. Chứng minh rằng: $\frac{r}{R} \leq \frac{1}{2}$ $\frac{r}{R} \leq \frac{1}{2}$

Hướng dẫn giải:

$r = \frac{S}{p},R = \frac{abc}{4S} \Rightarrow \frac{r}{R} = \frac{S^{2}}{pabc}$ $r = \frac{S}{p},R = \frac{abc}{4S} \Rightarrow \frac{r}{R} = \frac{S^{2}}{pabc}$

$= \frac{4p(p - a)(p - b)(p - c)}{pabc}$ $= \frac{4p(p - a)(p - b)(p - c)}{pabc}$ $= \frac{4(p - a)(p - b)(p - c)}{abc}$ $= \frac{4(p - a)(p - b)(p - c)}{abc}$

Mà $\sqrt{(p - a)(p - b)} \leq \frac{2p - a - b}{2} = \frac{c}{2}$ $\sqrt{(p - a)(p - b)} \leq \frac{2p - a - b}{2} = \frac{c}{2}$

$\sqrt{(p - a)(p - c)} \leq \frac{2p - a - c}{2} = \frac{b}{2}$ $\sqrt{(p - a)(p - c)} \leq \frac{2p - a - c}{2} = \frac{b}{2}$
35 bài tập hệ thức lượng trong tam giác có hướng dẫn

Bài 33. Cho tam giác ABC có sin²B + sin²C = 2sin²A. Chứng minh rằng: A ≤60⁰.

Hướng dẫn giải

Ta có:

sin²B + sin²C = 2sin²A ⇔ b²+ c² = 2a²

Khi đó:

$\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{b^2} + {c^2} - \frac{{{b^2} + {c^2}}}{2}}}{{2bc}}$ $\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{b^2} + {c^2} - \frac{{{b^2} + {c^2}}}{2}}}{{2bc}}$ $= \frac{{{b^2} + {c^2}}}{{4bc}} \geqslant \frac{1}{2} = \cos {60^0}$ $= \frac{{{b^2} + {c^2}}}{{4bc}} \geqslant \frac{1}{2} = \cos {60^0}$.

Bài 34. Cho tam giác ABC có ${a^{\frac{4}{3}}} + {b^{\frac{4}{3}}} = {c^{\frac{4}{3}}}$ ${a^{\frac{4}{3}}} + {b^{\frac{4}{3}}} = {c^{\frac{4}{3}}}$. Chứng minh rằng có một góc tù.

Hướng dẫn giải

Ta có: ${a^{\frac{4}{3}}} + {b^{\frac{4}{3}}} = {c^{\frac{4}{3}}}$ ${a^{\frac{4}{3}}} + {b^{\frac{4}{3}}} = {c^{\frac{4}{3}}}$

$\Leftrightarrow {c^4} = {\left( {{a^{\frac{4}{3}}} + {b^{\frac{4}{3}}}} \right)^3}$ $\Leftrightarrow {c^4} = {\left( {{a^{\frac{4}{3}}} + {b^{\frac{4}{3}}}} \right)^3}$ $= {a^4} + {b^4} + 3{a^{\frac{4}{3}}}.{b^{\frac{4}{3}}}\left( {{a^{\frac{4}{3}}} + {b^{\frac{4}{3}}}} \right)$ $= {a^4} + {b^4} + 3{a^{\frac{4}{3}}}.{b^{\frac{4}{3}}}\left( {{a^{\frac{4}{3}}} + {b^{\frac{4}{3}}}} \right)$

$\geqslant {a^4} + {b^4} + {a^{\frac{4}{3}}}.{b^{\frac{4}{3}}}\left( {{a^{\frac{4}{3}}} + {b^{\frac{4}{3}}}} \right)$ $\geqslant {a^4} + {b^4} + {a^{\frac{4}{3}}}.{b^{\frac{4}{3}}}\left( {{a^{\frac{4}{3}}} + {b^{\frac{4}{3}}}} \right)$ $\geqslant {a^4} + {b^4} + 2{a^{\frac{4}{3}}}.{b^{\frac{4}{3}}}.{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}$ $\geqslant {a^4} + {b^4} + 2{a^{\frac{4}{3}}}.{b^{\frac{4}{3}}}.{a^{\frac{2}{3}}} + {b^{\frac{2}{3}}}$

$= {a^4} + {b^4} + 2{a^2}{b^2} = {\left( {{a^2} + {b^2}} \right)^2}$ $= {a^4} + {b^4} + 2{a^2}{b^2} = {\left( {{a^2} + {b^2}} \right)^2}$

$\Rightarrow {c^2} > {a^2} + {b^2}$ $\Rightarrow {c^2} > {a^2} + {b^2}$

Mà $\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} < 0 \Rightarrow C \geqslant {90^0}$ $\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} < 0 \Rightarrow C \geqslant {90^0}$.

Bài 35. Tam giác ABC có a² + b² + c² = 36r² thì có tính chất gì?

Hướng dẫn giải

Ta có:

${a^2} + {b^2} + {c^2} = \frac{{36.{S^2}}}{{{p^2}}} = 36.\frac{{\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}}{p}$ ${a^2} + {b^2} + {c^2} = \frac{{36.{S^2}}}{{{p^2}}} = 36.\frac{{\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}}{p}$

$= 36\frac{{\sqrt {\left( {p - b} \right)\left( {p - c} \right)} .\sqrt {\left( {p - a} \right)\left( {p - c} \right)} .\sqrt {\left( {p - a} \right)\left( {p - b} \right)} }}{p}$ $= 36\frac{{\sqrt {\left( {p - b} \right)\left( {p - c} \right)} .\sqrt {\left( {p - a} \right)\left( {p - c} \right)} .\sqrt {\left( {p - a} \right)\left( {p - b} \right)} }}{p}$

Ta có:

$2\sqrt {\left( {p - b} \right)\left( {p - c} \right)} \leqslant \left( {2p - b + 2p - c} \right) = a$ $2\sqrt {\left( {p - b} \right)\left( {p - c} \right)} \leqslant \left( {2p - b + 2p - c} \right) = a$

Suy ra $\frac{{\sqrt {\left( {p - b} \right)\left( {p - c} \right)} .\sqrt {\left( {p - a} \right)\left( {p - c} \right)} .\sqrt {\left( {p - a} \right)\left( {p - b} \right)} }}{p} \leqslant \frac{{abc}}{{8p}}$ $\frac{{\sqrt {\left( {p - b} \right)\left( {p - c} \right)} .\sqrt {\left( {p - a} \right)\left( {p - c} \right)} .\sqrt {\left( {p - a} \right)\left( {p - b} \right)} }}{p} \leqslant \frac{{abc}}{{8p}}$

$\Rightarrow {a^2} + {b^2} + {c^2} \leqslant \frac{{9abc}}{{a + b + c}}$ $\Rightarrow {a^2} + {b^2} + {c^2} \leqslant \frac{{9abc}}{{a + b + c}}$ $\Leftrightarrow \left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2}} \right) \leqslant 9abc$ $\Leftrightarrow \left( {a + b + c} \right)\left( {{a^2} + {b^2} + {c^2}} \right) \leqslant 9abc$

Mà ${a^2} + {b^2} + {c^2} \geqslant ab + bc + ca$ ${a^2} + {b^2} + {c^2} \geqslant ab + bc + ca$

$\Rightarrow \left( {a + b + c} \right)\left( {ab + bc + ca} \right) \leqslant 9abc$ $\Rightarrow \left( {a + b + c} \right)\left( {ab + bc + ca} \right) \leqslant 9abc$

$\Leftrightarrow a{\left( {b - c} \right)^2} + b{\left( {c - a} \right)^2} + c{\left( {a - b} \right)^2} \leqslant 0$ $\Leftrightarrow a{\left( {b - c} \right)^2} + b{\left( {c - a} \right)^2} + c{\left( {a - b} \right)^2} \leqslant 0$

$\Leftrightarrow a = b = c$ $\Leftrightarrow a = b = c$

Vậy tam giác ABC có a² + b² + c² = 36r² thì tam giác đó là tam giác đều.

----------------------------------------------------

Việc luyện tập thường xuyên với bài tập hệ thức lượng trong tam giác sẽ giúp học sinh thành thạo kỹ năng tính toán, tăng tốc độ làm bài và hạn chế sai sót. Bộ 35 bài tập có hướng dẫn này sẽ là tài liệu hữu ích để ôn luyện, chuẩn bị tốt cho các bài kiểm tra, thi học kỳ và các kỳ thi quan trọng. Hãy kết hợp học lý thuyết với làm bài tập thường xuyên để đạt kết quả cao nhất.

Tải về

Chọn file muốn tải về: