Giải bất phương trình chứa dấu giá trị tuyệt đối
Bất phương trình chứa dấu giá trị tuyệt đối - Có đáp án
Bạn đang tìm hiểu cách giải bất phương trình chứa dấu giá trị tuyệt đối trong chương trình Toán 10? Đây là dạng toán rất hay gặp trong các đề kiểm tra, thi giữa kỳ và cuối kỳ, yêu cầu học sinh nắm chắc khái niệm giá trị tuyệt đối, biết tách trường hợp và xét dấu hợp lý. Bài viết “Giải bất phương trình chứa dấu giá trị tuyệt đối” dưới đây sẽ hướng dẫn bạn chi tiết từng bước giải, đồng thời cung cấp nhiều bài tập chuyên đề Toán 10 bất phương trình có đáp án để bạn luyện tập và củng cố kiến thức vững chắc.
A. Cách giải bất phương trình chứa dấu giá trị tuyệt đối
Một số kết quả quan trọng thường sử dụng:
1. 
\(\left| f(x) \right| = \left\{
\begin{matrix}
f(x);f(x) \geq 0 \\
- f(x);f(x) < 0 \\
\end{matrix} \right.\)
2. \(\left| f(x) \right|^{2} =
f^{2}(x)\).
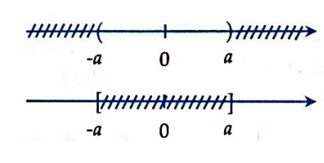
3. Với \(a > 0\) thì:
+ \(\left| f(x) \right| < a
\Leftrightarrow - a < f(x) < a\);
+ \(\left| f(x) \right| > a
\Leftrightarrow \left\lbrack \begin{matrix}
f(x) > a \\
f(x) < - a \\
\end{matrix} \right.\);
4. Cho \(f(x)\) và \(g(x)\) là các biểu thức của x:
- \(\left| f(x) \right| < \left| g(x)
\right| \Leftrightarrow f^{2}(x) < g^{2}(x) \Leftrightarrow
\left\lbrack f(x) - g(x) \right\rbrack.\left\lbrack f(x) + g(x)
\right\rbrack < 0\)
- \(\left| f(x) \right| < \left| g(x)
\right| \Leftrightarrow - g(x) < f(x) < g(x)\)
- \(\left| f(x) \right| > \left| g(x)
\right| \Leftrightarrow \left\lbrack \begin{matrix}
f(x) > g(x) \\
f(x) < - g(x) \\
\end{matrix} \right.\).
B. Bài tập giải bất phương trình chứa dấu giá trị tuyệt đối
Ví dụ 1: Biết tập nghiệm của bất phương trình \(|2x - 1| \leq x + 2\) là đoạn \(\lbrack a;b\rbrack\). Tính \(\lbrack a;b\rbrack\).
A. \(\frac{4}{3}\) B. \(\frac{8}{3}\) C. 4 D. \(\frac{10}{3}\)
Lời giải
Ta có:
\(|2x - 1| \leq x + 2 \Leftrightarrow - (x
+ 2) \leq 2x - 1 \leq x + 2\)
\(\Leftrightarrow \left\{ \begin{matrix}
x \leq 3 \\
3x \geq - 1 \\
\end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix}
x \leq 3 \\
x \geq - \frac{1}{3} \\
\end{matrix} \right.\ \Leftrightarrow - \frac{1}{3} \leq x \leq
3\)
Vậy \(a = - \frac{1}{3};b = 3 \Rightarrow b
- a = 3 - \left( - \frac{1}{3} \right) = \frac{10}{3}\).
Đáp án D.
Ví dụ 2: Có bao nhiêu số tự nhiên khác 0 thuộc tập nghiệm của bất phương trình: \(\frac{\left| x^{2} - 4x
\right| + 3}{x^{2} + |x - 5|} \geq 1\) (1)?
A. 0 B. 2 C. 5 D. Vô số
Lời giải
Lập bảng chia khoảng xét dấu hai biểu thức \(x^{2} - 4x\) và \(x - 5\):
- TH1: Với \(x \leq 0\) hoặc \(4 < x \leq 5\), bất phương trình (1) trở thành:
\(\frac{x^{2} - 4x + 3}{x^{2} + x - 5} \geq1\)\(\Leftrightarrow x^{2} - 4x + 3 \geq x^{2} + x - 5\) (do \(x^{2} + x - 5 > 0;\forall x\))
\(\Leftrightarrow 3x \leq - 2
\Leftrightarrow x \leq - \frac{2}{3}\).
Vậy trong trường hợp này bất phương trình đã cho có nghiệm là \(x \in \left( - \infty; - \frac{2}{3}
\right\rbrack\).
- TH2: Với \(0 < x \leq 4\), bất phương trình (1) trở thành:
\(\frac{- x^{2} + 4x + 3}{x^{2} - x + 5}
\geq 1\)
\(\Leftrightarrow - x^{2} + 4x + 3 \geq
x^{2} - x + 5\)
\(\Leftrightarrow 2x^{2} - 5x + 2 \leq 0
\Leftrightarrow \frac{1}{2} \leq x \leq 2\)
Vậy trong trường hợp này bất phương trình đã cho có nghiệm là \(x \in \left\lbrack \frac{1}{2};2
\right\rbrack\).
- TH3: Với \(x > 5\), bất phương trình (1) trở thành:
\(\frac{x^{2} - 4x + 3}{x^{2} + x - 5} \geq1\)\(\Leftrightarrow x^{2} - 4x + 3 \geq x^{2} + x - 5\) (do với \(x > 5\) thì \(x^{2} + x - 5 > 0\))
\(\Leftrightarrow 5x \leq 8
\Leftrightarrow x \leq \frac{8}{5}(L)\)
Vậy bất phương trình đã cho có nghiệm là \(x \in \left( - \infty; - \frac{2}{3} \right) \cup
\left\lbrack \frac{1}{2};2 \right\rbrack\).
Do đó 2 số tự nhiên khác 0 thuộc tập nghiệm của bất phương trình đã cho.
Đáp án B.
--------------------------------------------------------------
Với những hướng dẫn cụ thể trong bài viết này, bạn đã nắm rõ cách giải bất phương trình chứa dấu giá trị tuyệt đối thông qua phương pháp tách trường hợp, xét dấu và biến đổi tương đương. Khi luyện tập thường xuyên với các bài tập chuyên đề Toán 10 bất phương trình có đáp án, bạn sẽ nhanh chóng thành thạo kỹ năng, tự tin giải nhanh – giải đúng trong mọi kỳ kiểm tra hoặc kỳ thi quan trọng.
Hãy lưu lại bài viết này để ôn tập bất cứ lúc nào, chia sẻ cho bạn bè cùng học và tham khảo thêm nhiều chuyên đề Toán 10 khác như bất phương trình chứa ẩn ở mẫu, bất phương trình tích hay xét dấu tam thức bậc hai. Chúc bạn học tốt và chinh phục mọi bài toán khó một cách dễ dàng!
