Toán 10 Bài 2: Tập hợp

Toán 10 Bài 2: Tập hợp được VnDoc biên soạn bao gồm hướng dẫn lý thuyết và hướng dẫn giải cho từng bài tập sách giáo khoa và sách bài tập giúp các bạn học sinh luyện tập và hiểu rõ hơn thế nào là tập hợp, cách xác định tập hợp, các phép toán trên tập hợp. Qua đó giúp các bạn học sinh ôn tập, củng cố và rèn luyện thêm kiến thức đã học trong chương trình Toán 10, Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết bài viết dưới đây nhé.

A. Lí thuyết Tập hợp

I. Khái niệm tập hợp

1. Tập hợp và phần tử

Ví dụ: Dùng kí hiệu _{\(\in ,\notin\)} để viết các mệnh đề sau:

a. 4 là số tự nhiên

b. _\(\sqrt{3}\) không là số hữu tỉ.

Hướng dẫn

a. _{\(4\in \mathbb{N}\)}

b. _{\(\sqrt{3}\notin \mathbb{Q}\)}

- Tập hợp là khái niệm cơ bản của toán học, không có định nghĩa.

- Để nói a là một phần tử của tập hợp A, ta viết _{\(a\in A\)}, ngược lại _{\(a\notin A\)} để nói a không thuộc A

-Một tập hợp có thể được cho bằng cách liệt kê các phần tử của nó hoặc được cho bằng cách nêu tính chất đặc trưng của các phần tử của nó.

- Một phần tử không có phần tử nào được gọi là tập hợp rỗng, kí hiệu: _{\(\varnothing\)}

2. Cách xác định tập hợp

Ta có thể xác định một tập hợp bằng 2 cách:

a. Liệt kê các phần tử của nó.

b. Chỉ ra tính chất đặc trưng cho các phần tử của nó.

Ví dụ: Cho tập hợp B là các nghiệm của phương trình _{\({{x}^{2}}+3x+2=0\)} được viết là

_{\(B:\left\{ x\in \mathbb{R}:{{x}^{2}}+3x+2=0 \right\}\)} Hãy liệt kê các phần tử có trong tập hợp.

Hướng dẫn

Các phần tử có trong tập hợp _{\(B=\left\{ -1,-2 \right\}\)}

II. Tập hợp con

Ta gọi A là tập hợp con của B, kí hiệu _{\(A\subset B\Leftrightarrow x\in A\Rightarrow x\in B\)}

Ví dụ:

III. Tập hợp bằng nhau

Khi _{\(A\subset B\)} và _{\(B\subset A\)} ta nói tập hợp A bằng tập hợp B và viết là _\(A=B\). Như vậy:

\(A=B\Leftrightarrow \forall x:x\in A\Leftrightarrow x\in B\)

B. Giải SGK Toán 10 Bài 2

Trong Sách giáo khoa Toán lớp 10, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 10. Mời các bạn học sinh tham khảo:

Giải Toán 10 Bài 2: Tập hợp. Các phép toán trên tập hợp Cánh diều

Bài 1 trang 18 SGK Toán 10 Cánh diều Tập 1

Cho tập hợp X = {a; b; c}. Viết tất cả các tập con của tập hợp X.

Lời giải

Các tập hợp con của tập hợp X = {a; b; c} là:

X, {a}, {b}, {c}, {a; b}, {a; c}, {b; c}.

Bài 2 trang 18 SGK Toán 10 Cánh diều Tập 1

Sắp xếp các tập hợp sau theo quan hệ “⊂”: [2; 5], (2; 5), [2; 5), (1; 5]

Lời giải

Tập hợp [2; 5] là tập hợp gồm các số thực lớn hơn hoặc bằng 2 và nhỏ hơn hoặc bằng 5.

Tập hợp (2; 5) là tập hợp gồm các số thực lớn hơn 2 và nhỏ hơn 5.

Tập hợp [2; 5) là tập hợp gồm các số thực lớn hơn hoặc bằng 2 và nhỏ hơn 5.

Tập hợp (1; 5] là tập hợp các số thực lớn hơn 1 và nhỏ hơn hoặc bằng 5.

Do đó ta sắp xếp các tập hợp như sau:

(2; 5) ⊂ [2; 5) ⊂ [2; 5] ⊂ (1; 5].

Bài 3 trang 18 SGK Toán 10 Cánh diều Tập 1

Xác định các tập hợp sau và biểu diễn chúng trên trục số:

a) [– 3; 7] ∩ (2; 5);

b) (– ∞; 0] ∪ (– 1; 2);

c) R\ (– ∞; 3);

Lời giải

a) Do (2; 5) ⊂ [–3 ; 7] nên giao của hai tập hợp [–3; 7] và (2; 5) là khoảng (2; 5)

Vậy [– 3; 7] ∩ (2; 5) = (2; 5) và được biểu diễn là:

b) Ta có: (– ∞; 0] = {x ∈ R| x ≤ 0}

(–1 ; 2) = {x ∈ R| –1 < x < 2}

Khi đó (– ∞; 0] ∪ (–1 ; 2) = {x ∈ R| x ≤ 0 hoặc – 1 < x < 2} = {x ∈ R| x < 2} = (– ∞; 2)

Vậy (– ∞; 0] ∪ (– 1; 2) = (– ∞; 2) và được biểu diễn là:

c) Tập hợp ℝ\ (– ∞; 3) là tập hợp các số thực không thuộc khoảng (– ∞; 3)

Vậy ℝ\ (– ∞; 3) = [3; + ∞) và được biểu diễn là:

d) Tập hợp (– 3; 2) \ [1; 3) gồm các phần tử thuộc (– 3; 2) và không thuộc [1; 3).

Vậy (– 3; 2) \ [1; 3) = (– 3; 1) và được biểu diễn là:

Xem thêm đáp án tại: Giải Toán 10 Bài 2: Tập hợp. Các phép toán trên tập hợp Cánh diều

Giải Toán 10 Bài 2: Tập hợp Chân trời sáng tạo

Bài 1 trang 20 SGK Toán 10 Chân trời

Viết các tập hợp sau đây dưới dạng liệt kê các phần tử:

a) A = {x ∈ ℤ| |x| < 5};

b) B = {x ∈ ℝ| 2x² – x – 1 = 0};

c) C = {x ∈ ℕ | x có hai chữ số}.

Lời giải

a) A = {x ∈ ℤ | |x| < 5}

Xét |x| < 5

⇔ x < 5 hoặc – x < 5

⇔ x < 5 hoặc x > - 5

Suy ra -5 < x < 5.

Mà x ∈ ℤ nên x ∈ {-4; -3; -2; -1; 0; 1; 2; 3; 4}.

Vậy A = {-4; -3; -2; -1; 0; 1; 2; 3; 4}.

b) Xét phương trình 2x² – x – 1 = 0

⇔ (x – 1) (2x + 1) = 0

⇔ \(\left\{\begin{array}{l}\;x\;-\;1\;=\;0\;\;\\2\;x\;+\;1\;=\;0\;\end{array}\right.\)

Mà 1; 1/2∈R

Vậy B = {1;1/2}

c) Các số tự nhiên có hai chữ số là 10; 11; 12; 13; 14; 15; …; 99.

Vậy C = {10; 11; 12; 13; 14; 15; …; 99}.

Bài 2 trang 22 SGK Toán 10 Chân trời

Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:

a. Tập hợp A = {1; 2; 3; 6; 9; 18};

b. Tập hợp B các nghiệm của bất phương trình 2x + 1 > 0;

c. Tập hợp C các nghiệm của phương trình 2x - y = 6.

Lời giải

a. A = {x ∈ N | x là ước của 18}

b. B = {x ∈ R | 2x + 1 > 0}

c. C = {x ∈ R , y ∈ R | 2x - y = 6}

Bài 3 trang 21 SGK Toán 10 Chân trời

Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập còn lại? Chúng có bằng nhau không?

a) A = {x ∈ ℕ | x < 2} và B = {x ∈ ℤ | x² – x = 0};

b) C là tập hợp các hình thoi và D là tập hợp các hình vuông;

c) E = (-1; 1] và F = (−∞;2]

Lời giải

a) các số tự nhiên thỏa mãn nhỏ hơn 2 là 0; 1.

Khi đó A = {0; 1}.

Xét phương trình x₂ – x = 0 ⇔\(\left\{\begin{array}{l}x=0\\x=1\end{array}\right.\)

Khi đó B = {0; 1}.

Suy ra các phần tử của tập hợp A thuộc tập hợp B nên A ⊂ B . Mặt khác các phần tử của tập hợp B cũng thuộc tập hợp A nên B ⊂ A.

Do đó A = B.

b) Ta có hình vuông là hình thoi

Suy ra D là tập con của tập C. Ta viết D ⊂ C .

Nhưng hình thoi chưa chắc là hình vuông. Suy ra tập C không là tập con của tập hợp D.

Do đó C khác D.

c) Ta có E = (-1; 1] = {x ∈ R| −1 < x ≤ 1} và F = (−∞;2] = {x ∈ R| x ≤ 2}

Suy ra các phần tử của tập hợp E thuộc tập hợp F nên E ⊂ F . Nhưng có phần tử của tập hợp F không thuộc tập hợp E chẳng hạn như -10 ∈ F mà -10 ∉ E nên F không là tập hợp con của E.

Do đó E không bằng F.

Xem thêm đáp án tại: Giải Toán 10 Bài 2: Tập hợp Chân trời sáng tạo

Giải Toán 10 Bài 2: Tập hợp và các phép toán trên tập hợp Kết nối tri thức

Bài 1.8 trang 19 SGK Toán 10 Kết nối

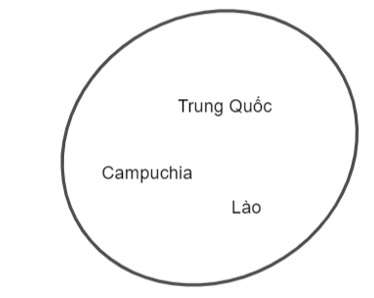
Gọi X là tập hợp các quốc gia tiếp giáp với Việt Nam. Hãy liệt kê các phần tử của tập hợp X và biểu diễn tập X bằng sơ đồ Ven.

Lời giải

Các quốc gia tiếp giáp với Việt Nam bao gồm: Trung Quốc, Lào, Campuchia.

⇒ X = {Trung Quốc, Lào, Campuchia}.

Biểu diễn tập hợp X bằng sơ đồ Ven, ta được:

Bài 1.9 trang 19 SGK Toán 10 Kết nối

Kí hiệu E là tập hợp các quốc gia tại khu vực Đông Nam Á.

a) Nêu ít nhất hai phần tử thuộc tập hợp E.

b) Nêu ít nhất hai phần tử không thuộc tập hợp E.

c) Liệt kê các phần tử thuộc tập hợp E. Tập hợp E có bao nhiêu phần tử?

Lời giải

a) Các phần tử thuộc tập hợp E là: Việt Nam, Singapore, Lào.

b) Các phần tử không thuộc tập hợp E là: Mĩ, Nga, Anh.

c) Các quốc gia tại khu vực Đông Nam Á bao gồm: Việt Nam, Lào, Campuchia, Thái Lan, Myanmar, Malaysia, Singapore, Indonesia, Brunei, Philippines và Đông Timor.

Khi đó tập hợp E = {Việt Nam, Lào, Campuchia, Thái Lan, Myanmar, Malaysia, Singapore, Indonesia, Brunei, Philippines, Đông Timor}.

Tập hợp E có tất cả 11 phần tử.

Bài 1.10 trang 19 SGK Toán 10 Kết nối

Hãy viết tập hợp sau bằng cách nêu tính chất đặc trưng cho các phần tử của tập hợp:

A = {0; 4; 8; 12; 16}.

Lời giải

Bằng cách nêu tính chất đặc trưng:

A = {x ∈ ℕ | x = 4k, x < 18, k ∈ ℕ}.

Bài 1.11 trang 19 SGK Toán 10 Kết nối

Trong các tập hợp sau, tập nào là tập rỗng?

A = { x ∈ ℝ | x² – 6 = 0};

B = { x ∈ ℤ | x² – 6 = 0};

Lời giải

Ta có: x² – 6 = 0

⇔\(\left\{\begin{array}{l}x=\surd6\\x=-\surd6\end{array}\right.\)

Vì −√6; √6 ∈ R nên A = {−√6;√6}

Vì −√6; √6 ∉ Z nên B = ∅.

Vậy tập hợp B là tập rỗng.

Xem thêm đáp án tại: Giải Toán 10 Bài 2: Tập hợp và các phép toán trên tập hợp Kết nối tri thức

C. Giải SBT Toán 10 Bài 2

Sách bài tập Toán 10 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:

• Giải bài tập Toán 10 SBT bài 2 chương 1

D. Bài tập trắc nghiệm Toán 10 Tập hợp

Để ôn tập lại kiến thức cũng như rèn luyện nâng cao hơn về bài tập của bài Tập hợp này, VnDoc xin gửi tới các bạn học sinh Tài liệu Bài tập về Tập hợp do VnDoc biên soạn. Qua đó sẽ giúp các bạn học sinh hiểu sâu hơn và nắm rõ hơn lý thuyết cũng như bài tập của bài học này. Mời các bạn học sinh tham khảo:

• Bài tập Toán 10 chương 1: Mệnh đề - Tập hợp
• Tập hợp và các phép toán tập hợp
• Bài tập Toán lớp 10 chương 1: Mệnh đề - Tập hợp

------------------------------------

Trên đây VnDoc đã giới thiệu tới các bạn bài Toán 10 Bài 2: Tập hợp. Mời bạn đọc cùng tham khảo thêm tại mục Ngữ Văn 10, Tiếng Anh lớp 10, Vật lý lớp 10,... được VnDoc.com chúng tôi biên soạn và tổng hợp.