Đề thi học kì 2 Toán 10 KNTT (Cấu trúc mới) năm 2025 Đề 2

Đề thi học kì 2 môn Toán 10 Kết nối tri thức

Đề thi học kì 2 lớp 10 môn Toán KNTT năm 2025 được VnDoc biên soạn được đưa ra dựa vào ma trận đề kiểm tra theo Công văn 7991 của Bộ Giáo dục và Đào tạo, áp dụng bắt đầu từ học kì 2 đối với THPT. Mời các bạn tham khảo chi tiết nội dung trong file tải về.

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 10.

Trường THPT Kết nối tri thức Đề thi thử số 2

ĐỀ KIỂM TRA CUỐI HỌC KỲ II MÔN: TOÁN - LỚP 10 NĂM HỌC: 2024 – 2025 Thời gian làm bài: 90 phút

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN

Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Trong mặt phẳng \(Oxy,\) cho đường tròn \((C)\) có phương trình: \((x - 1)^{2} + (y + 5)^{2} = 25.\) Đường tròn \((C)\) đi qua điểm nào trong các điểm dưới đây?

A. \(M(3; - 2).\)                    B. \(P(4; - 1).\)                     C. \(Q(2;1).\)              D. \(N( - 1;3).\)

Câu 2: Phương trình nào sau đây là phương trình chính tắc của hypebol?

A. \(\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1.\)                            B. \(\frac{x^{2}}{4} - \frac{y^{2}}{9} = - 1.\)

C. \(\frac{x^{2}}{4} - \frac{y^{2}}{9} = 1.\)                             D. \(\frac{x^{2}}{9} + \frac{y^{2}}{9} = 1.\)

Câu 3: Trong mặt phẳng \(Oxy,\) cho đường elip \((E)\) có phương trình chính tắc \(\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1.\) Tổng khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng

A. \(6\)                               B. \(3.\)                        C. \(5.\)                       D. \(12.\)

Câu 4: Có \(6\) nhà xe vận chuyển hành khách giữa Việt Trì và Hà Nội. Số cách để một người đi từ Việt Trì tới Hà Nội rồi sau đó quay lại Việt Trì bằng hai nhà xe khác nhau là

A. \(11.\)                            B. \(12.\)                       C. \(30.\)                           D. \(6.\)

Câu 5: Số cách sắp xếp \(9\) học sinh thành một hàng dọc là

A. \(9\).                             B. \(9^{9}\).                              C. \(C_{9}^{9}\).                       D. \(9!\)

Câu 6: Số nào dưới đây là nghiệm của phương trình \(\sqrt{2x^{2} + x + 3} = \sqrt{x^{2} + 2x + 5}\)?

A. \(x = - 3\).              B. \(x = - 2\).                   C. \(x = 1\).                    D. \(x = 2\).

Câu 7: Trong mặt phẳng \(Oxy\), vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục \(Oy\)?

A. \(\overrightarrow{u_{1}} = (1;0)\).             B. \(\overrightarrow{u_{4}} = (1;1)\).                C. \(\overrightarrow{u_{3}} = ( - 1;1)\).             D. \(\overrightarrow{u_{2}} = (0;1)\).

Câu 8: Từ các chữ số \(1;2;3;4;5;6;7\) lập ra được bao nhiêu số tự nhiên có 4 chữ số và các chữ số đôi một khác nhau?

A. \(A_{7}^{4}\).                         B. \(P_{7}\).                        C. \(C_{7}^{4}\).                      D. \(7^{4}\).

Câu 9: Gieo ngẫu nhiên một con súc sắc hai lần liên tiếp. Xét biến cố \(A\): “Lần thứ hai xuất hiện mặt ba chấm” thì biến cố \(A\) là

A. \(A = \{(3\ ;\ 1)\ ;\ (3\ ;\ 2)\ ;\ (3\ ;\ 3)\ ;\ (3\ ;\ 4)\ ;\ (3\ ;\ 5)\ ;\ (3\ ;\ 6)\}\).

B. \(A = \{(3\ ;\ 1)\ ;\ (3\ ;\ 2)\ ;\ (3\ ;\ 4)\ ;\ (3\ ;\ 5)\ ;\ (3\ ;\ 6)\}\).

C. \(A = \{(1\ ;\ 3)\ ;\ (2\ ;\ 3)\ ;\ (3\ ;\ 3)\ ;\ (4\ ;\ 3)\ ;\ (5\ ;\ 3)\ ;\ (6\ ;\ 3)\}\).

D. \(A = \left\{ (3\ ;\ 3) \right\}\).

Câu 10: Một hộp chứa sáu quả cầu trắng và bốn quả cầu đen. Lấy ngẫu nhiên đồng thời bốn quả. Xác suất sao cho có ít nhất một quả màu trắng là

A. \(\frac{1}{21}\).                    B. \(\frac{1}{210}\).                     C. \(\frac{209}{210}\).                 D. \(\frac{8}{105}\).

Câu 11: Trên giá sách có 5 quyển sách Toán, 4 quyển sách Lý và 3 quyển sách Hóa. Lấy ngẫu nhiên 3 quyển sách. Xác suất để 3 quyển sách được lấy ra thuộc 3 môn khác nhau là

A. \(\frac{8}{11}\).                   B. \(\frac{3}{11}\).                        C. \(\frac{1}{110}\).                   D. \(\frac{109}{110}\).

Câu 12: Tập hợp nào sau đây là tập nghiệm của bất phương trình \(x^{2} - 5x + 4 \leq 0\)?

A. \(S = (1;4)\).                                    B. \(S = \lbrack 1;4\rbrack\).

C. \(S = ( - \infty;1) \cup (4; + \infty)\).              D. \(S = ( - \infty;1\rbrack \cup \lbrack 4; + \infty)\).

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Tổ I của lớp 10A gồm có 7 học sinh gồm 4 nam và 3 nữ.

a) Xếp 7 học sinh của tổ I vào một hàng ngang để chụp ảnh có 7! cách.

b) Có \(C_7^2\) cách chọn ra một cặp nam nữ của tổ I để tham gia hát song ca.

c) Lớp trưởng cần chọn ra 3 học sinh của tổ I để trực nhật lớp, trong đó 1 bạn quét lớp, 1 bạn lau bảng, 1 bạn kê bàn ghế. Số cách chọn là \(A_7^3\) cách.

d) Có 720 cách xếp 7 học sinh của tổ I vào một hàng dọc sao cho 3 bạn nữ luôn đứng cạnh nhau.

Câu 2: Trong mặt phẳng tọa độ Oxy, cho đường hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\).

a) Hypebol (H) có tiêu cự bằng 10.

b) Hypebol (H) có một tiêu điểm là \({F_2}\left( {1;0;0} \right)\).

c) Điểm M(0; 6) thuộc hypebol (H).

d) Hiệu các khoảng cách từ một điểm bất kỳ nằm trên đường hypebol (H) đến hai tiêu điểm của (H) có giá trị tuyệt đối bằng 8.

PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN

Thí sinh trả lời từ câu 1 đến câu 4.

Câu 1: Bất phương trình \(6x^{2} + 5x < 5 - 8x\) có bao nhiêu nghiệm nguyên?

Câu 2: Đội thanh niên xung kích của một trường trung học phổ thông có \(12\) học sinh trong đó có \(9\) học sinh nam và \(3\) học sinh nữ. Đoàn trường cần chọn một nhóm \(5\) học sinh đi làm nhiệm vụ sao cho phải có \(1\) đội trưởng nam, \(1\) đội phó nam và có ít nhất \(1\) nữ. Hỏi có bao nhiêu cách chọn?

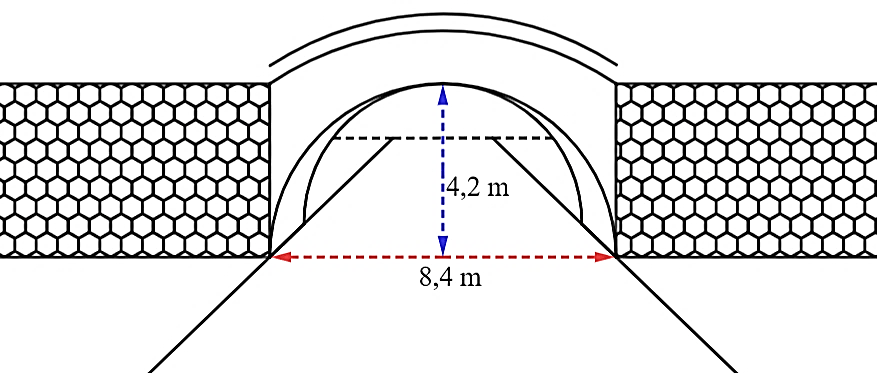
Câu 3: Một cánh cổng hình bán nguyệt rộng \(8,4\ m\) và cao \(4,2\ m\). Mặt đường dưới cổng được chia thành hai làn đều nhau cho xe ra vào. Một chiếc xe tải rộng \(2,8\ m\) không chở hàng nếu đi đúng làn đường quy định và có thể đi qua cổng mà không làm hư cổng thì chiều cao của xe không vượt quá bao nhiêu mét (làm tròn đến hàng phần trăm)?

Câu 4: Có \(20\) tấm thẻ được đánh số từ \(1\) đến \(20\). Chọn ngẫu nhiên ra \(8\) tấm thẻ, tính xác suất để có \(3\) tấm thẻ mang số lẻ, \(5\) tấm thẻ mang số chẵn trong đó chỉ có đúng \(1\) tấm thẻ mang số chia hết cho \(10.\)(Kết quả làm tròn đến hàng phần trăm).

PHẦN IV. TỰ LUẬN

Câu 1: Giải phương trình \(\sqrt{2x^{2} - 6x + 5} = 2x - 3\).

Câu 2: Một hiệu sách có 3 loại sách tham khảo môn Toán lớp 11, 2 loại sách tham khảo môn Văn lớp 11 và 2 loại sách tham khảo môn Anh lớp 11. Bạn An vào hiệu sách này muốn chọn một loại sách tham khảo kể trên để mua làm quà tặng sinh nhật bạn Bình. Vẽ sơ đồ hình cây minh họa và cho biết An có bao nhiêu cách chọn 1 loại sách tham khảo?

Câu 3: Từ các số 1,2,3,4,5 có bao nhiêu số gồm 8 chữ số sao cho chữ số 5 xuất hiện đúng 3 lần.

Câu 4: Lập phương trình đường thẳng \(\Delta\) đi qua điểm \(N(5;2)\) và song song với đường thẳng \(3x - 2y + 5 = 0.\)

Câu 5: Hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí \(A,\ \ B\) cách nhau \(200\ \ km.\) Tại cùng một thời điểm, hai trạm cùng phát tín hiệu với vận tốc \(292\ \ 000\ \ km/s\) để hai tàu thủy đang ở hai vị trí \(C,\ \ D\) thu và đo độ lệch thời gian. Với tàu thủy tại vị trí \(C,\) tín hiệu từ \(A\) đến sớm hơn tín hiệu từ \(B\) là \(0,0005\ \ s.\) Với tàu thủy tại vị trí \(D,\) tín hiệu từ \(B\) đến sớm hơn tín hiệu từ \(A\) là \(0,0005\ \ s.\) Tính hiệu khoảng cách từ tàu ở vị trí \(D\) đến hai trạm phát tín hiệu \(A\) và \(B\) từ đó tính khoảng cách từ tàu ở vị trí \(D\) đến trạm tín hiệu tại \(A\) biết hai tàu cách nhau \(300\ \ km\) và \(CD\) song song với \(AB\) (làm tròn đến hàng đơn vị).

Câu 6: Đề cương ôn tập môn Lịch sử có \(30\) câu. Đề thi được lập từ cách chọn ngẫu nhiên \(10\) câu trong \(30\) câu trong đề cương. Một học sinh chỉ học thuộc \(25\) câu trong đề cương. Xác suất để trong đề thi có ít nhất \(9\) câu hỏi nằm trong \(25\) câu mà học sinh đã học thuộc bẳng bao nhiêu? (Kết quả làm tròn đến hàng phần trăm).

- Hết -

------------------------------------------

Đáp án chi tiết có trong file tải