Đề thi học kì 2 Toán 10 KNTT (Cấu trúc mới) năm 2025 Đề 4

Đề thi học kì 2 môn Toán 10 Kết nối tri thức

Đề thi học kì 2 lớp 10 môn Toán KNTT năm 2025 được VnDoc biên soạn được đưa ra dựa vào ma trận đề kiểm tra theo Công văn 7991 của Bộ Giáo dục và Đào tạo, áp dụng bắt đầu từ học kì 2 đối với THPT. Mời các bạn tham khảo chi tiết nội dung trong file tải về.

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 10.

Trường THPT Kết nối tri thức Đề thi thử số 4

ĐỀ KIỂM TRA CUỐI HỌC KỲ II MÔN: TOÁN - LỚP 10 NĂM HỌC: 2024 – 2025 Thời gian làm bài: 90 phút

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN

Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Hai bạn lớp \(A\) và hai bạn lớp \(B\) được xếp vào \(4\) ghế ngồi thành một hàng ngang. Xác suất để hai bạn cùng lớp không ngồi cạnh nhau bằng

A. \(\frac{1}{2}\).                     B. \(\frac{2}{3}\).                          C. \(\frac{1}{4}\).                         D. \(\frac{1}{3}\).

Câu 2: Biết elip \((E)\) có khoảng cách giữa hai tiêu điểm bằng \(6\) và đi qua điểm có tọa độ \((4;0)\). Phương trình chính tắc của \((E)\) là

A. \((E):\frac{x^{2}}{16} + \frac{y^{2}}{7} = 1\).                           B. \((E):\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1\).

C. \((E):\frac{x^{2}}{16} - \frac{y^{2}}{7} = 1\).                           D. \((E):\frac{x^{2}}{16} + \frac{y^{2}}{9} = 1\).

Câu 3: Số cách xếp \(3\) học sinh nam và \(4\) học sinh nữ vào một dãy ghế hàng ngang có \(7\) chỗ ngồi là

A. \(7!\).                     B. \(4!.3!\).                            C. \(4!\).                 D. \(4!.3\).

Câu 4: Biểu thức \(P(x) = x^{5} - 10x^{4} + 40x^{3} - 80x^{2} + 80x - 32\) là khai triển của nhị thức nào sau đây?

A. \((x - 2)^{5}\).               B. \((x - 2)^{4}\).                 C. \((2x - 1)^{5}\).                    D. \((2x + 1)^{5}\).

Câu 5: Trong phép thử gieo một đồng xu liên tiếp 3 lần, số phần tử của không gian mẫu là

A. \(2\).                         B. \(4\).                              C. \(8\).                           D. \(16\).

Câu 6: Một hộp có 5 viên bi đen và 4 viên bi trắng. Chọn ngẫu nhiên hai viên bi. Xác suất để hai viên bi được chọn có đủ 2 màu là

A. \(\frac{5}{324}.\)                   B. \(\frac{5}{9}.\)                    C. \(\frac{2}{9}.\)                                 D. \(\frac{1}{18}.\)

Câu 7: Tổ 1 của lớp 10A1 có 3 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1 bạn học sinh của tổ 1 đi trực vệ sinh. Hỏi có bao nhiêu cách chọn.

A. \(15\).                     B. \(3^{5}\).                       C. \(8\).                         D. \(5^{3}\)

Câu 8: Bình có 5 cái áo khác nhau, 4 chiếc quần khác nhau, 3 đôi giày khác nhau và 2 chiếc mũ khác nhau. Số cách chọn một bộ gồm quần, áo, giầy và mũ của Bình là

A. 120.                  B. 60.                  C. 5.                        D. 14.

Câu 9: Trong mặt phẳng tọa độ \(Oxy\) cho đường tròn \((C)\) có tâm \(I(1; - 1)\) bán kính \(R = 5\). Biết rằng đường thẳng \((d):3x - 4y + 8 = 0\) cắt đường tròn \((C)\) tại hai điểm phân biệt \(A,B\). Tính độ dài đoạn thẳng \(AB\).

A. \(AB = 8\).                       B. \(AB = 4\).                  C. \(AB = 3.\).                D. \(AB = 6\).

Câu 10: Trong một lớp học có \(20\) học sinh nam và 15 học sinh nữ. Có bao nhiêu cách chọn ba học sinh làm ba nhiệm vụ: lớp trưởng, lớp phó và bí thư?

A. \(A_{35}^{3}\).                          B. \(35!\).                    C. \(A_{3}^{35}\).                      D. \(C_{35}^{3}\).

Câu 11: Trong mặt phẳng \(Oxy,\) phương trình đường trung tuyến \(AM\) của tam giác \(ABC\) với \(A( - 2;3)\), \(B(1; - 2)\), \(C( - 5;4)\) là

A. \(\left\{ \begin{matrix} x = 2 \\ y = 3 - 2t \\ \end{matrix} \right.\).                                     B. \(\left\{ \begin{matrix} x = - 2 - 4t \\ y = 3 - 2t \\ \end{matrix} \right.\).

C. \(\left\{ \begin{matrix} x = - 2t \\ y = - 2 + 3t \\ \end{matrix} \right.\).                                  D. \(\left\{ \begin{matrix} x = - 2 \\ y = 3 - 2t \\ \end{matrix} \right.\).

Câu 12: Bảng xét dấu nào sau đây là bảng xét dấu của tam thức \(f(x) = - x^{2} - x + 6\)?

A. .

B. .

C. .

D. .

PHẦN II. PHN TRẮC NGHIỆM ĐÚNG SAI

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Có 100 tấm thẻ được đánh số từ 1 đến 100. Lấy ngẫu nhiên 5 thẻ

a) Số phần tử của không gian mẫu là\(C_{100}^{5}\)

b) Xác suất để 5 thẻ lấy ra đều mang số chẵn là \(\frac{1}{2}\)

c) Xác suất để 5 thẻ lấy ra có ít nhất một thẻ mang số chia hết cho 3 xấp xỉ bằng 0,78.

d) Xác suất để 5 thẻ lấy ra có hai thẻ mang số chẵn và 3 thẻ mang số lẻ xấp xỉ bằng 0,32

Câu 2: Trên mặt phẳng tọa độ \(Oxy\) cho Parabol \((P)\) có phương trình dạng chính tắc. Biết \((P)\) có tiêu điểm là \(F(1;0)\).

a) Phương trình chính tắc của \((P)\) là \(y^{2} = 2x\).

b) Đường chuẩn của \((P)\) là \(\Delta:x - 1 = 0\).

c) \((P)\) qua \(A(1;4).\)

d) Trong các dây cung của \((P)\) qua tiêu điểm thì dây có độ dài nhỏ nhất là \(4\).

PHẦN III. CÂU HỎI TỰ LUẬN NGẮN

Thí sinh trả lời từ câu 1 đến câu 4.

Câu 1: Từ các chữ số \(0;1;2;3;4;5;6;7\) lập được bao nhiêu số có bốn chữ số khác nhau sao cho hai chữ số \(1\) và \(2\) luôn đứng cạnh nhau?

Câu 2: Để kiểm tra chất lượng sản phẩm từ công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp sữa cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp để phân tích mẫu. Xác suất để 3 hộp sữa được chọn có cả 3 loại là (kết quả làm tròn đến hàng phần trăm)

Câu 3: Điều hướng LORAN (điều hướng vô tuyến đường dài) cho máy bay và tàu thủy sử dụng các xung đồng bộ được truyền bởi các trạm phát đặt cách xa nhau. Các xung này di chuyển với tốc độ ánh sáng (186.000 dặm / giây). Sự chênh lệch về thời gian nhận được phản xạ của các xung này từ một máy bay hoặc tàu thủy là không đổi, nên máy bay hoặc con tàu sẽ nằm trên một hyperbol có các trạm phát là các tiêu điểm. Giả sử rằng hai trạm phát, cách nhau 300 dặm, được đặt trên một hệ tọa độ vuông góc tại các điểm có tọa độ \(( - 150;0)\) và \((150;0)\) và một con tàu đang đi trên một con đường là một nhánh của hypebol (xem hình vẽ).

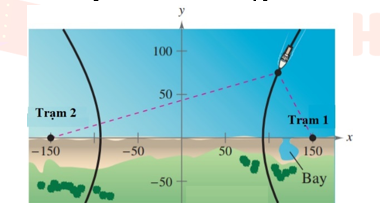
Biết rằng độ chênh lệch thời gian giữa các xung từ các trạm phát với con tàu là 1000 micro giây (0,001 giây). Xác định khoảng cách giữa tàu và trạm phát số 1 khi tàu vào bờ. (đơn vị dặm)

Câu 4: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình \(x^{2} + m^{2}x - 5m + 3 \leq 0\) có một nghiệm \(x = 1\)

PHẦN IV. TỰ LUẬN

Câu 1: Cho đường tròn \((C)\) có tâm \(I(1;2)\) và bán kính \(R = 3\).

a) Viết phương trình đường tròn.

b) Viết các phương trình tiếp tuyến của đường tròn \((C)\) biết tiếp tuyến vuông góc với đường thẳng \(3x - 4y + 1 = 0\).

Câu 2: Một hộp có \(20\) viên bi, trong đó có \(8\) viên bi đỏ được đánh số từ \(1\) đến \(8\), \(7\) viên bi xanh được đánh số từ \(1\) đến \(7\), \(5\) viên bi vàng được đánh số từ \(1\) đến \(5\). Một người lấy ngẫu nhiên trong hộp \(3\) viên bi.

a) Tính xác suất để \(3\) viên bi lấy ra có đủ cả \(3\) màu.

b) Tính xác suất để \(3\) viên bi lấy ra có đủ cả \(3\) màu và \(3\) số đôi một khác nhau.

Câu 3: a) Viết phương trình chính tắc của Hypebol \((H)\) biết \((H)\) đi qua điểm \(M\left( 2\sqrt{2};1 \right)\) và có tiêu cự bằng \(2\sqrt{5}\).

b) Tìm trên Elip \(\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1\) các điểm nhìn hai tiêu điểm của Elip theo một góc vuông.

- Hết -

------------------------------------------

Đáp án chi tiết có trong file tải