VnDoc.com

Đề thi học kì 2 Toán 10 KNTT (Cấu trúc mới) năm 2025 Đề 1

Đề thi hk2 toán 10 - Có đáp án chi tiết

Bài trước

Tải về

Bài sau

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Đề thi học kì 2 môn Toán 10 Kết nối tri thức

Đề thi học kì 2 lớp 10 môn Toán KNTT năm 2025 được VnDoc biên soạn được đưa ra dựa vào ma trận đề kiểm tra theo Công văn 7991 của Bộ Giáo dục và Đào tạo, áp dụng bắt đầu từ học kì 2 đối với THPT. Mời các bạn tham khảo chi tiết nội dung trong file tải về.

Đề thi cuối học kì 2 lớp 10 gồm có 4 phần:

Phần 1: Trắc nghiệm khách quan
Phần 2: Trắc nghiệm đúng sai
Phần 3: Câu hỏi tự luận ngắn
Phần 4: Tự luận.

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 10.

Trường THPT

Kết nối tri thức

Đề thi thử số 1

ĐỀ KIỂM TRA CUỐI HỌC KỲ II

MÔN: TOÁN - LỚP 10

NĂM HỌC: 2024 – 2025

Thời gian làm bài: 90 phút

Họ và tên học sinh: …………………………….. Lớp: …………………………..

PHẦN I. PHẦN TRẮC NGHIỆM KHÁCH QUAN NHIỀU LỰA CHỌN

Thí sinh trả lời từ câu 1 đến câu 20. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Hệ số của số hạng chứa $x^{2}y^{2}$ $x^{2}y^{2}$ trong khai triển của nhị thức Niu-tơn $(x + 2y)^{4}$ $(x + 2y)^{4}$ là

A. $32$. B. $24$. C. $8$. D. $16$.

Câu 2:Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường hyperbol?

A. $\frac{x^{2}}{25} + \frac{y^{2}}{16} = - 1.$ $\frac{x^{2}}{25} + \frac{y^{2}}{16} = - 1.$ B. $\frac{x^{2}}{16} + \frac{y^{2}}{25} = 1.$ $\frac{x^{2}}{16} + \frac{y^{2}}{25} = 1.$

C. $\frac{x^{2}}{16} - \frac{y^{2}}{25} = 1.$ $\frac{x^{2}}{16} - \frac{y^{2}}{25} = 1.$ D. $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1.$ $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1.$

Câu 3: Trong mặt phẳng $Oxy$, phương trình nào sau đây là phương trình đường tròn?

A. $x^{2} + y^{2} - 2x - 8y + 20 = 0$ $x^{2} + y^{2} - 2x - 8y + 20 = 0$. B. $4x^{2} + y^{2} - 10x - 6y - 2 = 0$ $4x^{2} + y^{2} - 10x - 6y - 2 = 0$.

C. $x^{2} + 2y^{2} - 4x - 8y + 1 = 0$ $x^{2} + 2y^{2} - 4x - 8y + 1 = 0$. D. $x^{2} + y^{2} - 4x + 6y - 12 = 0$ $x^{2} + y^{2} - 4x + 6y - 12 = 0$.

Câu 4: Trong mặt phẳng $Oxyz$, cho đường thẳng $\Delta:7x + 10y - 15 = 0$ $\Delta:7x + 10y - 15 = 0$. Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?

(I) Đường thẳng $\Delta$ $\Delta$ có một vectơ pháp tuyến là $(7;10)$.

(II) Đường thẳng $\Delta$ $\Delta$ đi qua điểm $M(1; - 2)$.

(III) Đường thẳng $\Delta$ $\Delta$ song song với đường thẳng $d:7x - 10y + 1 = 0$.

A. $0$. B. $1$.

C. $2$. D. $3$.

Câu 5: Bạn An vào một cửa hàng đồ uống để mua một loại thức uống. Cửa hàng có các sự lựa chọn về đồ uống được thể hiện ở sơ đồ sau.

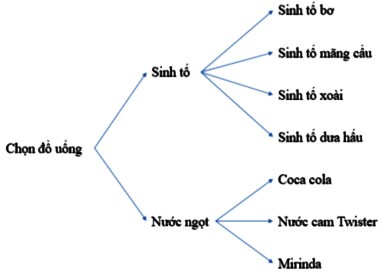
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?

(I). An có 4 cách chọn một loại sinh tố.

(II). An có 7 cách chọn một loại đồ uống.

(III). An có 14 cách chọn một loại đồ uống.

A. $0$. B. $1$. C. $2$. D. $3$.

Câu 6: Từ các số $\left\{ 2,3,4,5,6 \right\}$ $\left\{ 2,3,4,5,6 \right\}$ có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau?

A. $80$ B. $10$ C. $15$ D. $60$

Câu 7: Trong một trường THPT, khối 10 có 280 học sinh nam và 325 học sinh nữ. Nhà trường cần chọn một học sinh khối 10 đi dự đại hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?

A. $605$ B. $280$ C. $325$ D. $45$

Câu 8: Một nhóm học sinh gồm 6 học sinh nam và 4 học sinh nữ. Chọn ngẫu nhiên đồng thời 3 học sinh trong nhóm đó. Xác suất để trong 3 học sinh được chọn luôn có học sinh nữ

A. $\frac{1}{3}$ $\frac{1}{3}$. B. $\frac{5}{6}$ $\frac{5}{6}$. C. $\frac{2}{3}$ $\frac{2}{3}$. D. $\frac{1}{6}$ $\frac{1}{6}$.

Câu 9: Gieo 5 đồng xu cân đối, đồng chất. Xác suất để được ít nhất 1 đồng xu có mặt sấp bằng

A. $\frac{5}{11}$ $\frac{5}{11}$. B. $\frac{8}{11}$ $\frac{8}{11}$. C. $\frac{31}{32}$ $\frac{31}{32}$. D. $\frac{1}{32}$ $\frac{1}{32}$.

Câu 10: Phương trình chính tắc của elip có tổng các khoảng cách từ một điểm bất kỳ đến hai tiêu điểm bằng $10$ và có tiêu cự bằng $2\sqrt{5}$ $2\sqrt{5}$ là

A. $\frac{x^{2}}{10} + \frac{y^{2}}{2\sqrt{5}} = 1$ $\frac{x^{2}}{10} + \frac{y^{2}}{2\sqrt{5}} = 1$. B. $\frac{x^{2}}{25} + \frac{y^{2}}{20} = 1$ $\frac{x^{2}}{25} + \frac{y^{2}}{20} = 1$.

C. $\frac{x^{2}}{25} + \frac{y^{2}}{5} = 1$ $\frac{x^{2}}{25} + \frac{y^{2}}{5} = 1$. D. $\frac{x^{2}}{100} + \frac{y^{2}}{20} = 1$ $\frac{x^{2}}{100} + \frac{y^{2}}{20} = 1$.

Câu 11: Cho parabol $(P):y^{2} = 14x$ $(P):y^{2} = 14x$ có phương trình đường chuẩn $\Delta$ $\Delta$ là

A. $\Delta:x = - \frac{7}{2}$ $\Delta:x = - \frac{7}{2}$. B. $\Delta:x = \frac{7}{2}$ $\Delta:x = \frac{7}{2}$.

C. $\Delta:y = - \frac{7}{2}$ $\Delta:y = - \frac{7}{2}$. D. $\Delta:y = \frac{7}{2}$ $\Delta:y = \frac{7}{2}$.

Câu 12: Bất phương trình $mx^{2} - 2(m + 1)x + m + 7 < 0$ $mx^{2} - 2(m + 1)x + m + 7 < 0$ vô nghiệm khi

A. $m > \frac{1}{25}$ $m > \frac{1}{25}$. B. $m > \frac{1}{5}$ $m > \frac{1}{5}$.

C. $m \geq \frac{1}{4}$ $m \geq \frac{1}{4}$. D. $m \geq \frac{1}{5}$ $m \geq \frac{1}{5}$

PHẦN II. PHẦN TRẮC NGHIỆM ĐÚNG SAI

Thí sinh trả lời câu 1 và câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 1: Một bình đựng 16 viên bi, trong đó có 7 viên bi trắng, 6 viên bi đen và 3 viên bi đỏ. Lấy ngẫu nhiên 4 viên bi.

a) Số phần tử của không gian mẫu là $A_{16}^{4}$ $A_{16}^{4}$

b) Xác suất lấy được đúng bi trắng là $\frac{1}{52}$ $\frac{1}{52}$

c) Xác suất lấy được đủ 3 mầu là $\frac{9}{20}$ $\frac{9}{20}$

d) Xác suất lấy được đúng 2 mầu $\frac{11}{20}$ $\frac{11}{20}$

Câu 2: Trong mặt phẳng toạ độ, cho hypebol $(H)$có phương trình: $\frac{x^{2}}{9} - \frac{y^{2}}{16} = 1$ $\frac{x^{2}}{9} - \frac{y^{2}}{16} = 1$.

a) $a = 4$.

b) Điểm $M( - 3;0)$ nằm trên hypebol.

c) Tiêu cự của $(H)$ bằng 10.

d) Điểm $M(3a;\ 2a) \in (H)$ $M(3a;\ 2a) \in (H)$ thuộc góc phần tư thứ nhất. Diện tích tam giác $MF_{1}F_{2}$ $MF_{1}F_{2}$bằng $\frac{20\sqrt{3}}{3}$ $\frac{20\sqrt{3}}{3}$.

PHẦN III. CÂU HỎI TRẢ LỜI NGẮN

Thí sinh trả lời từ câu 1 đến câu 4.

Câu 1: Cho đường thẳng $d$ có phương trình $\sqrt{3}x + y = 0$ $\sqrt{3}x + y = 0$. Góc giữa đường thẳng $d$ và trục $Ox$ bằng bao nhiêu độ?

Câu 2: Trong mặt phẳng toạ độ $Oxy$, cho điểm $M$ thuộc đường thẳng $(d):\ \ x - 2y + 5 = 0$ $(d):\ \ x - 2y + 5 = 0$, điểm $N$ nằm trên elip $(E)$ có phương trình $\frac{x^{2}}{9} + \frac{y^{2}}{5} = 1$ $\frac{x^{2}}{9} + \frac{y^{2}}{5} = 1$ và điểm $A(2;\ 1)$ $A(2;\ 1)$. Khi đó giá trị nhỏ nhất $MA + MN$ bằng (kết quả làm tròn đến hàng phần trăm)

Câu 3: Chọn ngẫu nhiên 3 đỉnh trong một đa giác đều có 21 đỉnh. Tính xác suất để 3 đỉnh được chọn lập thành một tam giác cân nhưng không phải là tam giác đều. (Kết quả làm tròn đến chữ số thập phân thứ hai sau dấu phẩy)

Câu 4: Có $15$ học sinh giỏi gồm 6 học sinh khối 12; 4 học sinh khối 11 và 5 học sinh khối 10. Hỏi có bao nhiêu cách chọn ra 6 học sinh sao cho mỗi khối có ít nhất 1 học sinh?

PHẦN IV. TỰ LUẬN

Câu 1: Một câu lạc bộ gồm có $12$ vận động viên nam và $9$ vận động viên nữ. Huấn luyện viên muốn chọn ra $2$ vận động viên để đi thi đấu trong đó có $1$ nam và $1$ nữ. Hỏi huấn luyện viên có bao nhiêu cách chọn.

Câu 2: Một nhóm gồm $2$ học sinh lớp A, $4$ học sinh lớp B, $3$ học sinh lớp C được xếp thành hàng ngang. Hỏi có bao nhiêu cách xếp sao cho hai học sinh lớp A không đứng cạnh nhau và giữa hai học sinh lớp A chỉ có học sinh lớp C

Câu 3: Tìm $m$ để bất phương trình: $(m - 1)x^{2}–2(m - 2)x + 2 - m > 0$ $(m - 1)x^{2}–2(m - 2)x + 2 - m > 0$ vô nghiệm.

Câu 4: Lập phương trình chính tắc của elip đi qua điểm $N(5;0)$ và có tiêu cự bằng $2\sqrt{5}$ $2\sqrt{5}$.

Câu 5: Cho $(C):x^{2} + y^{2} - 4x + 6y + 5 = 0$ $(C):x^{2} + y^{2} - 4x + 6y + 5 = 0$ và đường thăng $d:x + y - 3 = 0$. Viết phương trình đường thẳng tiếp tuyến $\Delta$ $\Delta$ của $(C)$ biết nó song song với $d$?

Câu 6: Có 26 tấm thẻ được đánh số từ 1 đến 26. Rút ngẫu nhiên cùng một lúc 3 tấm thẻ. Tính xác suất sao cho tích của ba số trên 3 tấm thẻ là một số chẵn.

- Hết -

------------------------------------------

Đáp án chi tiết có trong file tải

Tải về

Chọn file muốn tải về: