Bài tập mệnh đề toán học lớp 10

Mệnh đề toán học lớp 10 là một trong những phần kiến thức mở đầu quan trọng trong chương trình Toán học phổ thông. Đây không chỉ là cơ sở để xây dựng tư duy logic, mà còn là nền tảng để học tốt các chuyên đề hình học, tổ hợp và mệnh đề logic ở các lớp học sau. Tuy nhiên, nhiều học sinh thường gặp khó khăn khi phân biệt các loại mệnh đề, viết mệnh đề đảo, mệnh đề phủ định, hay áp dụng trong chứng minh toán học. Trong bài viết này, chúng ta sẽ cùng ôn lại lý thuyết trọng tâm và luyện tập với bài tập mệnh đề toán học lớp 10 từ cơ bản đến nâng cao, có lời giải chi tiết để bạn dễ dàng tiếp thu và vận dụng hiệu quả vào thực tế học tập và thi cử. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

A. Bài tập ví dụ minh họa có hướng dẫn cụ thể về mệnh đề

Bài 1: Mệnh đề sau đúng, sai?

a) Điều kiện cần và đủ để \(a = 0\) là \(\frac{5}{a} = \frac{5}{b}\).

b) Điều kiện đủ để \(x > y\)là \(\sqrt{x} > \sqrt{y}\).

c) Điều kiện cần để tam giác ABC vuông là \(AB^{2} = BC^{2} - AC^{2}\).

d) Điều kiện đủ để \(\sqrt{x^{2}} = |x|\)là \(x \geq 0\).

Lời giải:

a) Nếu \(a = b\) thì \(\frac{5}{a} = \frac{5}{b}\): Mệnh đề sai.

b) Nếu \(\sqrt{x} > \sqrt{y}\) thì \(x > y\): Mệnh đề đúng.

c) Nếu tam giác ABC vuông thì \(AB^{2} = BC^{2} - AC^{2}\): Mệnh đề sai.

d) Nếu \(x \geq 0\) thì \(\sqrt{x^{2}} = |x|\): Mệnh đề đúng.

Bài 2: Trong các câu sau, câu nào là mệnh đề? Câu nào không phải là mệnh đề?

a) Phương trình \(3x^{2} - 5x + 2 = 0\) có nghiệm nguyên;

b) \(5 < 7 - 3\);

c) Có bao nhiêu dấu hiệu nhận biết hai tam giác đồng dạng?

d) Đấy là cách xử lí khôn ngoan!

Lời giải

Vì phương trình \(3x^{2} - 5x + 2 = 0\) có nghiệm nguyên \(x = 1\) nên câu a là đúng. Câu b là sai. Do đó, câu a và câu b là những mệnh đề.

Câu c là câu hỏi; câu d là câu cảm thán, nêu lên ý kiến của người nói. Do đó, không xác định được tính đúng sai. Vậy các câu c và d không phải là mệnh đề.

Bài 3: Cho tam giác \(ABC\). Lập mệnh đề \((P) \Rightarrow (Q)\) và mệnh đề đảo của nó, rồi xét tính đúng sai của chúng khi;

a. \((P):\) “Góc \(A\) bằng \(90^{0}\)” \((Q):\) “Cạnh \(BC\) lớn nhất”

b. \((P):\) “\(\widehat{A} = \widehat{B}\)” \((Q):\) “Tam giác \(ABC\) cân”.

Lời giải

Với tam giác \(ABC\) đã cho, ta có:

a. \((P) \Rightarrow (Q)\): “Nếu góc \(A\) bằng \(90^{0}\) thì cạnh \(BC\) lớn nhất” là mệnh đề đúng.

\((Q) \Rightarrow (P):\) “Nếu cạnh \(BC\) lớn nhất thì góc \(A\) bằng \(90^{0}\)”.

b. \((P) \Rightarrow (Q)\): “Nếu \(\widehat{A} = \widehat{B}\) thì tam giác \(ABC\) cân” là mệnh đề đúng.

\((Q) \Rightarrow (P):\) “Nếu tam giác \(ABC\) cân thì \(\widehat{A} = \widehat{B}\)” là mệnh đề sai, vì tam giác \(ABC\) chưa chắc cân tại \(C\).

Bài 4: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

Lời giải

A là mệnh đề sai: Ví dụ: \(1 + 3 = 4\) là số chẵn nhưng \(1,\ 3\) là số lẻ.

B là mệnh đề sai: Ví dụ: \(2.3 = 6\) là số chẵn nhưng \(3\) là số lẻ.

C là mệnh đề sai: Ví dụ: \(1 + 3 = 4\) là số chẵn nhưng \(1,3\) là số lẻ.

Bài 5: Trong các câu sau, câu nào là mệnh đề đúng?

A. Nếu \(a \geq b\) thì \(a^{2} \geq b^{2}.\)

B. Nếu \(a\) chia hết cho 9 thì \(a\) chia hết cho 3.

C. Nếu em chăm chỉ thì em thành công.

D. Nếu một tam giác có một góc bằng \(60^{0}\) thì tam giác đó đều.

Lời giải

Mệnh đề A là một mệnh đề sai vì \(b \leq a < 0\) thì \(b^{2} \geq a^{2}.\)

Mệnh đề B là mệnh đề đúng. Vì \(a \vdots 9 \Rightarrow \left\{ \begin{matrix} a = 9n,n\mathbb{\in Z} \\ 9 \vdots 3 \\ \end{matrix} \right.\ \Rightarrow a \vdots 3.\)

Câu C chưa là mệnh đề vì chưa khẳng định được tính đúng, sai.

Mệnh đề D là mệnh đề sai vì chưa đủ điều kiện để khẳng định một tam giác là đều.

B. Bài tập tự rèn luyện

Bài 1: Xét tính đúng sai của các mệnh đề sau:

a) Phương trình có hai nghiệm phân biệt.

b) 2k là số chẵn. (k là số nguyên bất kì)

c) 2¹¹ – 1 chia hết cho 11.

Bài 2: Cho tứ giác ABDC: Xét hai mệnh đề

P: Tứ giác ABCD là hình vuông.

Q: Tứ giác ABCD là hình chữ nhật có hai đường chéo bằng vuông góc với nhau.

Hãy phát biểu mệnh đề P ↔ Q bằng hai cách khác nhau, xét tính đúng sai của các mệnh đề đó.

Bài 3: Cho mệnh đề chứa biến P(n): n² – 1 chia hết cho 4 với n là số nguyên. Xét tính đúng sai của mệnh đề khi n = 5 và n = 2.

Bài 4: Nêu mệnh đề phủ định của các mệnh đề sau:

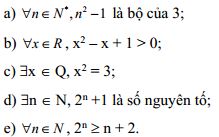
Bài 5: Xét tính đúng sai và nêu mệnh đề phủ định của các mệnh đề:

a) Tứ giác ABCD là hình chữ nhật.

b) 16 là số chính phương.

Bài 6: Cho tứ giác ABCD và hai mệnh đề:

P: Tổng 2 góc đối của tứ giác bằng 1800;

Q: Tứ giác nội tiếp được đường tròn.

Hãy phát biểu mệnh đề kéo theo P => Q và xét tính đúng sai của mệnh đề này.

Bài 7: Cho hai mệnh đề

P: 2k là số chẵn.

Q: k là số nguyên

Hãy phát biểu mệnh đề kéo theo và xét tính đúng sai của mệnh đề.

Bài 8: Hoàn thành mệnh đề đúng:

Tam giác ABC vuông tại A nếu và chỉ nếu ...................

- Viết lại mệnh đề dưới dạng một mệnh đề tương đương.

Bài 9: Xét tính đúng sai của các mệnh đề và viết mệnh đề phủ định của các mệnh đề.

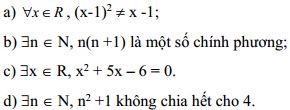
Bài 10: Xét tính đúng sai của các suy luận sau: (mệnh đề kéo theo)

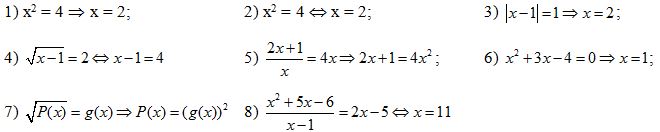
Bài 11: Phát biểu điều kiện cần và đủ để một:

• Tam giác là tam giác cân.
• Tam giác là tam giác đều.
• Tam giác là tam giác vuông cân.
• Tam giác đồng dạng với tam giác khác cho trước.
• Phương trình bậc 2 có hai nghiệm phân biệt.
• Phương trình bậc 2 có nghiệm kép.
• Số tự nhiên chia hết cho 2; cho 3; cho 5; cho 6; cho 9 và cho 11.

Bài 12: Chứng mình rằng: Với hai số dương a, b thì a + b ≥ 2√ab.

Bài 13: Xét tính đúng sai của mệnh đề:

Nếu một số tự nhiên chia hết cho 15 thì chia hết cho cả 3 và 5.

Bài 14: Phát biểu và chứng minh định lí sau:

a) n là số tự nhiên, n2 chia hết cho 3 thì n cũng chia hết cho 3.

b) n là số tự nhiên, n2 chia hết cho 6 thì n cũng chia hết cho cả 6; 3 và 2.

(Chứng minh bằng phản chứng)

Bài 15: Các câu sau: câu nào là mệnh đề, câu nào không phải mệnh đề? Nếu là mệnh đề hãy cho biết mệnh đề đó đúng hay sai.

a. Không được đi lối này.

b. Hôm nay là ngày bao nhiêu nhỉ?

c. 5 là số nguyên tố.

d. Hai tam giác bằng nhau thì có diện tích bằng nhau.

e. Phương trình \(12x^2-8x+17=0\) vô nghiệm.

f. Tam giác đều là tam giác có 3 góc bằng \(60^0\)

Câu 16: Lập mệnh đề phủ định và xét tính đúng sai của mệnh đề đó: 

\(a.\exists x\in \mathbb{Q},{{x}^{2}}-9=0\)

\(b. \forall x\in \mathbb{N},{{n}^{2}}>n\)

\(c. \forall x\in \mathbb{R},{{x}^{2}}>4\)

\(d. \exists x\in \mathbb{Q},{{x}^{2}}=1\)

\(e. \forall x\in \mathbb{R},{{x}^{2}}+4x-5>0\)

Câu 17: Phát biểu định lí sau theo thuật ngữ " điều kiện cần và đủ"

a. Tam giác vuông khi và chỉ khi _{\(AB^2+AC^2=BC^2\).}

b. Tứ giác nội tiếp trong đường tròn khi và chỉ khi có 2 góc đối bù nhau.

c. Một tam giác là tam giác đề khi và chỉ khi nó có 3 góc bằng.

d. Một số chia hết cho 5 khi và chỉ khi nó có chữ số tận cùng là 0 hoặc 5.

Câu 18: Chứng minh bằng phương pháp phản chứng: " Nếu hai số nguyên dương có tổng bình phương chia hết cho 3 thì cả hai số đó cùng chia hết cho 3."

Câu 19: Chứng minh bằng phản chứng: 

a. Nếu x, y là 2 số dương thì a + b ≥ 2ab.

b. Trong một tứ giác lồi phải có ít nhất một góc không nhọn và có ít nhất một góc không tù.

Câu 20: Các mệnh đề dưới đây thuộc mệnh đề gì và hãy nói nó đúng hay sai:

a) Nếu số a chia hết cho 3 thì a chia hết cho 6.

b) Nếu Δ ABC cân tại A thìΔABC có AB = AC.

c) Tứ giác ABCD là hình vuông khi và chỉ khi ABCD là hình chữ nhật và có AC vuông góc với BD.

Câu 21: Cho ΔABC, xét hai mệnh đề:

P: "ΔABC vuông cân tại A"

Q: "ΔABC là tam giác vuông có AB =AC"

Phát biểu mệnh đề P ⇔ Q bằng hai cách và cho biết mệnh đề này đúng hay sai.

Câu 22: Cho mệnh đề chứa biến P(n): "n(n+1) là số lẻ" với n là số nguyên. Hãy phát biểu các mệnh đề:

a) "∀n ∈ Z ,P(n)" và mệnh đề phủ định của nó.

b) "∃n ∈ Z ,P(n)" và mệnh đề phủ định của nó.

Câu 23: Xét xem các mệnh đề sau đây đúng hay sai và nêu mệnh đề phủ định của mỗi mệnh đề đó:

a)∀n ∈ N*, n (n2 - 1 ) là bội số của 3.

b)∀x ∈ R, x2 - 6x + 15 > 0

c) ∃x ∈ R: x2 - 6x + 5 = 0

d)∀x ∈ R,∃y ∈ R:y = x + 3

e)∀x ∈ R; ∀y ∈ R: x/y+y/x≥2

f) ∃n ∈ N, 2n - 1 là số nguyên tố.

Câu 24: Phát biểu dưới dạng "điều kiện cần" đối với các mệnh đề sau:

a) Hai góc đối đỉnh thì bằng nhau.

b) Hai tam giác có hai cặp cạnh bằng nhau kèm giữa một cặp góc bằng nhau thì bằng nhau.

c) Hai tam giác có hai cặp góc bằng nhau thì bằng nhau.

d) Một số chia hết cho 3 khi và chỉ khi tổng các chữ số chia hết cho 3.

-------------------------------------------------