Cho hình vuông ABCD tâm O tính độ dài vecto
Cách tính độ dài vecto Toán 10
Trong hình học phẳng, việc tính độ dài vectơ là một kỹ năng quan trọng, đặc biệt khi làm việc với các hình cơ bản như hình vuông. Trong bài viết này, chúng ta sẽ cùng tìm hiểu cách tính độ dài vectơ trong hình vuông ABCD có tâm O, áp dụng các kiến thức hình học cơ bản như tọa độ, định lý Pythagore và vectơ. Hãy cùng khám phá từng bước giải bài toán một cách rõ ràng và dễ hiểu!
Tính độ dài vecto môn Toán lớp 10 tổng hợp các dạng bài tập và hướng dẫn chi tiết về bất phương trình phổ biến trong các kì thi, bài kiểm tra trong chương trình trọng tâm Toán 10 nhằm giúp các bạn nắm vững kiến thức cơ bản, nâng cao kĩ năng tư duy bài tập. Chúc các bạn ôn tập hiệu quả!
Cho hình vuông ABCD tâm O
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại
A. Cách tính độ dài vecto
Định nghĩa: Mỗi vecto đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vecto đó. Độ dài của vecto 
\(\overrightarrow a\) được ký hiệu là \(\left| {\overrightarrow a } \right|\)
Ta có độ dài các vecto \(\overrightarrow {AB} ,\overrightarrow {CD} ,\overrightarrow {EF} ,....\) được biểu diễn như sau: \(\left| {\overrightarrow {AB} } \right| = AB;\left| {\overrightarrow {CD} } \right| = CD;\left| {\overrightarrow {EF} } \right| = EF,...\)
- Quy tắc hình bình hành: Tổng hai vectơ cạnh chung điểm đầu của một hình bình hành bằng vectơ đường chéo có cùng điểm đầu đó.
- Phương pháp: muốn tính độ dài vectơ, ta tính độ dài cách giữa điểm đầu và điểm cuối của vectơ.
- Trong hệ tọa độ: Cho \(\overrightarrow a = \left( {{a_1};{a_2}} \right)\). Khi đó độ dài vectơ \(\left| {\overrightarrow a } \right| = \sqrt {{a_1}^2 + {a_2}^2}\)
B. Công thức tính khoảng cách giữa hai điểm trong hệ tọa độ
Áp dụng công thức sau
Trong mặt phẳng tọa độ, khoảng cách giữa hai điểm \(A\left( {{x_A},{y_A}} \right);B\left( {{x_B};{y_B}} \right)\) là
\(\overrightarrow {AB} = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {y_B} - {y_A}\right)}^2}}\)
C. Bài tập ví dụ minh họa có hướng dẫn chi tiết
Bài tập 1: Cho hình vuông ABCD tâm O cạnh a. Tính độ dài các vecto sau:
| a. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) |
b. \(\left| {\overrightarrow {AC} + \overrightarrow {DC} } \right|\) |
| c. \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|\) |
d. \(\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right|\) |
Hướng dẫn giải
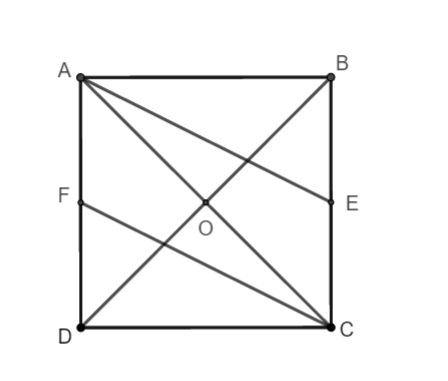
Giả sử E, F lần lượt là trung điểm của BC và AD
a. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2\left| {\overrightarrow {AE} } \right| = 2AE\)
Xét tam giác ABE vuông tại B, áp dung định lí Pitago ta có:
\(\begin{matrix}
A{E^2} = A{B^2} + B{E^2} \hfill \\
\Rightarrow AE = \sqrt {A{B^2} + B{E^2}} = \sqrt {{a^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 5 }}{2} \hfill \\
\end{matrix}\)
b. \(\left| {\overrightarrow {AC} + \overrightarrow {DC} } \right| = \left| {\overrightarrow {AC} + \overrightarrow {AB} } \right| = 2.AE = \frac{{a\sqrt 5 }}{2}\left( {cmt} \right)\)
c. \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = 2\left| {\overrightarrow {AO} } \right| = 2AO\)
Tam giác ABD vuông cân tại A, AO là đường cao. Áp dụng hệ thức lượng trong tam giác ta có:
\(\begin{matrix}
\dfrac{1}{{A{O^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{D^2}}} \hfill \\
\Rightarrow AO = \dfrac{{a\sqrt 2 }}{2} \hfill \\
\end{matrix}\)
d. \(\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right| = \left| {\overrightarrow {AO} + \overrightarrow {OC} + \overrightarrow {BO} + \overrightarrow {OD} } \right|\)
\(= \left| {\left( {\overrightarrow {AO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {BO} + \overrightarrow {OD} } \right)} \right| = \left| {\overrightarrow {AD} + \overrightarrow {BC} } \right| = 2.\left| {\overrightarrow {AD} } \right| = 2.AD = 2a\)
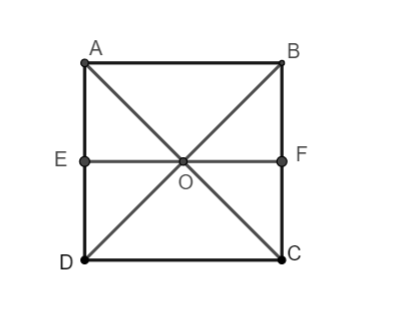
Bài tập 2: Cho hình vuông ABCD cạnh a tâm O. Tính \(\left| {\overrightarrow {AB} + \overrightarrow {OD} } \right|,\left| {\overrightarrow {AB} - \overrightarrow {OC} + \overrightarrow {OD} } \right|\), \(\left| {\overrightarrow {KA} - \overrightarrow {KB} - \overrightarrow {KC} + \overrightarrow {KD} } \right|\) với k bất kì, \(\left| {\overrightarrow {OA} - \overrightarrow {CB} } \right|,\left| {\overrightarrow {AB} + \overrightarrow {DC} } \right|\)
Hướng dẫn giải
a. \(\left| {\overrightarrow {AB} + \overrightarrow {OD} } \right| = \left| {\overrightarrow {AO} + \overrightarrow {OB} + \overrightarrow {OD} } \right| = \left| {\left( {\overrightarrow {OB} + \overrightarrow {OD} } \right) + \overrightarrow {AO} } \right| = \left| {\overrightarrow {AO} } \right| = AO = \frac{1}{2}AC\)
Tam giác ABD vuông cân tại A, AO là đường cao. Áp dụng hệ thức lượng trong tam giác ta có:
\(\begin{matrix}
\dfrac{1}{{A{O^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{D^2}}} \hfill \\
\Rightarrow AO = \dfrac{{a\sqrt 2 }}{2} \hfill \\
\end{matrix}\)
b. \(\left| {\overrightarrow {AB} - \overrightarrow {OC} + \overrightarrow {OD} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {CO} + \overrightarrow {OD} } \right| = \left| {\overrightarrow {AB} + \left( {\overrightarrow {CO} + \overrightarrow {OD} } \right)} \right| = \left| {\overrightarrow {AB} + \overrightarrow {CD} } \right| = \overrightarrow 0\)
(Do 2 vecto cùng phương, ngược chiều)
c. Gọi E, F lần lượt là trung điểm của AD, BC, ta dễ dàng suy ra O là trung điểm của EF.
\(\left| {\overrightarrow {KA} - \overrightarrow {KB} - \overrightarrow {KC} + \overrightarrow {KD} } \right| = \left| {\left( {\overrightarrow {KA} + \overrightarrow {KD} } \right) - \left( {\overrightarrow {KB} + \overrightarrow {KC} } \right)} \right|\)
\(= \left| {\overrightarrow {2KE} + \overrightarrow {2KF} } \right| = 2.\left( {\left| {\overrightarrow {KE} + \overrightarrow {KF} } \right|} \right) = 2.\left| {\overrightarrow {KO} } \right|\)
Bài tập 3: Cho tam giác \(ABC\) có tọa độ ba đỉnh \(A(6;3),B( - 3;6),C(1; -
2)\). Xác định tọa độ điểm \(D \in
BC\) thỏa mãn \(BD = 2CD\)?
Hướng dẫn giải
Giả sử tọa độ điểm D là: \(D(x;y)\)
Ta có: \(D \in BC\) thỏa mãn \(BD = 2CD\)
\(\Leftrightarrow \overrightarrow{BD} =
2\overrightarrow{DC}\)
Ta có: \(\left\{ \begin{matrix}
\overrightarrow{BD} = (x + 3;y - 6) \\
\overrightarrow{DC} = (1 - x; - 2 - y) \\
\end{matrix} \right.\)
\(\overrightarrow{BD} =
2\overrightarrow{DC} \Leftrightarrow \left\{ \begin{matrix}
x + 3 = 2 - 2x \\
y - 6 = - 4 - 2y \\
\end{matrix} \right.\)
\(\Leftrightarrow \left\{ \begin{matrix}
x = - \frac{1}{3} \\
y = \frac{2}{3} \\
\end{matrix} \right.\ \Rightarrow D\left( - \frac{1}{3};\frac{2}{3}
\right)\)
Bài tập 4: Trong hệ tọa độ \(Oxy\), cho các điểm \(A(0;1),B(1;3),C(2;7)\). Xác định tọa độ điểm \(N\) thỏa mãn biểu thức \(\overrightarrow{AB} =
2\overrightarrow{AN} + 3\overrightarrow{CN}\)?
Hướng dẫn giải
Theo bài ra ta có:
\(\overrightarrow{AB} =
2\overrightarrow{AN} + 3\overrightarrow{CN}\)
\(\Leftrightarrow \overrightarrow{AO} +
\overrightarrow{OB} = 2\overrightarrow{AO} + 2\overrightarrow{ON} +
3\overrightarrow{CO} + 3\overrightarrow{ON}\)
\(\Leftrightarrow \overrightarrow{ON} =
\frac{1}{5}\left( \overrightarrow{OA} + \overrightarrow{OB} +
2\overrightarrow{OC} \right)\)
\(\Rightarrow N\left( \frac{1 +
6}{5};\frac{1 + 3 + 21}{5} \right) = \left( \frac{7}{5};5
\right)\)
Bài tập 5: Cho hình thang \(ABCD;\left(
\widehat{A} = \widehat{D} = 90^{0} \right)\) có \(CD = 2AD = 2AB\). Gọi \(E;F\) lần lượt là các điểm thuộc đoạn \(AB;AC\) sao cho \(AB = 3AE\) và \(FC = 2FB\). Hãy tính tích vô hướng của hai vecto \(\overrightarrow{DE}\) và \(\overrightarrow{EF}\)?
Hướng dẫn giải
Hình vẽ minh họa
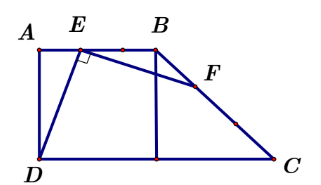
Ta có:
\(\overrightarrow{AE} =
\frac{1}{3}\overrightarrow{AB};\overrightarrow{DC} =
2\overrightarrow{AB}\) khi đó \(\overrightarrow{DE} = \overrightarrow{AE} -
\overrightarrow{AD} = \frac{1}{3}\overrightarrow{AB} -
\overrightarrow{AD}\ \ \ (1)\)
\(\overrightarrow{BF} =
\frac{1}{2}\overrightarrow{BC} = \frac{1}{3}\left( \overrightarrow{BA} +
\overrightarrow{AD} + \overrightarrow{DC} \right) =
\frac{1}{3}\overrightarrow{AB} +
\frac{1}{3}\overrightarrow{AD}\)
\(\overrightarrow{EF} =
\overrightarrow{EB} + \overrightarrow{BF} =
\frac{2}{3}\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AB} +
\frac{1}{3}\overrightarrow{AD}\)
\(= \overrightarrow{AB} +
\frac{1}{3}\overrightarrow{AD}\ \ \ (2)\)
Ta có: \(AB\bot AD \Leftrightarrow
\overrightarrow{AB}.\overrightarrow{AD} = 0\)
Xét \(\overrightarrow{DE}.\overrightarrow{EF} = \left(
\frac{1}{3}\overrightarrow{AB} - \overrightarrow{AD} \right).\left(
\overrightarrow{AB} + \frac{1}{3}\overrightarrow{AD}
\right)\)
\(= \frac{1}{3}{\overrightarrow{AB}}^{2} +
\frac{1}{9}\overrightarrow{AB}.\overrightarrow{AD} -
\overrightarrow{AD}.\overrightarrow{AB} -
\frac{1}{3}{\overrightarrow{AD}}^{2}\)
\(= \frac{1}{3}{\overrightarrow{AB}}^{2} -
\frac{1}{3}{\overrightarrow{AD}}^{2} = \frac{1}{3}AB^{2} -
\frac{1}{3}AD^{2} = 0\).
D. Bài tập tự rèn luyện
Bài 1: Cho hình vuông ABCD tâm O, cạnh a
Hãy xác định và tính độ dài của các vectơ \(\overrightarrow {OA} + \overrightarrow {OC} ;\overrightarrow {AB} + \overrightarrow {AC}\)
Bài 2: Cho tam giác ABC, xác định các vectơ \(\overrightarrow {AB} + \overrightarrow {CA} ,\overrightarrow {AB} + \overrightarrow {CA} + \overrightarrow {BC}\)
Bài 3: Cho 4 điểm A , B , C , D tuỳ ý. Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB}\)
Bài 4: Cho tứ giác ABCD . Gọi O là trung điểm của AB. Chứng minh rằng:\(\overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {AD} + \overrightarrow {BC}\)
Bài 5: Cho tam giác ABC, gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB. Chứng minh rằng: \(\overrightarrow {AD} + \overrightarrow {BE} + \overrightarrow {CF} = \overrightarrow 0\)
Bài 6: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng: \(\overrightarrow {MQ} = \overrightarrow {NP}\)
Bài 7: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của DC, AB, P là giao điểm của AM, BD, Q là giao điểm của AN và BD. Chứng minh rằng \(\overrightarrow {DM} = \overrightarrow {NB}\) và \(\overrightarrow {DP} = \overrightarrow {PQ}\)
---------------------------------------------------------------
Qua bài viết trên, bạn đã biết cách tính độ dài vectơ trong hình vuông ABCD có tâm O bằng các phương pháp hình học cơ bản. Việc hiểu rõ khái niệm vectơ và cách áp dụng vào các hình học quen thuộc sẽ giúp bạn nâng cao kỹ năng giải toán hiệu quả hơn. Đừng quên luyện tập thêm nhiều bài tương tự để nắm vững kiến thức này nhé!
