Cách tính tổ hợp
Công thức tính tổ hợp
Tổ hợp là một phần kiến thức quan trọng trong chương trình Toán lớp 10, thường xuất hiện trong các bài toán đếm và xác suất cơ bản. Tuy nhiên, nhiều học sinh vẫn gặp khó khăn khi phân biệt tổ hợp với chỉnh hợp và ghi nhớ công thức đúng cách. Bài viết dưới đây sẽ giúp bạn hiểu rõ cách tính tổ hợp Toán 10, cách áp dụng công thức vào bài tập thực tế, đồng thời cung cấp các mẹo học nhanh, nhớ lâu để tự tin chinh phục mọi dạng đề.
1. Tổ hợp chập k của n
Giả sử tập A có n phần tử 
\((n \geq
1)\) . Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.
Chú ý: Quy ước tập rỗng là tổ hợp chập 0 của n phần tử
2. Công thức tổ hợp
Gọi \(C_{n}^{k}\) là số các tổ hợp chập k của n phần tử \((1 \leq k \leq
n)\) . Khi đó:
Định lí:
\(C_{n}^{k} = \frac{n!}{k!(n -
k)!}\)
3. Tính chất cần nhớ
a. Tính chất 1
\(C_{n}^{k} = C_{n}^{n - k}\)
b. Tính chất 2 (công thức Paxcan)
\(C_{n - 1}^{k - 1} + C_{n - 1}^{k} =
C_{n}^{k}\)
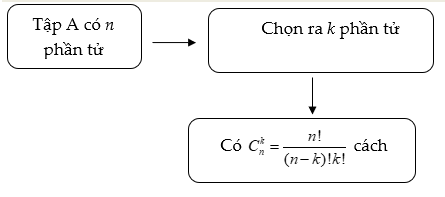
Lưu ý đối với học sinh: cần phân biệt được hai khái niệm chỉnh hợp và tổ hợp. Có thể phân biệt hai khái niệm bằng hai sơ đồ sau
4. Sơ đồ tư duy Tổ hợp
Ví dụ 1. Cho hình lục giác ABCDEF, hãy tìm một đoạn thẳng mà điểm đầu và điểm cuối chọn từ các đỉnh A, B, C, D, E, F và hãy tính xem có bao nhiêu đoạn thẳng như vậy.
Hướng dẫn giải
Ta có sơ đồ bài toán như sau
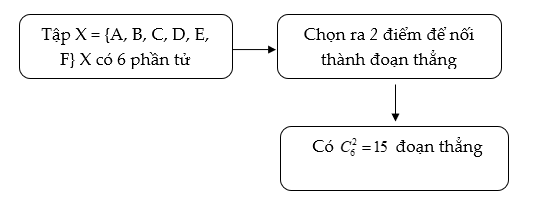
Hai điểm A và B tạo nên đoạn thẳng AB
Số đoạn thẳng bằng: \(C_{6}^{2} =
15\)
Ví dụ 2. Một nhóm học sinh nam gồm 6 em, muốn chia thành 3 cặp để khiêng bàn. Hỏi có bao nhiêu cách chia 6 học sinh trên thành 3 cặp.
Hướng dẫn giải
Công việc chia 6 học sinh thành 3 cặp có thể thực hiện theo 3 bước như sau
Bước 1. Chọn một cặp trong 6 học sinh có \(C_{6}^{2} = 15\) cách chọn
Bước 2. Chọn một cặp trong 4 học sinh còn lại có \(C_{4}^{2} = 6\) cách chọn
Bước 3. Hai học sinh còn lại là một cặp thứ 3
Vậy có 15.6 = 90 cách chia 6 học sinh thành 3 cặp.
--------------------------------
Với những kiến thức và ví dụ minh họa rõ ràng trong bài viết, bạn chắc chắn đã nắm vững cách tính tổ hợp Toán 10 một cách dễ hiểu và chính xác. Đừng quên luyện tập thường xuyên và vận dụng linh hoạt các công thức tổ hợp trong quá trình làm bài để đạt kết quả học tập tốt nhất. Tổ hợp không khó – chỉ cần hiểu đúng và luyện đúng, bạn sẽ thành thạo nhanh chóng!
