Cách tính chỉnh hợp
Công thức tính chỉnh hợp Toán 10
Trong chương trình toán học phổ thông, chỉnh hợp là một trong những kiến thức cơ bản và quan trọng thuộc chuyên đề tổ hợp. Việc hiểu rõ công thức chỉnh hợp và biết cách tính chỉnh hợp sẽ giúp bạn giải nhanh các bài toán đếm, sắp xếp và lựa chọn thứ tự. Bài viết dưới đây sẽ trình bày chi tiết định nghĩa, công thức, ví dụ minh họa và các lưu ý quan trọng giúp bạn học nhanh – nhớ lâu
1. Định nghĩa chỉnh hợp
Cho tập A gồm n phần tử 
\((n \geq
1)\). Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
2. Công thức của chỉnh hợp
Gọi \(A_{n}^{k}\) là số các chỉnh hợp chập k của n phần tử \((1 \leq k \leq
n)\) .
Ta có định lí sau
\(A_n^k = n.(n - 1)...(n - k + 1) = \frac{{n!}}{{(n - k)!}}\)
Chú ý:
a. Quy ước \(0! = 1\)
b. Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử.
Do đó: \(P_{n} = A_{n}^{n} =
n!\)
3. Sơ đồ tư duy tính chỉnh hợp
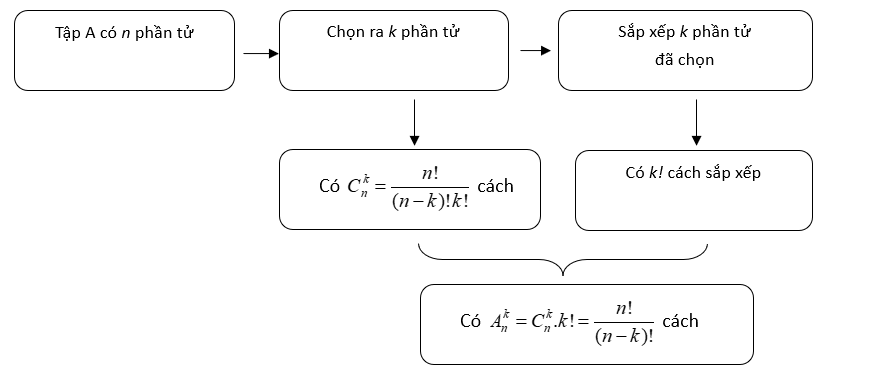
Ví dụ. Cho hình lục giác ABCDEF, hãy tìm một vectơ khác \(\overrightarrow{0}\) mà điểm đầu và điểm cuối chọn từ các đỉnh A, B, C, D, E, F và hãy tính xem có bao nhiêu vectơ như vậy.
Gợi ý:
Ta có sơ đồ bài toán như sau
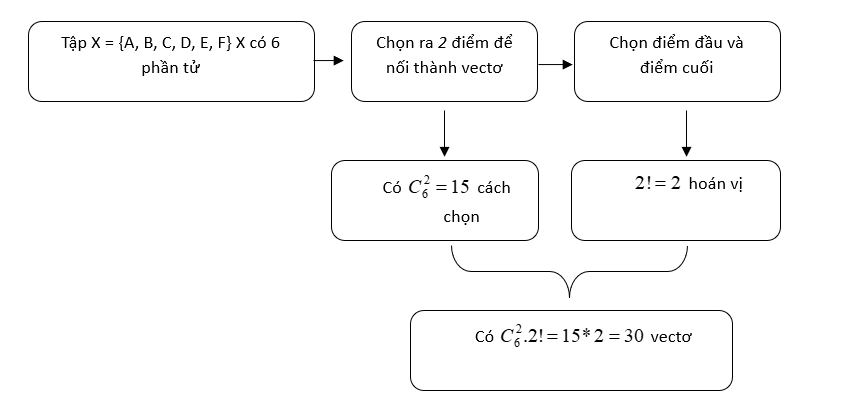
Hướng dẫn giải
Từ hai điểm A, B có hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{BA}\)
Số vectơ: \(A_{6}^{2} = 30\) vectơ.
------------------------------------------------
Trên đây là toàn bộ kiến thức cần thiết về công thức chỉnh hợp và cách tính chỉnh hợp giúp bạn học nhanh, hiểu sâu và áp dụng hiệu quả trong các bài tập tổ hợp. Đừng quên luyện tập nhiều dạng bài để củng cố kiến thức và nâng cao kỹ năng giải toán. Chúc bạn học tốt và đạt kết quả cao trong các kỳ thi!
