Đề thi giải toán trên Máy tính cầm tay lớp 9 THCS tỉnh Quảng Ninh năm 2011 - 2012

Đề thi giải toán trên Máy tính cầm tay lớp 9 THCS

Đề thi giải toán trên Máy tính cầm tay lớp 9 THCS tỉnh Quảng Ninh năm 2011 - 2012 có đáp án là tài liệu ôn thi hữu ích dành cho các em học sinh lớp 9, đề thi gồm 10 câu hỏi, mời các em tham khảo. Đây cũng là tài liệu hữu ích dành cho quý giáo viên sử dụng để làm bài tập nâng cao dành cho các em học sinh.

Bài tập trắc nghiệm môn Toán lớp 9

Tuyển tập đề thi học sinh giỏi môn toán lớp 9

ĐỀ THI MÔN: TOÁN (BẢNG A)

Bài 1: (6,0 điểm)

Tính gần đúng (làm tròn đến chữ số thập phân thứ 9)

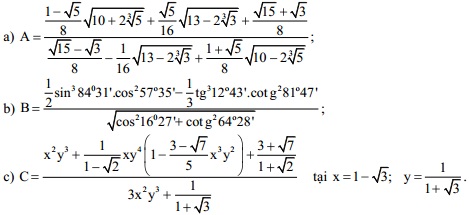
Bài 2: (4,0 điểm)

Tìm chữ số thập phân thứ 3²⁰¹³ của 16/23

Bài 3: (5,0 điểm)

Viết các số chính phương liên tiếp 1²; 2²; 3² ...; 2012² liền nhau ta được số D = 1491625...4048144.

a) Tìm số chữ số của D;

b) Tìm số dư trong phép chia D cho 9.

Bài 4: (6,0 điểm)

Cho dãy số: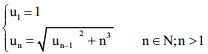

Gọi S_n là tổng n số hạng đầu tiên của dãy u_n (S_n = u₁ + u₂ + ... + u_n).

a) Tính u₅; u₆; u₁₅; u₁₆; u₂₀₁₂

b) Tính S₅; S₆; S₁₅; S₁₆; S₂₀₁₂

c) Viết quy trình bấn phím liên tục tính S_n.

Bài 5: (6,0 điểm)

Một người được lĩnh lương khởi điểm là 1,6 triệu đồng một tháng. Cứ ba năm người đó được tăng lương thêm 8%.

a) Hỏi năm làm việc thứ 36 (trước khi về hưu), lương tháng của người đó là bao nhiêu? (làm tròn đến đồng)

b) Hỏi sau 36 năm làm việc người đó được lĩnh tất cả bao nhiêu tiền? (làm tròn đến đồng)

c) Trong năm đầu tiên, cuối mỗi tháng người đó gửi vào ngân hàng một số tiền như nhau với lãi suất 1,4% một tháng. Hai năm tiếp theo, người đó không gửi thêm tiền vào ngân hàng. Hết năm thứ ba, người đó rút cả gốc và lãi được 14 triệu đồng để mua xe máy. Hỏi trong năm đầu tiên, cuối mỗi tháng người đó gửi vào ngân hàng bao nhiêu tiền? (làm tròn đến đồng)

Bài 6: (5,0 điểm)

Cho đa thức f(x) thỏa mãn: f(x) chia cho x + 2 dư 3,589; chia cho x - 3 dư 4,237; chia cho (x + 2)(x - 3) được thương là 2x + 1 và còn dư.

Tính: f(16); f(2); f(12)

Bài 7: (5,0 điểm)

Cho x, y, z là các số không âm thỏa mãn: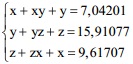

Tính gần đúng (làm tròn đến chữ số thập phân thứ 5) giá trị của biểu thức: E = (x + 1)(y + 1)(z + 1)

Bài 8: (4,0 điểm)

Cho hình thang vuông ABCD (AB // CD, góc A = 90^o) có AB = 2,151 cm; CD = 6,729 cm; AD = 4,736 cm. Tính gần đúng (làm tròn đến phút) góc nhọn tạo bởi hai đường chéo AC, BD.

Bài 9: (6 điểm)

Cho đường tròn tâm O bán kính R. Đặt liên tiếp các dây AB = p ; BC = 2p; CD = q của đường tròn (O; R) ( hình vẽ).

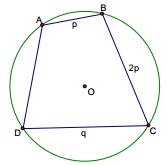
a) Tính gần đúng (làm tròn đến chữ số thập phân thứ 3) độ dài dây AD và diện tích S của tứ giác ABCD với R = 2,156 cm; p = 1,171 cm; q = 3,328 cm.

b) Với R = 2,156 cm. Hãy xác định gần đúng giá trị của p, q (làm tròn đến chữ số thập phân thứ 3) để tứ giác ABCD có diện tích S = 8,356 cm² và góc ABC = 90^o.

Bài 10: (3,0 điểm)

Tìm số tự nhiên n biết

ĐỀ THI MÔN: TOÁN (BẢNG B)

Bài 1: (6 điểm)

a) Tìm giá trị chính xác của biểu thức: A = 123456789²

b) Tính giá trị của biểu thức:

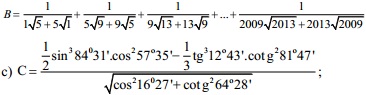
Bài 2: (4 điểm)

Tìm số dư của phép chia:

a) 20122012201220122012 chia cho 2011.

b) chia cho 11

Bài 3: (4 điểm)

Tìm số chữ số của số 2011²⁰¹²

Bài 4: (5 điểm)

Một người vay thế chấp lương của ngân hàng số tiền là 400 triệu đồng. Biết mỗi tháng người đó phải đều đặn trả một số tiền là a và phải chịu lãi suất của số tiền chưa trả là 1,7%/tháng. Biết người đó bắt đầu trả tiền sau 1 tháng và sau 5 năm thì người đó trả hết cả gốc lẫn lãi. Tìm a và tổng số tiền lãi mà người đó phải trả là bao nhiêu? (Đơn vị tiền tệ ngân hàng làm tròn đến đồng).

Bài 5: (5 điểm)

Biết rằng x là một số thực khác 0, tìm giá trị nhỏ nhất của biểu thức:

Bài 6: (6 điểm)

Cho các đường thẳng d₁: 3x – 2y = -16; d₂: 2x + 3y = 11; d₃: 3x + 11y = 10. Gọi A, B, C lần lượt là giao điểm của d₁ và d₂, d₁ và d₃, d₂ và d₃.

a) Tìm toạ độ giao điểm của A, B, C.

b) Tính chu vi tam giác ABC.

c) Tính các góc của tam giác ABC (Đơn vị góc làm tròn đến phút, đơn vị độ dài trên các trục là cm)

Bài 7: (6 điểm)

với n là số tự nhiên khác 0.

a) Tính năm số hạng đầu tiên của dãy.

b) Trình bày cách tìm công thức U_n+2 theo U_n+1 và U_n.

c) Gọi S là tổng từ U₁ đến U_n.Viết quy trình ấn phím tính S_n.

d) Tính S₅, S₁₀.

Bài 8: (5 điểm)

Cho hình chữ nhật ABCD. Qua đỉnh B, vẽ đường vuông góc với đường chéo AC tại H.

a) Biết BH = 17,25 cm; góc BAC = 38^o40'. .Tính diện tích hình chữ nhật ABCD?

b) Tính độ dài đường chéo AC?

Bài 9 (5 điểm)

Cho biết là nghiệm của phương trình ẩn x: x³ + ax² + bx + 16 = 0 (với a, b là các số hữu tỉ). Hãy tìm a, b và các nghiệm còn lại của phương trình.

Bài 10 (4 điểm):

Tìm các số tự nhiên n (1000 < n < 1500) Sao cho cũng là số tự nhiên?

Đáp án đề thi giải toán trên Máy tính cầm tay lớp 9 THCS