Giải Toán 9 bài 2 Căn thức bậc hai và hằng đẳng thức

Giải SGK Toán 9 trang 10, 11, 12

Giải SGK Toán 9 Bài 2: Căn thức bậc hai và hằng đẳng thức

A. Trả lời câu hỏi trang 8 SGK Toán 9 tập 1
B. Giải SGK Toán 9 tập 1 trang 10, 11, 12
C. Giải bài tập toán 9 trang 11, 12 tập 1: Luyện tập

Giải Toán 9 bài 2: Căn thức bậc hai và hằng đẳng thức được VnDoc tổng hợp và đăng tải bao gồm đáp án chi tiết cho các câu hỏi và bài tập trong SGK Toán 9 bài 2 trang 10, 11, 12 giúp các em biết cách trả lời các câu hỏi trong SGK, từ đó vận dụng giải Toán 9 hiệu quả. Sau đây mời các bạn tham khảo chi tiết.

A. Trả lời câu hỏi trang 8 SGK Toán 9 tập 1

Câu hỏi 1 trang 8 SGK Toán 9 tập 1

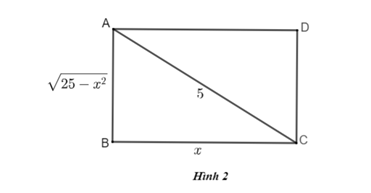
Hình chữ nhật ABCD có đường chéo AC = 5cm và cạnh BC = x (cm) thì cạnh $AB = \sqrt {25 - {x^2}} \left( {cm} \right)$ $AB = \sqrt {25 - {x^2}} \left( {cm} \right)$. Vì sao? (h.2)

Câu hỏi 1 trang 8 SGK Toán 9 tập 1

Hướng dẫn giải:

Áp dụng định lí Pi - ta - go vào tam giác ABC vuông tại B có:

$\eqalign{& A{B^2} + B{C^2} = A{C^2} \Leftrightarrow A{B^2} + {x^2} = {5^2} \cr & \Leftrightarrow A{B^2} = 25 - {x^2} \cr & \Rightarrow AB = \sqrt {\left( {25 - {x^2}} \right)} \,\,\,\left( {do\,\,AB > 0} \right) \cr}$ $\eqalign{& A{B^2} + B{C^2} = A{C^2} \Leftrightarrow A{B^2} + {x^2} = {5^2} \cr & \Leftrightarrow A{B^2} = 25 - {x^2} \cr & \Rightarrow AB = \sqrt {\left( {25 - {x^2}} \right)} \,\,\,\left( {do\,\,AB > 0} \right) \cr}$

Câu hỏi 2 trang 8 SGK Toán 9 tập 1

Với giá trị nào của x thì $\sqrt {5 - 2x}$ $\sqrt {5 - 2x}$ xác định?

Hướng dẫn giải:

Điều kiện để căn thức $\sqrt {5 - 2x}$ $\sqrt {5 - 2x}$ xác định (có nghĩa) là:

$5 - 2x \geqslant 0 \Leftrightarrow 2x \leqslant 5 \Leftrightarrow x \leqslant \frac{5}{2}$ $5 - 2x \geqslant 0 \Leftrightarrow 2x \leqslant 5 \Leftrightarrow x \leqslant \frac{5}{2}$

Câu hỏi 3 trang 8 SGK Toán 9 tập 1

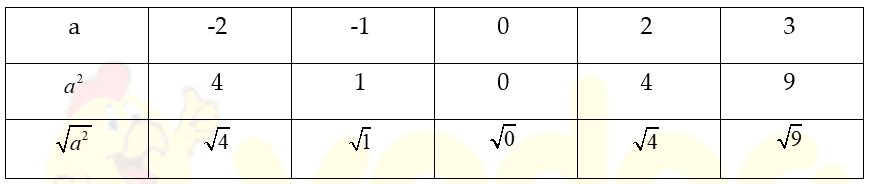
Điền số thích hợp vào ô trống trong bảng sau:

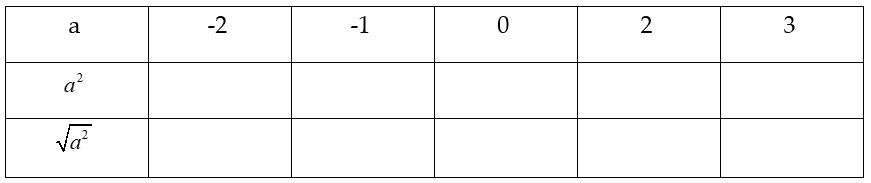
Câu hỏi 3 trang 8 SGK Toán 9 tập 1

Hướng dẫn giải:

Câu hỏi 3 trang 8 SGK Toán 9 tập 1

B. Giải SGK Toán 9 tập 1 trang 10, 11, 12

Bài 6 trang 10 sgk Toán 9 tập 1

Với giá trị nào của a thì mỗi căn thức sau có nghĩa:

$a)\sqrt{\frac{a}{3}},$ $a)\sqrt{\frac{a}{3}},$ $b) \sqrt{-5a};$ $b) \sqrt{-5a};$ $c) \sqrt{4 - a};$ $c) \sqrt{4 - a};$ $d)\sqrt{3a + 7}$ $d)\sqrt{3a + 7}$

Hướng dẫn giải:

a) Ta có: $\sqrt{\frac{a}{3}}$ $\sqrt{\frac{a}{3}}$ có nghĩa khi $\frac{a}{3}\ge0\ \Leftrightarrow\ a\ge0$ $\frac{a}{3}\ge0\ \Leftrightarrow\ a\ge0$

b) Ta có: $\sqrt{-5a}$ $\sqrt{-5a}$ có nghĩa khi $-5a\ge0\ \Leftrightarrow\ a\ \le\frac{0}{-5}\Leftrightarrow\ a\le0$ $-5a\ge0\ \Leftrightarrow\ a\ \le\frac{0}{-5}\Leftrightarrow\ a\le0$

c) Ta có: $\sqrt{4 - a}$ $\sqrt{4 - a}$ có nghĩa khi $4-a\geq 0 \Leftrightarrow -a\geq -4 \Leftrightarrow a\leq 4$ $4-a\geq 0 \Leftrightarrow -a\geq -4 \Leftrightarrow a\leq 4$

d) Ta có: $\sqrt{3a + 7}$ $\sqrt{3a + 7}$ có nghĩa khi $3a+7\geq 0\Leftrightarrow 3a \geq -7 \Leftrightarrow a\geq \frac{-7}{3}$ $3a+7\geq 0\Leftrightarrow 3a \geq -7 \Leftrightarrow a\geq \frac{-7}{3}$

Bài 7 trang 10 SGK Toán 9 tập 1

Tính

$a) \sqrt {{{\left( {0,1} \right)}^2}}$ $a) \sqrt {{{\left( {0,1} \right)}^2}}$ $b) \sqrt {{{\left( { - 0,3} \right)}^2}}$ $b) \sqrt {{{\left( { - 0,3} \right)}^2}}$

$c) - \sqrt {{{\left( { - 1,3} \right)}^2}}$ $c) - \sqrt {{{\left( { - 1,3} \right)}^2}}$ $d) - 0,4\sqrt {{{\left( { - 0,4} \right)}^2}}$ $d) - 0,4\sqrt {{{\left( { - 0,4} \right)}^2}}$

Hướng dẫn giải:

a) Ta có: $\sqrt {{{\left( {0,1} \right)}^2}} = \left| {0,1} \right| = 0,1$ $\sqrt {{{\left( {0,1} \right)}^2}} = \left| {0,1} \right| = 0,1$

b) Ta có: $\sqrt {{{\left( { - 0,3} \right)}^2}} = \left| { - 0,3} \right| = 0,3$ $\sqrt {{{\left( { - 0,3} \right)}^2}} = \left| { - 0,3} \right| = 0,3$

c) Ta có: $- \sqrt {{{\left( { - 1,3} \right)}^2}} = - \left| { - 1,3} \right| = -1,3$ $- \sqrt {{{\left( { - 1,3} \right)}^2}} = - \left| { - 1,3} \right| = -1,3$

d) Ta có:

$- 0,4\sqrt {{{\left( { - 0,4} \right)}^2}} = - 0,4.\left| {-0,4} \right| = - 0,4.0,4$ $- 0,4\sqrt {{{\left( { - 0,4} \right)}^2}} = - 0,4.\left| {-0,4} \right| = - 0,4.0,4$

$= - 0,16$

Bài 8 trang 10 sgk Toán 9 - tập 1

Rút gọn các biểu thức sau:

$a)\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}};$ $a)\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}};$ $b)\sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}}$ $b)\sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}}$

$c)\ 2\sqrt{a^2}$ $c)\ 2\sqrt{a^2}$ với $a\ge0;$ $a\ge0;$ $d)\ 3\sqrt{\left(a-2\right)^2}$ $d)\ 3\sqrt{\left(a-2\right)^2}$ với $a < 2.$

a)

vì $\left\{ \matrix{{2^2} = 4 \hfill \cr {\left( {\sqrt 3 } \right)^2} = 3 \hfill \cr} \right.$ $\left\{ \matrix{{2^2} = 4 \hfill \cr {\left( {\sqrt 3 } \right)^2} = 3 \hfill \cr} \right.$

mà $4>3$ nên $\sqrt{4} > \sqrt{3} \Leftrightarrow 2> \sqrt{3} \Leftrightarrow 2- \sqrt{3}>0.$ $\sqrt{4} > \sqrt{3} \Leftrightarrow 2> \sqrt{3} \Leftrightarrow 2- \sqrt{3}>0.$

$\Leftrightarrow \left| {2 - \sqrt 3 } \right| =2- \sqrt{3}.$ $\Leftrightarrow \left| {2 - \sqrt 3 } \right| =2- \sqrt{3}.$

Do đó: $\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} = \left| {2 - \sqrt 3 } \right|=2- \sqrt{3}$ $\sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} = \left| {2 - \sqrt 3 } \right|=2- \sqrt{3}$

b)

Vì $\left\{ \matrix{{3^2} = 9 \hfill \cr {\left( {\sqrt {11} } \right)^2} = 11 \hfill \cr} \right.$ $\left\{ \matrix{{3^2} = 9 \hfill \cr {\left( {\sqrt {11} } \right)^2} = 11 \hfill \cr} \right.$

mà $9<11$ nên $\sqrt{9} < \sqrt{11} \Leftrightarrow 3< \sqrt{11} \Leftrightarrow 3- \sqrt{11} <0$ $\sqrt{9} < \sqrt{11} \Leftrightarrow 3< \sqrt{11} \Leftrightarrow 3- \sqrt{11} <0$

$\Leftrightarrow \left| {3 - \sqrt {11} } \right| =-(3- \sqrt{11})=-3+\sqrt{11}$ $\Leftrightarrow \left| {3 - \sqrt {11} } \right| =-(3- \sqrt{11})=-3+\sqrt{11}$

$=\sqrt{11}-3.$ $=\sqrt{11}-3.$

Do đó: $\sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}} = \left| {3 - \sqrt {11} } \right| =\sqrt{11}-3.$ $\sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}} = \left| {3 - \sqrt {11} } \right| =\sqrt{11}-3.$

c) Ta có: $2\sqrt {{a^2}} = 2\left| a \right| = 2{\rm{a}}$ $2\sqrt {{a^2}} = 2\left| a \right| = 2{\rm{a}}$ (vì $a \ge 0$ $a \ge 0$ )

d) Vì $a < 2$ nên $a - 2<0$.

$\Leftrightarrow \left| a-2 \right|=-(a-2)=-a+2=2-a$ $\Leftrightarrow \left| a-2 \right|=-(a-2)=-a+2=2-a$

Do đó: $3\sqrt {{{\left( {a - 2} \right)}^2}} = 3\left| {a - 2} \right| = 3\left( {2 - a} \right)$ $3\sqrt {{{\left( {a - 2} \right)}^2}} = 3\left| {a - 2} \right| = 3\left( {2 - a} \right)$

$= 6 - 3a.$

Bài 9 trang 11 sgk Toán 9 - tập 1

Tìm x biết

a) $\sqrt{x^2}=7$ $\sqrt{x^2}=7$

b) $\sqrt{x^2}= \left | -8 \right |$ $\sqrt{x^2}= \left | -8 \right |$

c) $\sqrt{4^2}=7$ $\sqrt{4^2}=7$

d) $\sqrt{9x^2}= \left |-12 \right |$ $\sqrt{9x^2}= \left |-12 \right |$

Hướng dẫn giải:

a)

$\sqrt{7^2}=7$ $\sqrt{7^2}=7$

$\Leftrightarrow \left |x \right | =7$ $\Leftrightarrow \left |x \right | =7$

$\Leftrightarrow x=\pm 7$ $\Leftrightarrow x=\pm 7$

b)

$\sqrt{x^2}= \left |-8 \right |$ $\sqrt{x^2}= \left |-8 \right |$

$\Leftrightarrow \left | x \right | =8$ $\Leftrightarrow \left | x \right | =8$

$x=\pm 8$ $x=\pm 8$

c)

$\sqrt{4x^2}=6$ $\sqrt{4x^2}=6$

$\Leftrightarrow\sqrt{2x^2}=6$ $\Leftrightarrow\sqrt{2x^2}=6$

$\Leftrightarrow \left |2x \right | =6$ $\Leftrightarrow \left |2x \right | =6$

$\Leftrightarrow 2x=\pm 6$ $\Leftrightarrow 2x=\pm 6$

$\Leftrightarrow =\pm 3$ $\Leftrightarrow =\pm 3$

d)

$\sqrt{9x^2} = \left |-12 \right |$ $\sqrt{9x^2} = \left |-12 \right |$

$\Leftrightarrow\sqrt{3x^2}=12$ $\Leftrightarrow\sqrt{3x^2}=12$

$\Leftrightarrow \left |3x \right | =12$ $\Leftrightarrow \left |3x \right | =12$

$\Leftrightarrow3x=\pm12$ $\Leftrightarrow3x=\pm12$

$\Leftrightarrow x=\pm 4$ $\Leftrightarrow x=\pm 4$

Bài 10 trang 11 sgk Toán 9 - tập 1

Chứng minh

a) $(\sqrt{3}- 1)^{2}= 4 - 2\sqrt{3};$ $(\sqrt{3}- 1)^{2}= 4 - 2\sqrt{3};$

b) $\sqrt{4 - 2\sqrt{3}}- \sqrt{3} = -1$ $\sqrt{4 - 2\sqrt{3}}- \sqrt{3} = -1$

Hướng dẫn giải:

a) Ta có: $VT={\left( {\sqrt 3 - 1} \right)^2} = {\left( {\sqrt 3 } \right)^2} - 2. \sqrt 3 .1 + {1^2}$ $VT={\left( {\sqrt 3 - 1} \right)^2} = {\left( {\sqrt 3 } \right)^2} - 2. \sqrt 3 .1 + {1^2}$

$= 3 - 2\sqrt 3 + 1$ $= 3 - 2\sqrt 3 + 1$

$=(3+1)-2\sqrt 3$ $=(3+1)-2\sqrt 3$

$= 4 - 2\sqrt 3 = VP$ $= 4 - 2\sqrt 3 = VP$

Vậy $(\sqrt{3}-1)^2=4-2\sqrt{3}(đpcm)$ $(\sqrt{3}-1)^2=4-2\sqrt{3}(đpcm)$

b) Ta có:

VT = $\sqrt {4 - 2\sqrt 3 } - \sqrt 3 = \sqrt {\left( {3 + 1} \right) - 2\sqrt 3 } - \sqrt 3$ $\sqrt {4 - 2\sqrt 3 } - \sqrt 3 = \sqrt {\left( {3 + 1} \right) - 2\sqrt 3 } - \sqrt 3$

$= \sqrt {3 - 2\sqrt 3 + 1} - \sqrt 3$ $= \sqrt {3 - 2\sqrt 3 + 1} - \sqrt 3$

$= \sqrt {{{\left( {\sqrt 3 } \right)}^2} - 2.\sqrt 3 .1 + {1^2}} - \sqrt 3$ $= \sqrt {{{\left( {\sqrt 3 } \right)}^2} - 2.\sqrt 3 .1 + {1^2}} - \sqrt 3$

$= \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} - \sqrt 3$ $= \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} - \sqrt 3$

$= \left| {\sqrt 3 - 1} \right| - \sqrt 3.$ $= \left| {\sqrt 3 - 1} \right| - \sqrt 3.$

Lại có:

$\left\{ \matrix{ {\left( {\sqrt 3 } \right)^2} = 3 \hfill \cr {\left( {\sqrt 1 } \right)^2} = 1 \hfill \cr} \right.$ $\left\{ \matrix{ {\left( {\sqrt 3 } \right)^2} = 3 \hfill \cr {\left( {\sqrt 1 } \right)^2} = 1 \hfill \cr} \right.$

Mà $3>1 \Leftrightarrow \sqrt 3 > \sqrt 1 \Leftrightarrow \sqrt 3 > 1 \Leftrightarrow \sqrt 3 -1 > 0.$ $3>1 \Leftrightarrow \sqrt 3 > \sqrt 1 \Leftrightarrow \sqrt 3 > 1 \Leftrightarrow \sqrt 3 -1 > 0.$

$\Rightarrow \left| \sqrt 3 -1 \right| = \sqrt 3 -1.$ $\Rightarrow \left| \sqrt 3 -1 \right| = \sqrt 3 -1.$

Do đó $\left| {\sqrt 3 - 1} \right| - \sqrt 3 = \sqrt 3 -1 - \sqrt 3$ $\left| {\sqrt 3 - 1} \right| - \sqrt 3 = \sqrt 3 -1 - \sqrt 3$

$= (\sqrt 3 - \sqrt 3) -1= -1 = VP.$ $= (\sqrt 3 - \sqrt 3) -1= -1 = VP.$

Vậy $\sqrt {4 - 2\sqrt 3 } - \sqrt 3 =-1 (đpcm)$ $\sqrt {4 - 2\sqrt 3 } - \sqrt 3 =-1 (đpcm)$

C. Giải bài tập toán 9 trang 11, 12 tập 1: Luyện tập

Bài 11 trang 11 sgk Toán 9 tập 1

Tính

a) $\sqrt{16}.\sqrt{25}+\sqrt{196}:\sqrt{49}$ $\sqrt{16}.\sqrt{25}+\sqrt{196}:\sqrt{49}$

b) $36:\sqrt{2.3^2.18}-\sqrt{169}$ $36:\sqrt{2.3^2.18}-\sqrt{169}$

c) $\sqrt{\sqrt{81}}$ $\sqrt{\sqrt{81}}$

d) $\sqrt{3^2+4^2}$ $\sqrt{3^2+4^2}$

Hướng dẫn giải:

a) Ta có: $\sqrt{16}.\sqrt{25}+\sqrt{196}:\sqrt{49}$ $\sqrt{16}.\sqrt{25}+\sqrt{196}:\sqrt{49}$

$=\sqrt{4^2}.\sqrt{5^2}+\sqrt{14^2}:\sqrt{7^2}$ $=\sqrt{4^2}.\sqrt{5^2}+\sqrt{14^2}:\sqrt{7^2}$

$=4.5+14:7$

$=20+2=22.$

b) Ta có:

$36:\sqrt{2.3^2.18}-\sqrt{169}=36:\sqrt{(2.3^2).18}-\sqrt{13^2}$ $36:\sqrt{2.3^2.18}-\sqrt{169}=36:\sqrt{(2.3^2).18}-\sqrt{13^2}$

$=36:\sqrt{(2.9).18}-\left|13\right|$ $=36:\sqrt{(2.9).18}-\left|13\right|$

$=36:\sqrt{18.18}-13$ $=36:\sqrt{18.18}-13$

$=36:\sqrt{18^2}-13$ $=36:\sqrt{18^2}-13$

$=36:\left|18\right|-13$ $=36:\left|18\right|-13$

$=36:18−13$

$=2−13=−1$

c) Ta có: $\sqrt{81}=\sqrt{9^2}=\left|9\right|=9$ $\sqrt{81}=\sqrt{9^2}=\left|9\right|=9$

$\Rightarrow\sqrt{\sqrt{81}}=\sqrt{9}=\sqrt{3^2}=\left|3\right|=3$ $\Rightarrow\sqrt{\sqrt{81}}=\sqrt{9}=\sqrt{3^2}=\left|3\right|=3$

d) Ta có: $\sqrt{3^2+4^2}=\sqrt{16+9}=\sqrt{25}=\sqrt{5^2}=\left|5\right|=5$ $\sqrt{3^2+4^2}=\sqrt{16+9}=\sqrt{25}=\sqrt{5^2}=\left|5\right|=5$

Bài 12 trang 11 sgk Toán 9 tập 1

Tìm x để mỗi căn thức sau có nghĩa:

a) $\sqrt{2x+7};$ $\sqrt{2x+7};$ c) $\sqrt{\frac{1}{-1+x}}$ $\sqrt{\frac{1}{-1+x}}$

b) $\sqrt{-3x+4};$ $\sqrt{-3x+4};$ d) $\sqrt{1+x^2}$ $\sqrt{1+x^2}$

Hướng dẫn giải:

a) Ta có:

$\sqrt{2x+7}$ $\sqrt{2x+7}$ có nghĩa khi và chỉ khi: $2x+7\ge0$ $2x+7\ge0$

$\Leftrightarrow2x\ge-7$ $\Leftrightarrow2x\ge-7$

$\Leftrightarrow\ x\ \ge\ \frac{-7}{2}.$ $\Leftrightarrow\ x\ \ge\ \frac{-7}{2}.$

b) Ta có

$\sqrt{-3x+4}$ $\sqrt{-3x+4}$ có nghĩa khi và chỉ khi: $−3x+4\ge0$ $−3x+4\ge0$

$\Leftrightarrow-3x\ge-4$ $\Leftrightarrow-3x\ge-4$

$\Leftrightarrow\ x\le\frac{-4}{-3}$ $\Leftrightarrow\ x\le\frac{-4}{-3}$

$\Leftrightarrow\ x\le\frac{4}{3}$ $\Leftrightarrow\ x\le\frac{4}{3}$

c) Ta có:

$\sqrt{\frac{1}{-1+x}}$ $\sqrt{\frac{1}{-1+x}}$ có nghĩa khi và chỉ khi:

$\left\{ \matrix{{1 \over { - 1 + x}} \ge 0 \hfill \cr - 1 + x \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{- 1 + x \ge 0 \hfill \cr - 1 + x \ne 0 \hfill \cr} \right. \Leftrightarrow - 1 + x > 0$ $\left\{ \matrix{{1 \over { - 1 + x}} \ge 0 \hfill \cr - 1 + x \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{- 1 + x \ge 0 \hfill \cr - 1 + x \ne 0 \hfill \cr} \right. \Leftrightarrow - 1 + x > 0$

$\Leftrightarrow x > 1$ $\Leftrightarrow x > 1$

d) $\sqrt{1 + x^{2}}$ $\sqrt{1 + x^{2}}$

Ta có: $x^2\geq 0$ $x^2\geq 0$, với mọi số thực $x$

$\Leftrightarrow x^2+1 \geq 0+ 1$ $\Leftrightarrow x^2+1 \geq 0+ 1$, (Cộng cả 2 vế của bất đẳng thức trên với $1$)

$\Leftrightarrow x^2+1 \geq 1$ $\Leftrightarrow x^2+1 \geq 1$, mà $1 >0$

$\Leftrightarrow x^2+1 >0$ $\Leftrightarrow x^2+1 >0$

Vậy căn thức trên luôn có nghĩa với mọi số thực $x$

Bài 13 trang 11 sgk Toán 9 tập 1

Rút gọn các biểu thức sau:

a) $2\sqrt {{a^2}} - 5a$ $2\sqrt {{a^2}} - 5a$ với $(a<0)$.

b) $\sqrt{25a^{2}}+ 3a$ $\sqrt{25a^{2}}+ 3a$ với $(a\ge0)$ $(a\ge0)$.

c) $\sqrt {9{a^4}} + 3{a^2}$ $\sqrt {9{a^4}} + 3{a^2}$,

d) $5\sqrt{4a^{6}} - 3a^{3}$ $5\sqrt{4a^{6}} - 3a^{3}$với $a<0$

a) Ta có: $2\sqrt{a^2}-5a=2|a|-5a$ $2\sqrt{a^2}-5a=2|a|-5a$

$=2.(-a)-5a$ (Vì $a<0$ nên $\left| a \right| =-a$ $\left| a \right| =-a$)

$=-2a-5a$

$=(-2-5)a$

$=-7a$

Vậy $2 \sqrt{a^2}-5a=-7a$ $2 \sqrt{a^2}-5a=-7a$.

b) Ta có: $\sqrt{9a^{4}}+3a^2=\sqrt {9}. \sqrt{a^4}+ 3a^2$ $\sqrt{9a^{4}}+3a^2=\sqrt {9}. \sqrt{a^4}+ 3a^2$

$=\sqrt{3^2}.\sqrt{(a^2)^2}+3a^2$ $=\sqrt{3^2}.\sqrt{(a^2)^2}+3a^2$

$=3a^2 + 3a^2$

$=(3+3)a^2$

$=6a^2.$

(Vì $a^2\geq 0,\ \forall\,\, a\,\,\epsilon \,\,\mathbb{R}\Rightarrow |a^2|=a^2$ $a^2\geq 0,\ \forall\,\, a\,\,\epsilon \,\,\mathbb{R}\Rightarrow |a^2|=a^2$).

c) Ta có: $\sqrt{25a^{2}} + 3a=\sqrt{25}. \sqrt{a^2}+3a$ $\sqrt{25a^{2}} + 3a=\sqrt{25}. \sqrt{a^2}+3a$

$=\sqrt{5^2}. \left| a \right| +3a$ $=\sqrt{5^2}. \left| a \right| +3a$

$=5a+3a$

$=(5+3)a$

$=8a.$

d) Ta có:

$5\sqrt{4a^{6}} - 3a^3=5.\sqrt{4}.\sqrt{a^6} -3a^3$ $5\sqrt{4a^{6}} - 3a^3=5.\sqrt{4}.\sqrt{a^6} -3a^3$

$=5.\sqrt{2^2}.\sqrt{(a^3)^2}-3a^3$ $=5.\sqrt{2^2}.\sqrt{(a^3)^2}-3a^3$

$=5.2.(-a^3)-3a^3 ,$ (vì $a<0$ $|a^3|=-a^3$)

$=10.(-a^3) - 3a^3$

$=-10a^3-3a^3$

$=(-10-3)a^3$

$=-13a^3.$

Bài 14 trang 11 sgk Toán 9 tập 1

Phân tích thành nhân tử:

$a) x^{2}- 3.$ $a) x^{2}- 3.$ $b) x^{2}- 6;$ $b) x^{2}- 6;$

$c) x^{2} + 2\sqrt{3}x + 3;$ $c) x^{2} + 2\sqrt{3}x + 3;$ $d) x^{2} - 2\sqrt{5}x + 5.$ $d) x^{2} - 2\sqrt{5}x + 5.$

Hướng dẫn giải:

a) Ta có:

$x^{2} - 3=x^2-(\sqrt{3})^2$ $x^{2} - 3=x^2-(\sqrt{3})^2$

$=(x-\sqrt{3})(x+\sqrt{3})$ $=(x-\sqrt{3})(x+\sqrt{3})$ (Áp dụng hằng đẳng thức số 3)

b) Ta có:

$x^{2}- 6=x^2-(\sqrt{6})^2$ $x^{2}- 6=x^2-(\sqrt{6})^2$

$=(x-\sqrt{6})(x+\sqrt{6})$ $=(x-\sqrt{6})(x+\sqrt{6})$ (Áp dụng hằng đẳng thức số 3)

c) Ta có:

$x^2+2\sqrt{3}x + 3=x^2+2.x.\sqrt{3}+(\sqrt{3})^2$ $x^2+2\sqrt{3}x + 3=x^2+2.x.\sqrt{3}+(\sqrt{3})^2$

$=(x+\sqrt{3})^2$ $=(x+\sqrt{3})^2$ (Áp dụng hằng đẳng thức số 1)

d) Ta có:

$x^2-2\sqrt{5}x+5=x^2-2.x.\sqrt{5}+(\sqrt{5})^2$ $x^2-2\sqrt{5}x+5=x^2-2.x.\sqrt{5}+(\sqrt{5})^2$

$=(x-\sqrt{5})^2$ $=(x-\sqrt{5})^2$ (Áp dụng hằng đẳng thức số 2).

Bài 15 trang 11 sgk Toán 9 tập 1

Giải các phương trình sau:

$a) {x^2} - 5 = 0;$ $a) {x^2} - 5 = 0;$ $b) {x^2} - 2\sqrt {11} x + 11 = 0$ $b) {x^2} - 2\sqrt {11} x + 11 = 0$

Hướng dẫn giải:

a) Ta có: ${x^2} - 5 = 0$ ${x^2} - 5 = 0$

$\Leftrightarrow {x^2} - {\left( {\sqrt 5 } \right)^2} = 0$ $\Leftrightarrow {x^2} - {\left( {\sqrt 5 } \right)^2} = 0$ (AD hằng đẳng thức số 3)

$\Leftrightarrow \left( {x + \sqrt 5 } \right).\left( {x - \sqrt 5 } \right) = 0$ $\Leftrightarrow \left( {x + \sqrt 5 } \right).\left( {x - \sqrt 5 } \right) = 0$

$\Leftrightarrow \left[ \matrix{ x + \sqrt 5 = 0 \hfill \cr x - \sqrt 5 = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = - \sqrt 5 \hfill \cr x = \sqrt 5 \hfill \cr} \right.$ $\Leftrightarrow \left[ \matrix{ x + \sqrt 5 = 0 \hfill \cr x - \sqrt 5 = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = - \sqrt 5 \hfill \cr x = \sqrt 5 \hfill \cr} \right.$

Vậy $S = \left\{ { - \sqrt 5 ;\sqrt 5 } \right\}$ $S = \left\{ { - \sqrt 5 ;\sqrt 5 } \right\}$.

b) Ta có:

${x^2} - 2\sqrt {11} x + 11 = 0$ ${x^2} - 2\sqrt {11} x + 11 = 0$
$\Leftrightarrow {x^2} - 2.x.\sqrt {11} + {\left( {\sqrt {11} } \right)^2} = 0$ $\Leftrightarrow {x^2} - 2.x.\sqrt {11} + {\left( {\sqrt {11} } \right)^2} = 0$
$\Leftrightarrow {\left( {x - \sqrt {11} } \right)^2} = 0$ $\Leftrightarrow {\left( {x - \sqrt {11} } \right)^2} = 0$
$\Leftrightarrow x - \sqrt {11} =0$ $\Leftrightarrow x - \sqrt {11} =0$

$\Leftrightarrow x = \sqrt {11}$ $\Leftrightarrow x = \sqrt {11}$

Vậy $S = \left\{ {\sqrt {11} } \right\}$ $S = \left\{ {\sqrt {11} } \right\}$

Bài 16 trang 12 sgk Toán 9 tập 1

Đố Hãy tìm chỗ sai trong phép chứng minh "Con muỗi nặng bằng con voi" dưới đây.

Căn thức bậc hai và hằng đẳng thức

Giả sử con muỗi nặng m (gam), còn con voi nặng V (gam). Ta có

$m^2+V^2=V^2+m^2$

Cộng hai về với $-2mV$. Ta có

$m^2-2mV+V^2=V^2-2mV+m^2,$

hay $\left(m-V\right)^2=\left(V-m\right)^2$ $\left(m-V\right)^2=\left(V-m\right)^2$

Lấy căn bậc hai mỗi vế của bất đẳng thức trên, ta được:

$\sqrt{\left(m-V\right)^2}=\sqrt{\left(V-m\right)^2}$ $\sqrt{\left(m-V\right)^2}=\sqrt{\left(V-m\right)^2}$

Do đó $m-V=V-m$

Từ đó ta có $2m=2V$, suy ra $m=V$. Vậy con muỗi nặng bằng con voi (!).

Hướng dẫn giải:

Phép chứng minh sai ở chỗ: Sau khi lấy căn bậc hai mỗi vế của đẳng thức

$(m−V)^2=(V−m)^2$

Ta được kết quả $│m-V│=│V-m│$ chứ không thể có $m-V=V-m.$

.......................

Bài tiếp theo: Giải Toán 9 bài 3: Liên hệ giữa phép nhân và phép khai phương

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 9. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Câu hỏi trong bài