Giải Toán 9 bài 7: Phương trình quy về phương trình bậc hai
Giải Toán 9 bài 7 tập 2: Phương trình quy về phương trình bậc hai
Giải bài tập Toán 9 bài 7: Phương trình quy về phương trình bậc hai tổng hợp câu hỏi và đáp án cho các câu hỏi trong SGK Toán 9 bài 7, giúp các em dễ dàng trả lời câu hỏi trong bài. Đây là tài liệu tham khảo hữu ích dành cho thầy cô trong quá trình giảng dạy, ôn luyện kiến thức đã học cho các bạn đồng thời cũng giúp học sinh học tốt môn Toán lớp 9. Mời các bạn tham khảo chi tiết sau đây.
Trả lời câu hỏi Toán 9 Tập 2 Bài 7 trang 55: Giải các phương trình trùng phương:
a) 
\(4x^4+x^2-5=0\);
b) \(3x^4+4x^2+1=0\).
Lời giải
a) \(4x^2+x^2-5=0\);
Đặt x2 = t (t ≥ 0). Phương trình trở thành:
4t2 + t - 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
\(t_1=1;t_2=\frac{-5}{4}\)
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x2 = 1 ⇔ x = ±1
Vậy phương trình có 2 nghiệm x1 = 1; x2 = -1
b) 3x4 + 4x2 + 1 = 0
Đặt x2 = t (t ≥ 0). Phương trình trở thành:
\(3t^2+4t+1=0\)
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
\(t_1=-1;t_2=\frac{-1}{3}\)
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.
Trả lời câu hỏi Toán 9 Tập 2 Bài 7 trang 55: Giải phương trình
Bằng cách điền vào các chỗ trống (…) và trả lời các câu hỏi.
- Điều kiện: x ≠ …
- Khử mẫu và biến đổi, ta được: \(x^2-3x+6=\dots⇔x^2-4x+3=0.\)
- Nghiệm của phương trình \(x^2-4x+3=0\) là \(x_1=\dots;x_2=\dots\)
Hỏi x có thỏa mãn điều kiện nói trên không? Tương tự, đối với x2?
Vậy nghiệm của phương trình đã cho là:....
Lời giải
- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: \(x^2-3x+6=x+3⇔x^2-4x+3=0.\)
- Nghiệm của phương trình x2 – 4x + 3 = 0 là: x1 = 1; x2 = 3
x1 có thỏa mãn điều kiện nói trên
x2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1
Trả lời câu hỏi Toán 9 Tập 2 Bài 7 trang 56: Giải phương trình sau bằng cách đưa về phương trình tích: \(x^3+3x^2+2x=0\).
Lời giải
\(x^3+3x^2+2x=0⇔x(x^2+3x+2)=0\)
⇔ x = 0 hoặc \(x^2+3x+2=0(1)\)
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2
Bài 34 (trang 56 SGK Toán 9 tập 2): Giải các phương trình trùng phương:
a) \(x^4-5x^2+4=0\);
b) 2x4 – 3x2 – 2 = 0;
c) 3x4 + 10x2 + 3 = 0
Lời giải
a) x4 – 5x2 + 4 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành: \(t^2-5t+4=0\)\(t^2-5t+4=0\left(2\right)\)
Giải (2): Có \(a=1;b=-5;c=4⇒a+b+c=0\)
⇒ Phương trình có hai nghiệm \(t_1=1;t_2=\frac{c}{a}=4\)
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) \(2x^4-3x^2-2=0;(1)\)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành: \(2t^2-3t-2=0(2)\)
Giải (2): Có \(a=2;b=-3;c=-2\)
\(⇒Δ=(-3)^2-4.2.(-2)=25>0\)
⇒ Phương trình có hai nghiệm
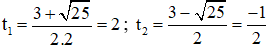
Chỉ có giá trị t1 = 2 thỏa mãn điều kiện.
+ Với \(t=2⇒x^2=2⇒x=\sqrt{2}\) hoặc \(x=-\sqrt{2}\);
Vậy phương trình (1) có tập nghiệm \(S=-\sqrt{2};\sqrt{2}\).
c) \(3x^4+10x^2+3=0(1)\)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành: \(3t^2+10t+3=0(2)\)
Giải (2): Có \(a=3;b=10;c=3\)
\(⇒Δ’=5^2-3.3=16>0\)
⇒ Phương trình có hai nghiệm phân biệt
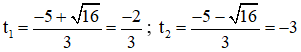
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Bài 35 (trang 56 SGK Toán 9 tập 2): Giải các phương trình:
\(a) \dfrac{(x+ 3)(x-3)}{3}+ 2 = x(1 - x)\)
\(b) \dfrac{x+ 2}{x-5} + 3 = \dfrac{6}{2-x}\)
\(a) \dfrac{(x+ 3)(x-3)}{3}+ 2 = x(1 - x)\)
Quy đồng và khử mẫu ta được:
\(\Leftrightarrow {x^2} - 9 + 6 = 3x{\rm{ - }}3{x^2}\)
\(\Leftrightarrow 4{x^2}{\rm{ - }}3x{\rm{ - }}3 = 0;\Delta = 57>0\)
Vậy phương trình đã cho có 2 nghiệm phân biệt là:
\(\displaystyle {x_1} = {\rm{ }}{{3 + \sqrt {57} } \over 8},{x_2} = {\rm{ }}{{3 - \sqrt {57} } \over 8}\)
\(b) \dfrac{x+ 2}{x-5} + 3 = \dfrac{6}{2-x}\)
Điều kiện x ≠ 2, x ≠ 5.
Quy đồng và khử mẫu ta được:
(x + 2)(2 – x) + 3(x – 5)(2 – x) = 6(x – 5)
\(\Leftrightarrow 4 - {x^2} + 3\left( {2x - {x^2} - 10 + 5x} \right) = 6x - 30\)
\(\Leftrightarrow 4{\rm{ - }}{x^2}{\rm{ - }}3{x^2} + 21x{\rm{ - }}30 = 6x{\rm{ - }}30\)
\(\Leftrightarrow 4{x^2}{\rm{ - }}15x{\rm{ - }}4 = 0,\)
\(\Delta = 225 + 64 = 289 > 0,\sqrt \Delta = 17\)
Khi đó phương trình đã cho có 2 nghiệm là \(\displaystyle {x_1} = {\rm{ }} - {1 \over 4},{x_2} = 4\) (thỏa mãn điều kiện)
Bài 36 (trang 56 SGK Toán 9 tập 2): Giải các phương trình:
a) \((3x^2-5x+1)(x^2-4)=0\);
b) \((2x^2+x-4)^2-(2x-1)^2=0\).
Lời giải
a) \((3x^2-5x+1)(x^2-4)=0\)
\(⇔3x^2-5x+1=0(1)\)
hoặc \(x^2-4=0(2)\)
+ Giải (1): \(3x^2-5x+1=0\)
Có \(a=3;b=-5;c=1⇒Δ=(-5)^2-4.3=13>0\)
Phương trình có hai nghiệm: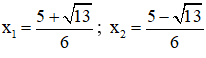 
+ Giải (2): \(x^2-4=0⇔x^2=4⇔x=2\) hoặc x = -2.
Vậy phương trình có tập nghiệm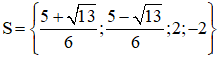 
b) \((2x^2+x-4)^2-(2x-1)^2=0\)
\(⇔(2x^2+x-4-2x+1)(2x^2+x-4+2x-1)=0\)
\(⇔(2x^2-x-3)(2x^2+3x-5)=0\)
\(⇔2x^2-x-3=0(1)\)
hoặc \(2x^2+3x-5=0(2)\)
+ Giải \((1):2x^2-x-3=0\)
Có \(a=2;b=-1;c=-3⇒a-b+c=0\)
⇒ Phương trình có hai nghiệm x = -1 và \(x=\frac{-c}{a}=\frac{3}{2}\).
+ Giải (2): \(2x^2+3x-5=0\)
Có \(a=2;b=3;c=-5⇒a+b+c=0\)
⇒ Phương trình có hai nghiệm x = 1 và \(x=\frac{c}{a}=\frac{-5}{2}\).
Vậy phương trình có tập nghiệm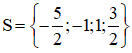 
Luyện tập (trang 56-57)
Bài 37 (trang 56 SGK Toán 9 tập 2): Giải phương trình trùng phương:
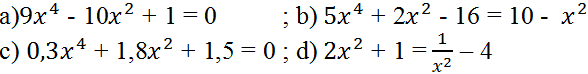
Lời giải
a) \(9x^4-10x^2+1=0(1)\)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành: \(9t^2-10t+1=0(2)\)
Giải (2):
Có a = 9; b = -10; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm \(t_1=1;t_2=\frac{c}{a}=\frac{1}{9}\).
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1.
Vậy phương trình (1) có tập nghiệm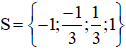 
b) \(5x^4+2x^2-16=10-x^2\)
\(⇔5x^4+2x^2-16-10+x^2=0\)
\(⇔5x^4+3x^2-26=0(1)\)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành: \(5t^2+3t-26=0(2)\)
Giải (2):
Có \(a=5;b=3;c=-26\)
\(⇒Δ=3^2-4.5.(-26)=529>0\)
⇒ Phương trình có hai nghiệm phân biệt
Đối chiếu điều kiện chỉ có t1 = 2 thỏa mãn
+ Với \(t=2⇒x^2=2⇒x=\sqrt{2}\) hoặc \(x=-\sqrt{2}\).
Vậy phương trình (1) có tập nghiệm \(S=-\sqrt{2};\sqrt{2}\)
c) \(0,3x^4+1,8x^2+1,5=0(1)\)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó, (1) trở thành: \(0,3t^2+1,8t+1,5=0(2)\)
Giải (2):
có \(a=0,3;b=1,8;c=1,5\)
\(⇒a-b+c=0\)
⇒ Phương trình có hai nghiệm t1 = -1 và \(t_2=\frac{-c}{a}=-5\).
Cả hai nghiệm đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
\(2x^4+x^2=1-4^2\)
\(⇔2x^4+x^2+4x^2-1=0\)
⇔ 2x4 + 5x2 – 1 = 0 (1)
Đặt t = x2, điều kiện t > 0.
Khi đó (1) trở thành: \(2t^2+5t-1=0(2)\)
Giải (2):
Có \(a=2;b=;c=-1\)
\(⇒Δ=5^2-4.2.(-1)=33>0\)
⇒ Phương trình có hai nghiệm phân biệt:
Đối chiếu với điều kiện thấy có nghiệm t1 thỏa mãn.
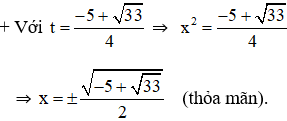
Vậy phương trình có tập nghiệm 
Bài 38 (trang 56-57 SGK Toán 9 tập 2): Giải các phương trình:
Lời giải
a) \((x-3)^2+(x+4)^2=23-3x\)
\(⇔x^2-6x+9+x^2+8x+16=23-3x\)\(⇔x^2-6x+9+x^2+8x+16+3x-23=0\)
\(⇔2x^2+5x+2=0\)
Có \(a=2;b=5;c=2⇒Δ=5^2-4.2.2=9>0\)
⇒ Phương trình có hai nghiệm:
Vậy phương trình có tập nghiệm 
b) \(x^3+2x^2-(x-3)^2=(x-1)(x^2-2)\)
\(⇔x^3+2x^2-(x^2-6x+9)=x^3-x^2-2x+2\)
\(⇔x^3+2x^2-x^2+6x-9-x^3+x^2+2x-2=0\)
\(⇔2x^2+8x-11=0.\)
Có \(a=2;b=8;c=-11⇒Δ’=4^2-2.(-11)=38>0\)
⇒ Phương trình có hai nghiệm:
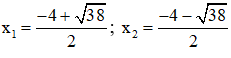
Vậy phương trình có tập nghiệm 
c) \((x-1)^3+0,5x^2=x(x^2+1,5)\)
\(⇔x^3-3x^2+3x-1+0,5x^2=x^3+1,5x\)
\(⇔x^3+1,5x-x^3+3x^2-3x+1-0,5x^2=0\)
\(⇔2,5x^2-1,5x+1=0\)
Có \(a=2,5;b=-1,5;c=1\)
\(⇒Δ=(-1,5)^2-4.2,5.1=-7,75<0\)
Vậy phương trình vô nghiệm.
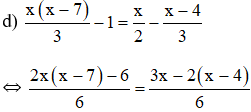
\(⇔2x(x-7)-6=3x-2(x-4)\)
\(⇔2x^2-14x-6=3x-2x+8\)
\(⇔2x^2-14x-6-3x+2x-8=0\)
\(⇔2x^2-15x-14=0.\)
Có \(a=2;b=-15;c=-14\)
\(⇒Δ=(-15)^2-4.2.(-14)=337>0\)
⇒ Phương trình có hai nghiệm:
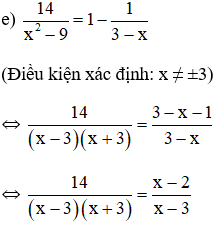
\(⇔14=(x-2)(x+3)\)
\(⇔14=x^2-2x+3x-6\)
\(⇔x^2+x-20=0\)
Có \(a=1;b=1;c=-20\)
\(⇒Δ=1^2-4.1.(-20)=81>0\)
Phương trình có hai nghiệm:
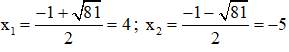
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm S = {-5; 4}.
Bài 39 (trang 57 SGK Toán 9 tập 2): Giải phương trình bằng cách đưa về phương trình tích:
a)\((3x^2-7x-10).[2x^2+(1-5)x+5-3]=0\)
b) \(x^3+3x^2-2x-6=0\);
c) \((x^2-1)(0,6x+1)=0,6x^2+x;\)
d) \((x^2+2x-5)^2=(x^2-x+5)^2\).
Lời giải
a)\((3x^2-7x-10).[2x^2+(1-5)x+5-3]=0\)
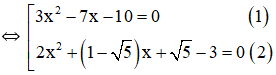
+ Giải (1):
\(3x^2-7x-10=0\)
Có \(a=3;b=-7;c=-10\)
\(⇒a-b+c=0\)
⇒ (1) có hai nghiệm x1 = -1 và \(x^2=\frac{-c}{a}=\frac{10}{3}\).
+ Giải (2):
\(2x^2+(1-\sqrt{5})x+\sqrt{5}-3=0\)
Có \(a=2;b=1-\sqrt{5};c=\sqrt{5}-3\)
\(⇒a+b+c=0\)
⇒ (2) có hai nghiệm:
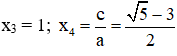
Vậy phương trình có tập nghiệm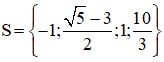 
b) \(x^3+3x^2-2x-6=0\)
\(⇔(x^2+3x^2)-(2x+6)=0\)
\(⇔x^2(x+3)-2(x+3)=0\)
\(⇔(x^2-2)(x+3)=0\)
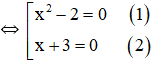
+ Giải (1): \(x^2-2=0⇔x^2=2⇔x=\sqrt{2}\) hoặc \(x=-\sqrt{2}.\)
+ Giải (2): \(x+3=0⇔x=-3\).
Vậy phương trình có tập nghiệm \(S=-3;-\sqrt{2};\sqrt{2}\)
c) \((x^2-1)(0,6x+1)=0,6x^2+x\)
\(⇔(x^2-1)(0,6x+1)=x.(0,6x+1)\)
\(⇔(x^2-1)(0,6x+1)-x(0,6x+1)=0\)
\(⇔(0,6x+1)(x^2-1-x)=0\)
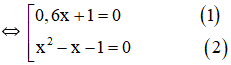
+ Giải (1): 0,6x + 1 = 0 ⇔ \(x=\frac{-5}{3}\)
+ Giải (2):
\(x^2-x-1=0\)
Có \(a=1;b=-1;c=-1\)
\(⇒Δ=(-1)^2-4.1.(-1)=5>0\)
⇒ (2) có hai nghiệm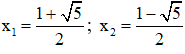 
Vậy phương trình có tập nghiệm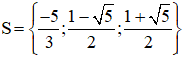 
d) \((x^2+2x-5)^2=(x^2-x+5)^2\)
\(⇔(x^2+2x-5)^2-(x^2-x+5)^2=0\)
\(⇔[(x^2+2x-5)-(x^2-x+5)].[(x^2+2x-5)+(x^2-x+5)]=0\)
\(⇔(3x-10)(2x^2+x-10)=0\)
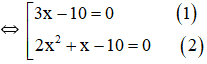
+ Giải (1): 3x – 10 = 0 ⇔ \(x=\frac{10}{3}\)
+ Giải (2):
\(2x^2+x-10=0\)
Có \(a=2;b=1;c=-10\)
\(⇒Δ=12-4.2.(-10)=81>0\)
⇒ (2) có hai nghiệm:
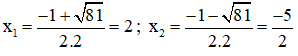
Vậy phương trình có tập nghiệm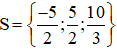 
Bài 40 (trang 57 SGK Toán 9 tập 2): Giải phương trình bằng cách đặt ẩn phụ:
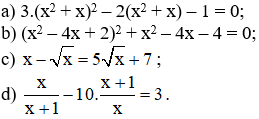
Hướng dẫn:
a) Đặt t = x2 + x, ta có phương trình 3t2 - 2t - 1 = 0. Giải phương trình này, ta tìm được hai giá trị của t. Thay mỗi giá trị của t vừa tìm được vào đẳng thức t = x2 +x, ta được một phương trình của ẩn x. Giải mỗi phương trình này sẽ tìm được giá trị của x.
Lời giải
a) \(3.(x^2+x)^2-2(x^2+x)-1=0(1)\)
Đặt \(t=x^2+x\),
Khi đó (1) trở thành: \(3t^2-2t-1=0(2)\)
Giải (2): Có \(a=3;b=-2;c=-1\)
\(⇒a+b+c=0\)
⇒ (2) có hai nghiệm \(t_1=1;t_2=\frac{c}{a}=\frac{-1}{3}\)
+ Với \(t=1⇒x^2+x=1⇔x^2+x-1=0(*)\)
Có \(a=1;b=1;c=-1⇒Δ=1^2-4.1.(-1)=5>0\)
(*) có hai nghiệm
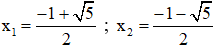
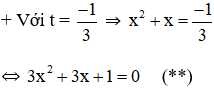
Có \(a=3;b=3;c=1⇒Δ=3^2-4.3.1=-3<0\)
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm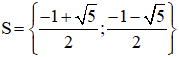 
b) \((x^2-4x+2)^2+x^2-4x-4=0\)
\(⇔(x^2-4x+2)^2+x^2-4x+2-6=0(1)\)
Đặt \(x^2-4x+2=t,\)
Khi đó (1) trở thành:\(t^2+t-6=0(2)\)
Giải (2): Có \(a=1;b=1;c=-6\)
\(⇒Δ=1^2-4.1.(-6)=25>0\)
⇒ (2) có hai nghiệm
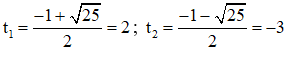
+ Với \(t=2⇒x^2-4x+2=2\)
\(⇔x^2-4x=0\)
\(⇔x(x-4)=0\)
⇔ x = 0 hoặc x = 4.
+ Với \(t=-3⇒x^2-4x+2=-3\)
\(⇔x^2-4x+5=0(*)\)
Có \(a=1;b=-4;c=5⇒Δ’=(-2)^2-1.5=-1<0\)
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
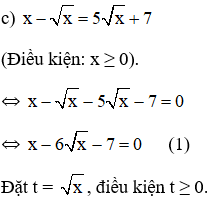
Khi đó (1) trở thành:\(t^2-6t-7=0(2)\)
Giải (2): Có \(a=1;b=-6;c=-7\)
\(⇒a-b+c=0\)
⇒ (2) có nghiệm \(t_1=-1;t_2=\frac{-c}{a}=7.\)
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với \(t=7⇒\sqrt{x}=7⇔x=49\) (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
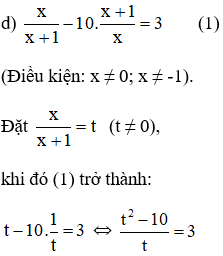
\(⇔t^2-10=3t⇔t^2-3t-10=0(2)\)
Giải (2): Có \(a=1;b=-3;c=-10\)
⇒ Δ = (-3)2 - 4.1.(-10) = 49 > 0
⇒ (2) có hai nghiệm:
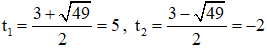
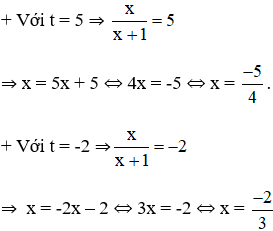
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm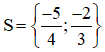 
Bài tiếp theo: Giải Toán 9 bài 8: Giải bài toán bằng cách lập phương trình
....................................
Ngoài Giải bài tập SGK Toán lớp 9 bài 7: Phương trình quy về phương trình bậc hai. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt
