Giải bài tập SGK Toán lớp 9 bài 2: Đồ thị hàm số y = ax2 (a ≠ 0)
Giải bài tập Toán lớp 9 bài 2: Đồ thị hàm số y = ax2 (a ≠ 0)
Nhằm giúp quá trình ôn tập và củng cố kiến thức chuẩn bị cho kì thi học kì mới môn Toán lớp 9 của các bạn học sinh trở nên thuận lợi hơn chúng tôi xin giới thiệu với các bạn bài: Giải bài tập SGK Toán lớp 9 bài 2: Đồ thị hàm số y = ax2 (a ≠ 0). Mời các bạn cùng tham khảo
- Giải bài tập SGK Toán lớp 9 bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
- Giải bài tập SGK Toán lớp 9 bài 5: Giải bài toán bằng cách lập hệ phương trình
- Giải bài tập SGK Toán lớp 9 bài 6: Giải bài toán bằng cách lập hệ phương trình (Tiếp theo)
- Giải bài tập SGK Toán lớp 9: Ôn tập chương 3
Trả lời câu hỏi Toán 9 Tập 2 Bài 2 trang 34: Hãy nhận xét một vài đặc điểm của đồ thị này bằng cách trả lời các câu hỏi sau (h.6):
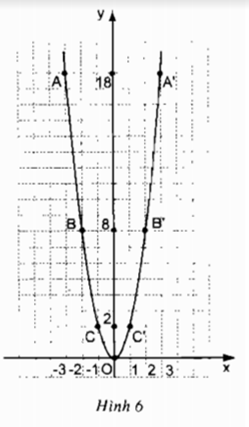
- Đồ thị nằm ở phía trên hay phía dưới trục hoành?
- Vị trí của cặp điểm A, A’ đối với trục Oy? Tương tự đối với các điểm B, B’ và C, C’?
- Điểm nào là điểm thấp nhất của đồ thị?
Lời giải
Đồ thị nằm ở phía trên trục hoành
- Các cặp điểm A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm thấp nhất của đồ thị.
Trả lời câu hỏi Toán 9 Tập 2 Bài 2 trang 34: Nhận xét một vài đặc điểm của đồ thị và rút ra những kết luận, tương tự như đã làm đối với hàm y = 2x2.
Lời giải
- Đồ thị nằm ở phía dưới trục hoành
- Các cặp điểm M và M’; N và N’; P và P’ đối xứng nhau qua trục Oy
- Điểm O (0;0) là điểm cao nhất của đồ thị.
Trả lời câu hỏi Toán 9 Tập 2 Bài 2 trang 35: Cho hàm số y = (-1)/2 x2.
a) Trên đồ thị của hàm số này, xác định điểm D có hoành độ bằng 3. Tìm tung độ của điểm D bằng hai cách: bằng đồ thị; bằng cách tính y với x = 3. So sánh hai kết quả.
b) Trên đồ thị làm số này, xác định điểm có tung độ bằng -5. Có mấy điểm như thế? Không làm tính, hãy ước lượng giá trị hoành độ của mỗi điểm.
Lời giải
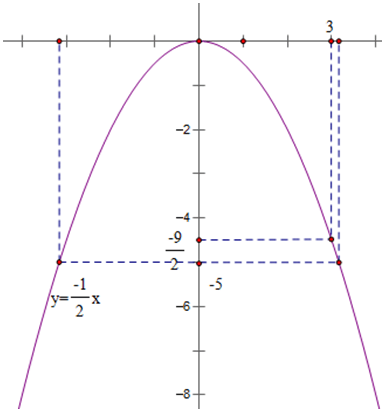
a) Từ đồ thị, ta xác định được tung độ của điểm D là (-9)/2
Với x = 3 ta có: y = (-1)/2 x2 = (-1)/2.32 = (-9)/2
Hai kết quả là như nhau.
b) Có 2 điểm có tung độ bằng -5
Giá trị của hoành độ là ≈ 3,2
Bài 4 (trang 36 SGK Toán 9 tập 2): Cho hai hàm số ![]() \(y=\frac{3}{2}x^2\) và
\(y=\frac{3}{2}x^2\) và ![]() \(y=\frac{-3}{2}x^2\). Điền vào chỗ trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
\(y=\frac{-3}{2}x^2\). Điền vào chỗ trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
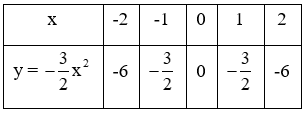
| x | -2 | -1 | 0 | 1 | 2 |
| x | -2 | -1 | 0 | 1 | 2 |
Nhận xét về tính đối xứng của hai đồ thị đối với trục Ox.
Lời giải
+ Điền vào ô trống:
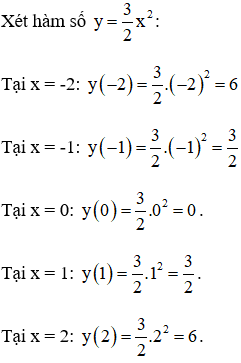
Vậy ta có bảng:
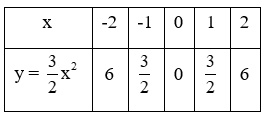
Tương tự như vậy với hàm số ![]() \(y=\frac{-3}{2}x^2\) . Ta có bảng:
\(y=\frac{-3}{2}x^2\) . Ta có bảng:
+ Vẽ đồ thị hàm số:
Trên mặt phẳng lưới lấy các điểm A(-2; 6); ![]() \(B\left(-1;\frac{3}{2}\right)\); O(0; 0);
\(B\left(-1;\frac{3}{2}\right)\); O(0; 0); ![]() \(C\left(1;\frac{3}{2}\right)\); D(2; 6).
\(C\left(1;\frac{3}{2}\right)\); D(2; 6).
Nối các điểm trên theo một đường cong ta được parabol ![]() \(y=\frac{3}{2}x^2\)
\(y=\frac{3}{2}x^2\)
Lấy các điểm A’ (-2; -6); ![]() \(B'\left(-1;\frac{-3}{2}\right)\); O(0; 0);
\(B'\left(-1;\frac{-3}{2}\right)\); O(0; 0); ![]() \(C'\left(1;\frac{-3}{2}\right)\); D’(2; -6).
\(C'\left(1;\frac{-3}{2}\right)\); D’(2; -6).
Nối các điểm trên theo một đường cong ta được parabol ![]() \(y=-\frac{3}{2}x^2\)
\(y=-\frac{3}{2}x^2\)
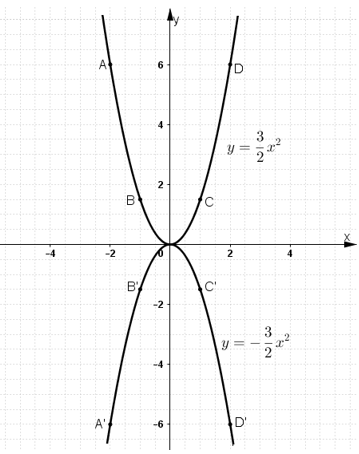
Nhận xét: Đồ thị hàm số ![]() \(y=\frac{3}{2}x^2\)và
\(y=\frac{3}{2}x^2\)và ![]() \(y=\frac{-3}{2}x^2\) đối xứng nhau qua trục Ox.
\(y=\frac{-3}{2}x^2\) đối xứng nhau qua trục Ox.
Bài 5 (trang 37 SGK Toán 9 tập 2): Cho ba hàm số:
![]()
a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.
c) Tìm ba điểm A’; B’; C’ có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A’; B và B’; C và C’.
d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.
Lời giải
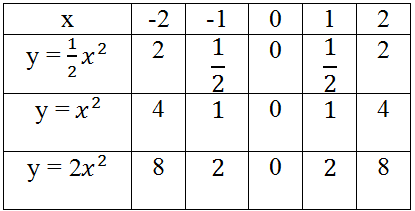
a) Bảng giá trị tương ứng của x và y:
Vẽ đồ thị:
Trên mặt phẳng lưới lấy các điểm (-2; 2); (-1; ½); (0; 0); (1; 1/2); (2; 2), nối chúng thành một đường cong ta được đồ thị hàm số y = ½.x2.
Lấy các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4), nối chúng thành một đường cong ta được đồ thị hàm số y = x2.
Lấy các điểm (-2; 8); (-1; 2); (0; 0); (1; 2); (2; 8), nối chúng thành một đường cong ta được đồ thị hàm số y = 2x2.
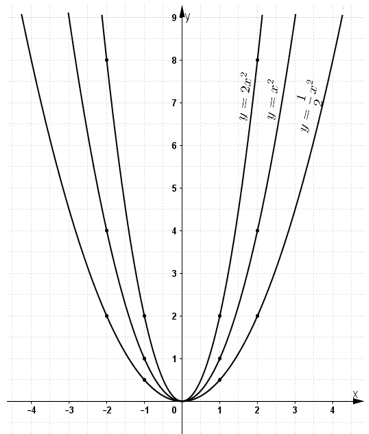
b) Lấy các điểm A, B, C lần lượt nằm trên 3 đồ thị và có hoành độ bằng -1,5.
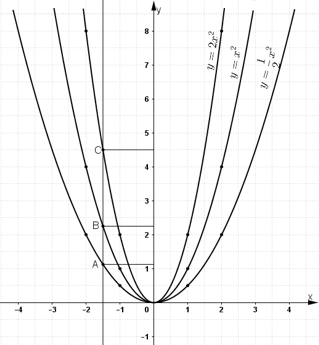
Khi đó tung độ điểm A bằng 9/8; tung độ điểm B bằng 9/4; tung độ điểm C bằng 9/2
c)
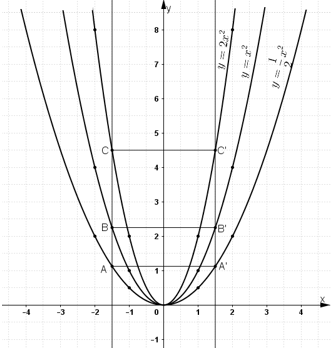
Lấy các điểm A’, B’, C’ lần lượt nằm trên 3 đồ thị và có hoành độ bằng 1,5.
Khi đó 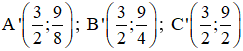
Nhận xét: A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy.
d) Hàm số có giá trị nhỏ nhất ⇔ y nhỏ nhất.
Dựa vào đồ thị nhận thấy cả ba hàm số đạt y nhỏ nhất tại điểm O(0; 0).
Vậy ba hàm số trên đều đạt giá trị nhỏ nhất tại x = 0.
Luyện tập (trang 38-39)
Bài 6 (trang 38 SGK Toán 9 tập 2): Cho hàm số y = f(x) = x2.
a) Vẽ đồ thị của hàm số đó.
b) Tính các giá trị f(-8); f(-1,3); f(-0,75); f(1,5).
c) Dùng đồ thị để ước lượng các giá trị (0,5)2; (-1,5)2; (2,5)2.
d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số √3 ; √7.
Lời giải
a) Ta có bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| y = x2 | 4 | 1 | 0 | 1 | 4 |
Vẽ đồ thị hàm số :
Trên hệ trục tọa độ xác định các điểm (-2 ; 4) ; (-1 ; 1) ; (0 ; 0) ; (1 ; 1) ; (2 ; 4). Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = x2.
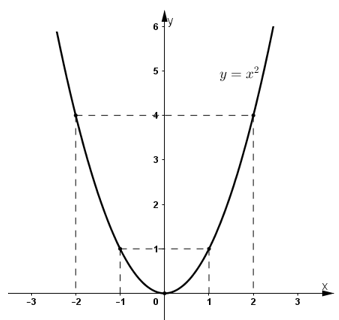
b) f(-8) = (-8)2 = 64
f(-1,3) = (-1,3)2 = 1,69
f(-0,75) = (-0,75)2 = 0,5625
f(1,5) = (1,5)2 = 2,25.
c)
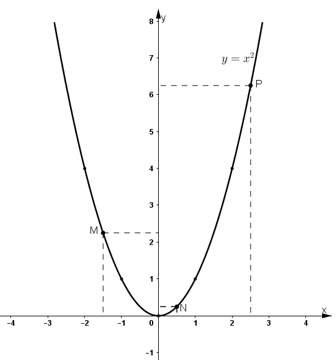
Trên đồ thị hàm số, lấy các điểm M, N, P có hoành độ lần lượt bằng -1,5; 0,5 và 2,5.
Dựa vào đồ thị nhận thấy các điểm M, N, P có tọa độ là: M(-1,5 ; 2,25); N(0,5 ; 0,25); P(2,5 ; 6,25).
Vậy (0,5)2 = 2,25; (-1,5)2 = 2,25; (2,5)2 = 6,25.
d)
Ta có: ![]() \(\left(\sqrt{3}\right)^2=3\);
\(\left(\sqrt{3}\right)^2=3\); ![]() \(\left(\sqrt{7}\right)^2=7\)
\(\left(\sqrt{7}\right)^2=7\)
⇒ Các điểm ![]() \(\left(\sqrt{3};3\right)\) và
\(\left(\sqrt{3};3\right)\) và ![]() \(\left(\sqrt{7};7\right)\) thuộc đồ thị hàm số y = x2.
\(\left(\sqrt{7};7\right)\) thuộc đồ thị hàm số y = x2.
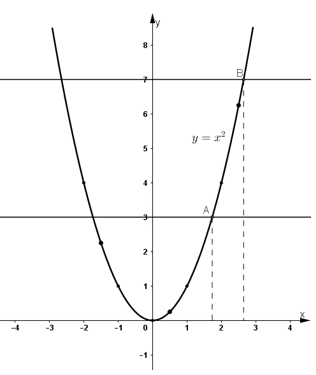
Để xác định các điểm ![]() \(\sqrt{3}\) ;
\(\sqrt{3}\) ; ![]() \(\sqrt{7}\) trên trục hoành, ta lấy trên đồ thị hàm số các điểm A, B có tung độ lần lượt là 3 và 7.
\(\sqrt{7}\) trên trục hoành, ta lấy trên đồ thị hàm số các điểm A, B có tung độ lần lượt là 3 và 7.
Chiếu vuông góc các điểm A, B trên trục hoành ta được các điểm ![]() \(\sqrt{3}\);
\(\sqrt{3}\); ![]() \(\sqrt{7}\) trên đồ thị hàm số.
\(\sqrt{7}\) trên đồ thị hàm số.
a) Tìm hệ số a.
b) Điểm A(4; 4) có thuộc đồ thị không?
c) Hãy tìm thêm hai điểm nữa(không kể điểm O) để vẽ đồ thị.
Lời giải
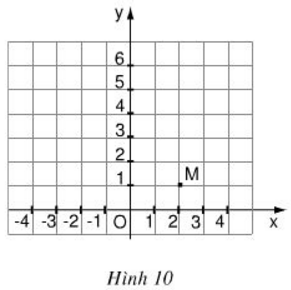
a) Dựa trên hình 10 ta thấy điểm M có tọa độ (2; 1).
M thuộc đồ thị hàm số y = ax2
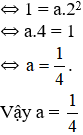
b) Với x = 4 ta có ![]()
Vậy điểm A(4 ; 4) thuộc đồ thị hàm số ![]() \(y=\frac{1}{4}x^2\)
\(y=\frac{1}{4}x^2\)
c) Chọn x = -2 ⇒ ![]()
Vậy (-2; 1) thuộc đồ thị hàm số.
Chọn x = -4 ⇒ ![]()
Vậy (-4; 4) thuộc đồ thị hàm số.
* Vẽ đồ thị:
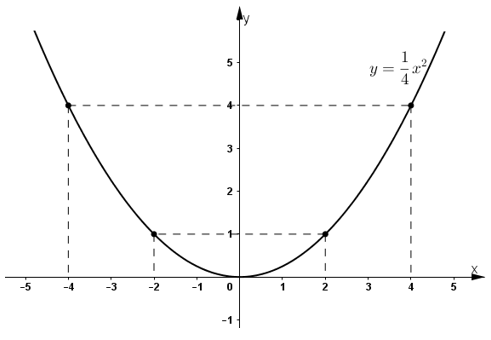
Bài 8 (trang 38 SGK Toán 9 tập 2): Biết rằng đường cong trong hình 11 là một parapol y = ax2.
a) Tìm hệ số a.
b) Tìm tung đệ của điểm thuộc parapol có hoành độ x = -3.
c) Tìm các điểm thuộc parapol có tung độ y = 8.
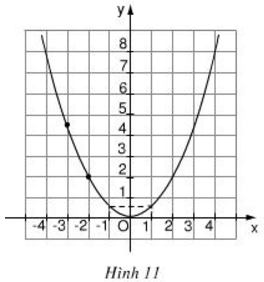
Lời giải
a) Ta có đồ thị hàm số y = ax2 đi qua điểm (-2 ; 2)
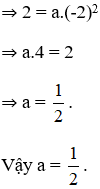
b) Tại x = -3 ta có: ![]()
Vậy điểm có hoành độ x = -3 thì tung độ bằng 4,5.
c) Ta có: y = 8 ⇔ ![]() \(\frac{1}{2}x^2=8\) ⇔ x2 = 16 ⇔ x = 4 hoặc x = -4.
\(\frac{1}{2}x^2=8\) ⇔ x2 = 16 ⇔ x = 4 hoặc x = -4.
Vậy các điểm thuộc parabol có tung độ bằng 8 là (4; 8) và (-4; 8).
Bài 9 (trang 39 SGK Toán 9 tập 2): Cho hai hàm số ![]() \(y=\frac{1}{3}x^2\) và y = -x + 6.
\(y=\frac{1}{3}x^2\) và y = -x + 6.
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị đó.
Lời giải
a)
- Vẽ đường thẳng y = -x + 6
Cho x = 0 ⇒ y = 6 được điểm (0, 6)
Cho x = 6 ⇒ y = 0 được điểm (6, 0)
⇒ Đường thẳng y = -x + 6 đi qua các điểm (6; 0) và (0; 6).
- Lập bảng giá trị và vẽ đồ thị hàm số ![]() \(y=\frac{1}{3}x^2\)
\(y=\frac{1}{3}x^2\)
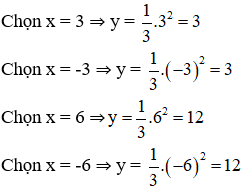
⇒ Parabol đi qua các điểm (3; 3); (-3; 3); (-6; 12); (6; 12); (0; 0).
b) Dựa vào đồ thị ta nhận thấy giao điểm của hai đồ thị là A(-6; 12) và (3; 3).
Bài 10 (trang 39 SGK Toán 9 tập 2): Cho hàm số y = -0,75x2. Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?
Lời giải
- Lập bảng giá trị:
| x | -4 | -2 | 0 | 2 | 4 |
| y = -0,75x2 | -12 | -3 | 0 | -3 | -12 |
- Vẽ đồ thị:
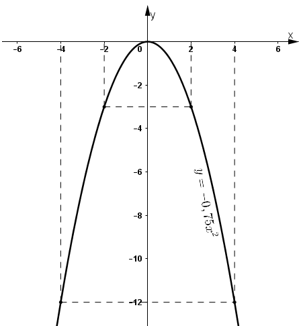
- Quan sát đồ thị hàm số y = -0,75x2:
Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.
Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4
Giá trị lớn nhất của y = 0 đạt được khi x = 0.
....................................
Ngoài Giải bài tập SGK Toán lớp 9 bài 2: Đồ thị hàm số y = ax2 (a ≠ 0). Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt








