Giải Toán 9 bài 6: Hệ thức Vi-ét và ứng dụng
Giải Toán 9 bài 6 tập 2: Hệ thức Vi-ét và ứng dụng
Giải bài tập Toán 9 bài 6: Hệ thức Vi-ét và ứng dụng tổng hợp câu hỏi và đáp án cho các câu hỏi trong SGK Toán 9, giúp các em biết cách trả lời câu hỏi trong bài, từ đó học tốt môn Toán hơn. Tài liệu được biên soạn chi tiết dễ hiểu giúp các em nắm chắc kiến thức được học trong bài. Mời các bạn tham khảo chi tiết sau đây.
Trả lời câu hỏi Toán 9 Tập 2 Bài 6 trang 50: Hãy tính  \(x_1+x_2,x_1x_2\).
\(x_1+x_2,x_1x_2\).

Lời giải

Trả lời câu hỏi Toán 9 Tập 2 Bài 6 trang 51: Cho phương trình \(2x^2-5x+3=0\).
\(2x^2-5x+3=0\).
a) Xác định các hệ số a, b, c rồi tính ![]() \(a+b+c.\)
\(a+b+c.\)
b) Chứng tỏ rằng x1 = 1 là một nghiệm của phương trình.
c) Dùng định lý Vi-ét để tìm x2.
Lời giải
a) ![]() \(a=2;b=-5;c=3\)
\(a=2;b=-5;c=3\)
![]() \(⇒a+b+c=2-5+3=0\)
\(⇒a+b+c=2-5+3=0\)
b) Thay x = 1 vào phương trình ta được:
![]() \(2.1^2-5.1+3=0\)
\(2.1^2-5.1+3=0\)
Vậy x = 1 là một nghiệm của phương trình
c) Theo định lí Vi-et ta có:
![]() \(x_1.x_2=\frac{c}{a}=\frac{3}{2}⇒x_2=\frac{3}{2}\)
\(x_1.x_2=\frac{c}{a}=\frac{3}{2}⇒x_2=\frac{3}{2}\)
Trả lời câu hỏi Toán 9 Tập 2 Bài 6 trang 51: Cho phương trình  \(3x^2+7x+4=0\).
\(3x^2+7x+4=0\).
a) Xác định các hệ số a, b, c rồi tính a - b + c.
b) Chứng tỏ rằng x1 = -1 là một nghiệm của phương trình.
c) Tìm nghiệm x2.
Lời giải
a) ![]() \(a=3;b=7;c=4\)
\(a=3;b=7;c=4\)
![]() \(⇒a+b+c=3-7+4=0\)
\(⇒a+b+c=3-7+4=0\)
b) Thay ![]() \(x=-1\) vào phương trình ta được:
\(x=-1\) vào phương trình ta được:
![]() \(3.(-1)^2+7.(-1)+4=0\)
\(3.(-1)^2+7.(-1)+4=0\)
Vậy x = - 1 là một nghiệm của phương trình
c) Theo định lí Vi-et ta có:
![]() \(x_1.x_2=\frac{c}{a}=\frac{4}{3}⇒x_2=\frac{4}{3}:(-1)=\frac{-4}{3}\)
\(x_1.x_2=\frac{c}{a}=\frac{4}{3}⇒x_2=\frac{4}{3}:(-1)=\frac{-4}{3}\)
Trả lời câu hỏi Toán 9 Tập 2 Bài 6 trang 51: Cho phương trình  \(2x^2-5x+3=0\).
\(2x^2-5x+3=0\).
a) Xác định các hệ số a, b, c rồi tính a + b + c.
b) Chứng tỏ rằng x1 = 1 là một nghiệm của phương trình.
c) Dùng định lý Vi-ét để tìm x2.
Lời giải
a)![]() \(a=2;b=-5;c=3\)
\(a=2;b=-5;c=3\)
![]() \(⇒a+b+c=2-5+3=0\)
\(⇒a+b+c=2-5+3=0\)
b) Thay x = 1 vào phương trình ta được:
![]() \(2.1^2-5.1+3=0\)
\(2.1^2-5.1+3=0\)
Vậy x = 1 là một nghiệm của phương trình
c) Theo định lí Vi-et ta có:
![]() \(x_1.x_2=\frac{c}{a}=\frac{3}{2}⇒x_2=\frac{3}{2}\)
\(x_1.x_2=\frac{c}{a}=\frac{3}{2}⇒x_2=\frac{3}{2}\)
Trả lời câu hỏi Toán 9 Tập 2 Bài 6 trang 51: Cho phương trình  \(3x^2+7x+4=0\).
\(3x^2+7x+4=0\).
a) Xác định các hệ số a, b, c rồi tính ![]() \(a-b+c.\)
\(a-b+c.\)
b) Chứng tỏ rằng ![]() \(x_1=-1\) là một nghiệm của phương trình.
\(x_1=-1\) là một nghiệm của phương trình.
c) Tìm nghiệm x2.
Lời giải
a) ![]() \(a=3;b=7;c=4\)
\(a=3;b=7;c=4\)
![]() \(⇒a+b+c=3-7+4=0\)
\(⇒a+b+c=3-7+4=0\)
b) Thay x = -1 vào phương trình ta được:
![]() \(3.(-1)^2+7.(-1)+4=0\)
\(3.(-1)^2+7.(-1)+4=0\)
Vậy x = - 1 là một nghiệm của phương trình
c) Theo định lí Vi-et ta có:
![]() \(x_1.x_2=\frac{c}{a}=\frac{4}{3}⇒x_2=\frac{4}{3}:(-1)=\frac{-4}{3}\)
\(x_1.x_2=\frac{c}{a}=\frac{4}{3}⇒x_2=\frac{4}{3}:(-1)=\frac{-4}{3}\)
Trả lời câu hỏi Toán 9 Tập 2 Bài 6 trang 52: Tính nhẩm nghiệm của các phương trình:
a) ![]() \(-5x^2+3x+2=0\);
\(-5x^2+3x+2=0\);
b) ![]() \(2004x^2+2005x+1=0\).
\(2004x^2+2005x+1=0\).
Lời giải
a) ![]() \(-5x^2+3x+2=0\);
\(-5x^2+3x+2=0\);
Nhận thấy phương trình có ![]() \(a+b+c=0\) nên phương trình có 2 nghiệm
\(a+b+c=0\) nên phương trình có 2 nghiệm
![]() \(x_1=1;x_2=\frac{c}{a}=\frac{-2}{5}\)
\(x_1=1;x_2=\frac{c}{a}=\frac{-2}{5}\)
b) ![]() \(2004x^2+2005x+1=0\)
\(2004x^2+2005x+1=0\)
Nhận thấy phương trình có ![]() \(a-b+c=0\) nên phương trình có 2 nghiệm
\(a-b+c=0\) nên phương trình có 2 nghiệm
![]() \(x_1=-1;x_2=\frac{-c}{a}=\frac{-1}{2004}\)
\(x_1=-1;x_2=\frac{-c}{a}=\frac{-1}{2004}\)
Trả lời câu hỏi Toán 9 Tập 2 Bài 6 trang 52: Tìm hai số biết tổng của chúng bằng 1, tích của chúng bằng 5.
Lời giải
Hai số cần tìm là nghiệm của phương trình ![]() \(x^2-x+5=0\)
\(x^2-x+5=0\)
![]() \(Δ=b^2-4ac=(-1)^2-4.1.5=-19<0\)
\(Δ=b^2-4ac=(-1)^2-4.1.5=-19<0\)
⇒ phương trình vô nghiêm
Vậy không tồn tại 2 số có tổng bằng 1 và tích bằng 5
Bài 25 (trang 52 SGK Toán 9 tập 2): Đối với mỗi phương trình sau, kí hiệu x1 và x2 là hai nghiệm (nếu có). Không giải phương trình, hãy điền vào những chỗ trống (...):
a) ![]() \(2x^2-17x+1=0\);
\(2x^2-17x+1=0\);
![]() \(Δ=\dots;x_1+x_2=\dots;x_1.x_2=\dots;\)
\(Δ=\dots;x_1+x_2=\dots;x_1.x_2=\dots;\)
b) ![]() \(5x^2-x-35=0\);
\(5x^2-x-35=0\);
![]() \(Δ=\dots;x_1+x_2=\dots;x_1.x_2=\dots;\)
\(Δ=\dots;x_1+x_2=\dots;x_1.x_2=\dots;\)
c) ![]() \(8x^2-x+1=0\);
\(8x^2-x+1=0\);
![]() \(Δ=\dots;x_1+x_2=\dots;x_1.x_2=\dots;\)
\(Δ=\dots;x_1+x_2=\dots;x_1.x_2=\dots;\)
d)![]() \(25x^2+10x+1=0\);
\(25x^2+10x+1=0\);
![]() \(25x^2+10x+1=0\)
\(25x^2+10x+1=0\)
Lời giải
a) ![]() \(2x^2-17x+1=0\)
\(2x^2-17x+1=0\)
Có ![]() \(a=2;b=-17;c=1\)
\(a=2;b=-17;c=1\)
![]() \(Δ=b^2-4ac=(-17)^2-4.2.1=281>0.\)
\(Δ=b^2-4ac=(-17)^2-4.2.1=281>0.\)
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
![]() \(x_1+x_2=\frac{-b}{a}=\frac{17}{2}\)
\(x_1+x_2=\frac{-b}{a}=\frac{17}{2}\)
![]() \(x_1.x_2=\frac{c}{a}=\frac{1}{2}.\)
\(x_1.x_2=\frac{c}{a}=\frac{1}{2}.\)
b) ![]() \(5x^2-x-35=0\)
\(5x^2-x-35=0\)
Có ![]() \(a=5;b=-1;c=-35\);
\(a=5;b=-1;c=-35\);
![]() \(Δ=b^2-4ac=(-1)^2-4.5.(-35)=701>0\)
\(Δ=b^2-4ac=(-1)^2-4.5.(-35)=701>0\)
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
![]() \(x_1+x_2=\frac{-b}{a}=\frac{1}{5}\)
\(x_1+x_2=\frac{-b}{a}=\frac{1}{5}\)
![]() \(x_1.x_2=\frac{c}{a}=\frac{-35}{5}=-7.\)
\(x_1.x_2=\frac{c}{a}=\frac{-35}{5}=-7.\)
c) ![]() \(8x^2-x+1=0\)
\(8x^2-x+1=0\)
Có ![]() \(a=8;b=-1;c=1\)
\(a=8;b=-1;c=1\)
![]() \(Δ=b^2-4ac=(-1)^2-4.8.1=-31<0\)
\(Δ=b^2-4ac=(-1)^2-4.8.1=-31<0\)
Phương trình vô nghiệm nên không tồn tại x1; x2.
d) ![]() \(25x^2+10x+1=0^{ }\)
\(25x^2+10x+1=0^{ }\)
Có ![]() \(a=25;b=10;c=1\)
\(a=25;b=10;c=1\)
![]() \(Δ=b^2-4ac=10^2-4.25.1=0\)
\(Δ=b^2-4ac=10^2-4.25.1=0\)
Khi đó theo hệ thức Vi-et có:
![]() \(x_1+x_2=\frac{-b}{a}=\frac{-10}{25}=\frac{-2}{5}\)
\(x_1+x_2=\frac{-b}{a}=\frac{-10}{25}=\frac{-2}{5}\)
![]() \(x_1.x_2=\frac{c}{a}=\frac{1}{25}.\)
\(x_1.x_2=\frac{c}{a}=\frac{1}{25}.\)
Bài 26 (trang 53 SGK Toán 9 tập 2): Dùng điều kiện  \(a+b+c=0\) hoặc
\(a+b+c=0\) hoặc  \(a-b+c=0\) để tính nhẩm nghiệm của mỗi phương trình sau:
\(a-b+c=0\) để tính nhẩm nghiệm của mỗi phương trình sau:
a) ![]() \(35x^2-37x+2=0\);
\(35x^2-37x+2=0\);
b) ![]() \(7x^2+500x-507=0\);
\(7x^2+500x-507=0\);
c) ![]() \(x^2-49x-50=0\);
\(x^2-49x-50=0\);
d) ![]() \(4321x^2+21x-4300=0\).
\(4321x^2+21x-4300=0\).
Lời giải
a) Phương trình ![]() \(35x^2-37x+2=0\)
\(35x^2-37x+2=0\)
Có ![]() \(a=35;b=-37;c=2⇒a+b+c=0\)
\(a=35;b=-37;c=2⇒a+b+c=0\)
⇒ Phương trình có nghiệm ![]() \(x_1=1;x_2=\frac{c}{a}=\frac{2}{35}\).
\(x_1=1;x_2=\frac{c}{a}=\frac{2}{35}\).
b) Phương trình ![]() \(7x^2+500x-507=0\)
\(7x^2+500x-507=0\)
Có ![]() \(a=7;b=500;c=-507⇒a+b+c=7+500-507=0\)
\(a=7;b=500;c=-507⇒a+b+c=7+500-507=0\)
⇒ Phương trình có nghiệm ![]() \(x_1=1;x_2=\frac{c}{a}=\frac{-507}{7}\).
\(x_1=1;x_2=\frac{c}{a}=\frac{-507}{7}\).
c) Phương trình ![]() \(x^2-49x-50=0\)
\(x^2-49x-50=0\)
Có ![]() \(a=1;b=-49;c=-50⇒a-b+c=1-(-49)-50=0\)
\(a=1;b=-49;c=-50⇒a-b+c=1-(-49)-50=0\)
⇒ Phương trình có nghiệm ![]() \(x_1=-1;x_2=\frac{-c}{a}=50\).
\(x_1=-1;x_2=\frac{-c}{a}=50\).
d) Phương trình ![]() \(4321x^2+21x-4300=0\)
\(4321x^2+21x-4300=0\)
Có ![]() \(a=4321;b=21;c=-4300⇒a-b+c=4321-21-4300=0\)
\(a=4321;b=21;c=-4300⇒a-b+c=4321-21-4300=0\)
⇒ Phương trình có nghiệm ![]() \(x_1=-1;x_2=\frac{-c}{a}=\frac{4300}{4321}\).
\(x_1=-1;x_2=\frac{-c}{a}=\frac{4300}{4321}\).
Bài 27 (trang 53 SGK Toán 9 tập 2): Dùng hệ thức Vi-et để tính nhẩm các nghiệm của phương trình.
a) ![]() \(x^2-7x+12=0\);
\(x^2-7x+12=0\);
b) ![]() \(x^2+7x+12=0\).
\(x^2+7x+12=0\).
Lời giải
a) ![]() \(x^2-7x+12=0\)
\(x^2-7x+12=0\)
Có ![]() \(a=1;b=-7;c=12\)
\(a=1;b=-7;c=12\)
![]() \(⇒Δ=b^2-4ac=(-7)^2-4.1.12=1>0\)
\(⇒Δ=b^2-4ac=(-7)^2-4.1.12=1>0\)
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:

Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.
b) ![]() \(x^2+7x+12=0\)
\(x^2+7x+12=0\)
Có ![]() \(a=1;b=7;c=12\)
\(a=1;b=7;c=12\)
![]() \(⇒Δ=b^2-4ac=7^2-4.1.12=1>0\)
\(⇒Δ=b^2-4ac=7^2-4.1.12=1>0\)
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:

Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.
Bài 28 (trang 53 SGK Toán 9 tập 2): Tìm hai số u và v trong mỗi trường hợp sau:
a) ![]() \(u+v=32,uv=231\)
\(u+v=32,uv=231\)
b) ![]() \(u+v=-8,uv=-105\)
\(u+v=-8,uv=-105\)
c) ![]() \(u+v=2,uv=9\)
\(u+v=2,uv=9\)
Lời giải
a) ![]() \(S=32;P=231⇒S^2-4P=32^{^{^2}}-4.231=100>0\)
\(S=32;P=231⇒S^2-4P=32^{^{^2}}-4.231=100>0\)
⇒ Tồn tại u và v là hai nghiệm của phương trình: ![]() \(x^2-32x+231=0\).
\(x^2-32x+231=0\).
Ta có: ![]() \(Δ=(-32)^2-4.231=100>0\)
\(Δ=(-32)^2-4.231=100>0\)
⇒ PT có hai nghiệm:

Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.
b) ![]() \(S=-8;P=-105⇒S^2-4P=(-8)^2-4.(-105)=484>0\)
\(S=-8;P=-105⇒S^2-4P=(-8)^2-4.(-105)=484>0\)
⇒ u và v là hai nghiệm của phương trình: ![]() \(x^2+8x-105=0\)
\(x^2+8x-105=0\)
Ta có: ![]() \(Δ’=4^2-1.(-105)=121>0\)
\(Δ’=4^2-1.(-105)=121>0\)
Phương trình có hai nghiệm:

Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.
c) ![]() \(S=2;P=9⇒S^2-4P=2^2-4.9=-34<0\)
\(S=2;P=9⇒S^2-4P=2^2-4.9=-34<0\)
⇒ Không tồn tại u và v thỏa mãn.
Luyện tập (trang 54)
Bài 29 (trang 54 SGK Toán 9 tập 2): Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:
a) ![]() \(4x^2+2x-5=0\);
\(4x^2+2x-5=0\);
b) ![]() \(9x^2-12x+4=0\);
\(9x^2-12x+4=0\);
c)![]() \(5x^2+x+2=0\);
\(5x^2+x+2=0\);
d) ![]() \(159x^2-2x-1=0\).
\(159x^2-2x-1=0\).
Lời giải
a) Phương trình ![]() \(4x^2+2x-5=0\)
\(4x^2+2x-5=0\)
Có ![]() \(a=4;b=2;c=-5,a.c<0\)
\(a=4;b=2;c=-5,a.c<0\)
⇒ Phương trình có hai nghiệm x1; x2
Theo hệ thức Vi-et ta có: 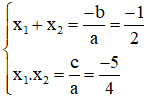
b) Phương trình ![]() \(9x^2-12x+4=0\)
\(9x^2-12x+4=0\)
Có ![]() \(a=9;b=-12;c=4⇒Δ’=(-6)^2-4.9=0\)
\(a=9;b=-12;c=4⇒Δ’=(-6)^2-4.9=0\)
⇒ Phương trình có nghiệm kép x1 = x2.
Theo hệ thức Vi-et ta có: 
c) Phương trình ![]() \(5x^2+x+2=0\)
\(5x^2+x+2=0\)
Có ![]() \(a=5;b=1;c=2⇒Δ=1^2-4.2.5=-39<0\)
\(a=5;b=1;c=2⇒Δ=1^2-4.2.5=-39<0\)
⇒ Phương trình vô nghiệm.
d) Phương trình ![]() \(159x^2-2x-1=0\)
\(159x^2-2x-1=0\)
Có ![]() \(a=159;b=-2;c=-1;a.c<0\)
\(a=159;b=-2;c=-1;a.c<0\)
⇒ Phương trình có hai nghiệm phân biệt x1; x2.
Theo hệ thức Vi-et ta có: 
Bài 30 (trang 54 SGK Toán 9 tập 2): Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích các nghiệm theo m.
a) ![]() \(x^2-2x+m=0\);
\(x^2-2x+m=0\);
b) ![]() \(x^2+2(m-1)x+m^2=0\).
\(x^2+2(m-1)x+m^2=0\).
Lời giải
a) Phương trình ![]() \(x^2-2x+m=0\)
\(x^2-2x+m=0\)
Có ![]() \(a=1;b=-2;c=m\)
\(a=1;b=-2;c=m\)
![]() \(⇒Δ’=(-1)^2-1.m=1-m\)
\(⇒Δ’=(-1)^2-1.m=1-m\)
Phương trình có nghiệm ![]() \(⇔Δ’\ge0⇔1-m\ge0⇔m\le1.\)
\(⇔Δ’\ge0⇔1-m\ge0⇔m\le1.\)
Khi đó, theo định lý Vi-et: 
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
b) Phương trình ![]() \(x^2+2(m-1)x+m^2=0\)
\(x^2+2(m-1)x+m^2=0\)
Có ![]() \(a=1;b=2(m-1);c=m^2\)
\(a=1;b=2(m-1);c=m^2\)
![]() \(⇒Δ’=b'^2-ac=(m-1)^2-m^2=2m-1\).
\(⇒Δ’=b'^2-ac=(m-1)^2-m^2=2m-1\).
Phương trình có nghiệm ![]() \(⇔Δ’\ge0⇔2m-1\ge0⇔m\ge\frac{1}{2}\).
\(⇔Δ’\ge0⇔2m-1\ge0⇔m\ge\frac{1}{2}\).
Khi đó, theo định lý Vi-et: 
Vậy với m ≥ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m2.
Bài 31 (trang 54 SGK Toán 9 tập 2): Tính nhẩm nghiệm của các phương trình:

Lời giải
a) ![]() \(1,5x^2-1,6x+0,1=0\)
\(1,5x^2-1,6x+0,1=0\)
Có ![]() \(a=1,5;b=-1,6;c=0,1\)
\(a=1,5;b=-1,6;c=0,1\)
![]() \(⇒a+b+c=1,5-1,6+0,1=0\)
\(⇒a+b+c=1,5-1,6+0,1=0\)
⇒ Phương trình có hai nghiệm ![]() \(x_1=1;x_q=\frac{c}{a}=\frac{1}{15}\).
\(x_1=1;x_q=\frac{c}{a}=\frac{1}{15}\).

d) ![]() \((m-1)x^2-(2m+3)x+m+4=0\)
\((m-1)x^2-(2m+3)x+m+4=0\)
Có ![]() \(a=m-1;b=-(2m+3);c=m+4\)
\(a=m-1;b=-(2m+3);c=m+4\)
![]() \(⇒a+b+c=(m-1)-(2m+3)+m+4=0\)
\(⇒a+b+c=(m-1)-(2m+3)+m+4=0\)
⇒ Phương trình có hai nghiệm ![]()
Bài 32 (trang 54 SGK Toán 9 tập 2): Tìm hai số u và v trong mỗi trường hợp sau:
a) ![]() \(u+v=42,uv=441\)
\(u+v=42,uv=441\)
b) ![]() \(u+v=-42,uv=-400\)
\(u+v=-42,uv=-400\)
c) ![]() \(u-v=5,uv=24\)
\(u-v=5,uv=24\)
Lời giải
a) ![]() \(S=42;P=441⇒S^2-4P=42^2-4.441=0\)
\(S=42;P=441⇒S^2-4P=42^2-4.441=0\)
⇒ u và v là hai nghiệm của phương trình: ![]() \(x^2-42x+441=0\)
\(x^2-42x+441=0\)
Có: ![]() \(Δ’=(-21)^2-441=0\)
\(Δ’=(-21)^2-441=0\)
⇒ Phương trình có nghiệm kép ![]() \(x_1=x_2=\frac{-b'}{a}=21\).
\(x_1=x_2=\frac{-b'}{a}=21\).
Vậy ![]() \(u=v=21\).
\(u=v=21\).
b) ![]() \(S=-42;P=-400⇒S^2-4P=(-42)^2-4.(-400)=3364>0\)
\(S=-42;P=-400⇒S^2-4P=(-42)^2-4.(-400)=3364>0\)
⇒ u và v là hai nghiệm của phương trình: ![]() \(x^2+42x-400=0\)
\(x^2+42x-400=0\)
Có ![]() \(Δ’=21^2-1.(-400)=841\)
\(Δ’=21^2-1.(-400)=841\)
⇒ Phương trình có hai nghiệm phân biệt:

Vậy u = 8; v = -50 hoặc u = -50; v = 8.
c) ![]() \(u-v=5⇒u+(-v)=5\)
\(u-v=5⇒u+(-v)=5\)
![]() \(u.v=24⇒u.(-v)=-uv=-24\).
\(u.v=24⇒u.(-v)=-uv=-24\).
![]() \(S=5;P=-24⇒S^2-4P=5^2-4.(-24)=121>0\)
\(S=5;P=-24⇒S^2-4P=5^2-4.(-24)=121>0\)
⇒ u và –v là hai nghiệm của phương trình: ![]() \(x^2-5x-24=0\)
\(x^2-5x-24=0\)
Có ![]() \(Δ=(-5)^2-4.1.(-24)=121\)
\(Δ=(-5)^2-4.1.(-24)=121\)
⇒ Phương trình có hai nghiệm phân biệt
![]()
⇒ u = 8; -v = -3 hoặc u = -3; -v = 8
⇒ u = 8; v = 3 hoặc u = -3; v = -8.
Bài 33 (trang 54 SGK Toán 9 tập 2): Chứng tỏ rằng nếu phương trình  \(ax^2+bx+c=0\) có nghiệm là có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
\(ax^2+bx+c=0\) có nghiệm là có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
Áp dụng: phân tích đa thức thành nhân tử.
a) ![]() \(2x^2-5x+3;b)3x^2+8x+2\)
\(2x^2-5x+3;b)3x^2+8x+2\)
Lời giải
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 
Khi đó: ![]() \(a.(x-x_1).(x-x_2)\)
\(a.(x-x_1).(x-x_2)\)
![]() \(=a.(x_2-x_1.x-x_2.x+x_1.x_2)\)
\(=a.(x_2-x_1.x-x_2.x+x_1.x_2)\)
![]() \(=a.x_2-a.x.(x_1+x_2)+a.x_1.x_2\)
\(=a.x_2-a.x.(x_1+x_2)+a.x_1.x_2\)
=![]()
![]() \(=a.x^2+bx+c(đpcm).\)
\(=a.x^2+bx+c(đpcm).\)
* Áp dụng:
a) ![]() \(2x^2-5x+3=0\)
\(2x^2-5x+3=0\)
Có ![]() \(a=2;b=-5;c=3\)
\(a=2;b=-5;c=3\)
![]() \(⇒a+b+c=2-5+3=0\)
\(⇒a+b+c=2-5+3=0\)
⇒ Phương trình có hai nghiệm ![]()
Vậy: ![]() \(2x^2-5x+3=\)
\(2x^2-5x+3=\) 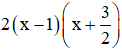
b) ![]() \(3x^2+8x+2=0\)
\(3x^2+8x+2=0\)
Có ![]() \(a=3;b=8;c=2\)
\(a=3;b=8;c=2\)
![]() \(⇒Δ’=42-2.3=10>0\)
\(⇒Δ’=42-2.3=10>0\)
⇒ Phương trình có hai nghiệm phân biệt:

Bài tiếp theo: Giải Toán 9 bài 7: Phương trình quy về phương trình bậc hai
....................................
Ngoài Giải bài tập SGK Toán lớp 9 bài 6: Hệ thức Vi-ét và ứng dụng, các bạn học sinh còn có thể tham khảo các đề thi học học kì 2 lớp 9 các môn Toán 9, Văn 9, Anh 9, Hóa 9, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt.








