Giải bài tập SGK Toán lớp 9 bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Giải bài tập SGK Toán 9 bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Giải bài tập SGK Toán lớp 9 bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt được VnDoc.com sưu tầm và tổng hợp. Lời giải Toán lớp 9 này sẽ giúp các bạn học sinh hệ thống lại những kiến thức đã học trong bài, định hướng phương pháp giải các bài tập cụ thể. Ngoài ra việc tham khảo tài liệu còn giúp các bạn học sinh rèn luyện và nâng cao kỹ năng giải bài tập.
- Giải bài tập SGK Toán lớp 9 bài 9: Độ dài đường tròn, cung tròn
- Giải bài tập SGK Toán lớp 9 bài 9: Độ dài đường tròn, cung tròn
- Giải bài tập SGK Toán lớp 9 bài 10: Diện tích hình tròn, hình quạt tròn
- Giải bài tập SGK Toán lớp 9 bài 1: Hình Trụ - Diện tích xung quanh và thể tích của hình trụ
Trả lời câu hỏi Toán 9 Tập 2 Bài 2 trang 114: Chiếc nón (h.88) có dạng mặt xung quanh là một hình nón. Quan sát hình và cho biết, đâu là đường tròn đáy, đâu là mặt xung quanh, đâu là đường sinh của nón.
Lời giải
Đường tròn đáy là phần vành rộng nhất của nón
Mặt xung quanh là phần bên ngoài của nón, tính từ đỉnh nón đến đường tròn đáy
Đường sinh là đường thẳng bất kì, nối từ đỉnh đến đường tròn đáy
Bài 15 (trang 117 SGK Toán 9 tập 2): Một hình nón được đặt vào bên trong một hình lập phương như hình vẽ (cạnh của hình lập phương bằng 1) (h.93). Hãy tính:
a) Bán kính đáy của hình nón.
b) Độ dài đường sinh.
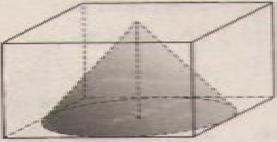
Hình 93
Lời giải
a) Ta có đường tròn đáy của hình nón nội tiếp trong hình vuông của một mặt của hình lập phương. Do đo bán kính của hình tròn đáy của hình nón bằng một nửa của cạnh hình lập phương và bằng 0,5.
b) Đỉnh của hình nón tiếp xúc với một mặt của hình lập phương nên đường cao của hình nón bằng với cạnh của hình lập phương và bằng 1.
Theo định lí Pitago, độ dài đường sinh của hình nón là:
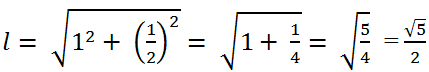
Bài 16 (trang 117 SGK Toán 9 tập 2): Cắt mặt cắt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành một hình quạt. Biết bán kính hình quạt tròn bằng độ dài đường sinh và độ dài cung bằng chu vi đáy.
Quan sát hình 94 và tính số đo cung của hình quạt tròn.
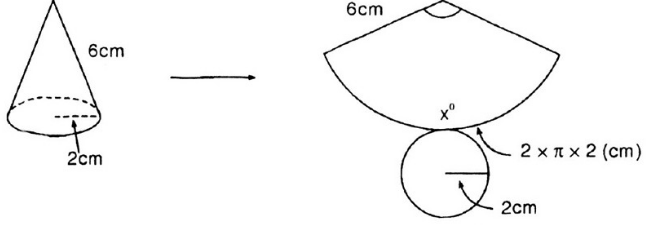
Hình 94
Lời giải
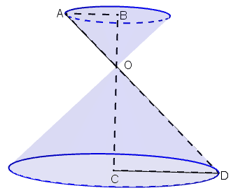
Bài 17 (trang 117 SGK Toán 9 tập 2): Khi quay tam giác vuông để tạo ra một hình nón như hình 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là 30o, độ dài đường sinh là a. Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.
Lời giải
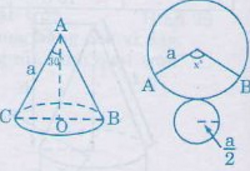
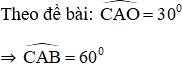
mà AB = AC
⇒ ΔABC đều
⇒ BC = AC = a
⇒ bán kính đáy hình nón: 
\(r=BO=\frac{BC}{2}=\frac{a}{2}\)
⇒ Chu vi hình tròn đáy: \(C=2\pi r=\pi a\)
Khai triển mặt xung quanh hình nón ta được hình quạt AOB có bán kính R = a.
Độ dài cung AB: 
Ta luôn có: l = C ⇒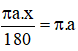 
⇒ x = 180º.
Bài 18 (trang 117 SGK Toán 9 tập 2): Hình ABCD (h.95) khi quay quanh BC thì tạo ra:
(A) Một hình trụ
(B) Một hình nón
(C) Một hình nón cụt
(D) Hai hình nón
(E) Hai hình trụ
Hãy chọn câu trả lời đúng.
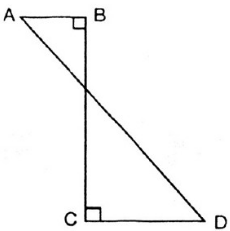
Hình 95
Lời giải
Nếu gọi O là giao điểm của BC và AD. Khi quay hình ABCD quanh BC thì có nghĩa là quay tam giác vuông OAB quanh OB và tam giác vuông OCD quanh OC. Mỗi hình quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ là hai hình nón.
Vậy chọn D.
Bài 19 (trang 118 SGK Toán 9 tập 2): Hình khai triển của mặt xung quanh của một hình nón là một hình quạt. Nếu bán kính hình quạt là 16cm, số đo cung là 120o thì độ dài đường sinh của hình nón là:
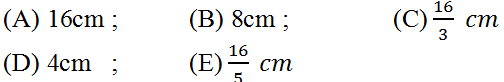
Lời giải
Khi khai triển mặt xung quanh của hình nón, ta được một hình quạt có bán kính bằng độ dài đường sinh.
Đề bài cho ta bán kính hình tròn chứa hình quạt là 16cm nên độ dài đường sinh của hình nón là 16cm.
Vậy chọn A.
Bài 20 (trang 118 SGK Toán 9 tập 2): Hãy điền đủ vào các ô trống ở bảng sau (xem hình 96):
| Bán kính đáy r(cm) | Đường kính đáy d(cm) | Chiều cao h(cm) | Độ dài đường sinh l(cm) | Thể tích V |
| 10 | 10 | |||
| 10 | 10 | |||
| 10 | 1000 | |||
| 10 | 1000 | |||
| 1000 |
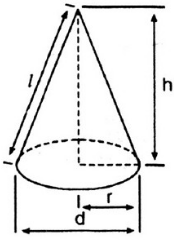
Hình 96
Lời giải
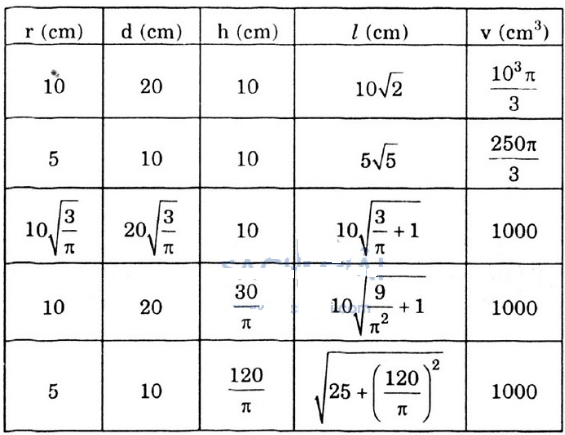
Cách tính:
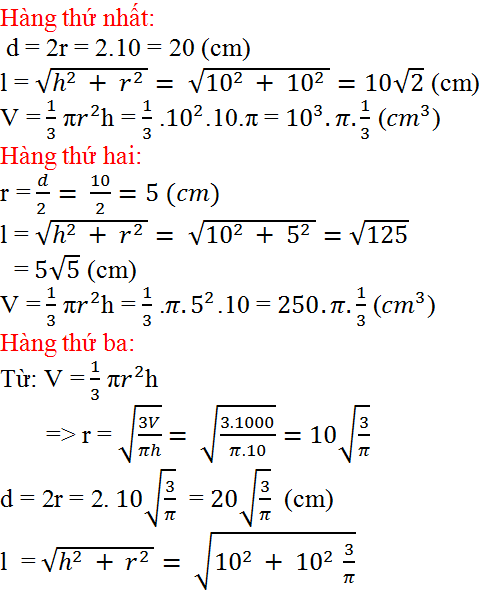
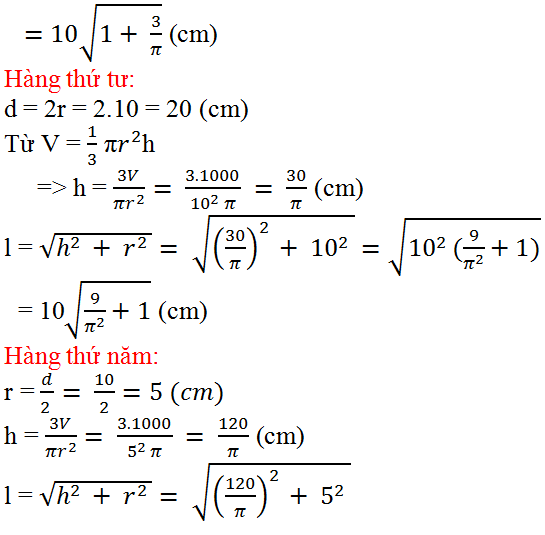
Bài 21 (trang 118 SGK Toán 9 tập 2): Cái mũ của chú hề với các kích thước cho theo hình vẽ (h.97). Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa).
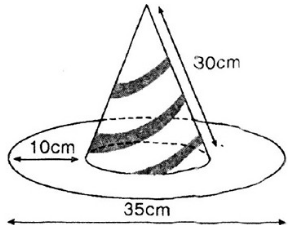
Hình 97
Lời giải
Diện tích vải cần có để làm nên cái mũ gồm diện tích xung quanh của hình nón và diện tích của vành nón.
Bán kính đường tròn đáy của hình nón: \(r=\frac{35-10-10}{2}=7,5\ \left(cm\right)\)
Diện tích xung quanh hình nón: \(S_{xq}=\pi.r.l=\pi.7,5.30=225\pi(cm^2)\)
Diện tích vành nón (hình vành khăn):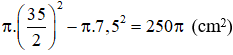 
Diện tích vải cần để may: \(225\pi+250\pi=475\pi\approx1492,3(cm^2)\)
Bài 22 (trang 118 SGK Toán 9 tập 2): Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (AO = OB).
Hãy so sánh tổng thể tích của hai hình nón và thể tích của hình trụ.
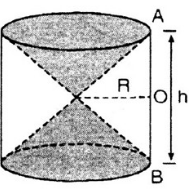
Hình 98
Lời giải
Bài 23 (trang 119 SGK Toán 9 tập 2): Viết công thức tính nửa góc ở đỉnh của một hình nón (góc α của tam giác vuông OAS – hình 99) sao cho diện tích mặt khai triển của mặt nón bằng một một phần tư diện tích của hình tròn (bán kính SA).
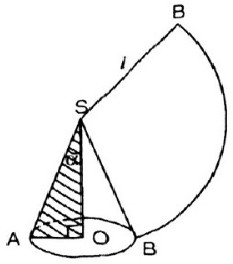
Hình 99
Lời giải
Bài 24 (trang 119 SGK Toán 9 tập 2): Hình khai triển của mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là 16cm, số đo cung là 120o. Tang của nửa góc ở đỉnh của hình nón là:
Lời giải
Bài 25 (trang 119 SGK Toán 9 tập 2): Hãy tính diện tích xung quanh của hình nón cụt biết hai ban kính đáy là a, b (a < b) và độ dài đường sinh là l (a, b, l có cùng đơn vị đo).
Lời giải
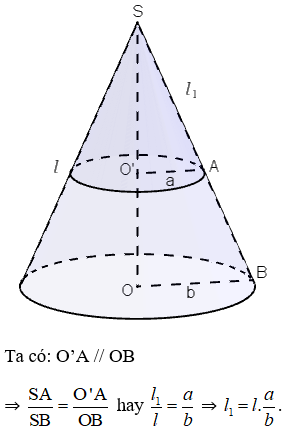
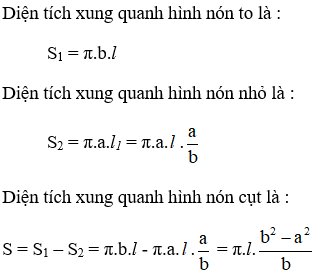
Bài 26 (trang 119 SGK Toán 9 tập 2): Hãy điền đủ vào các ô trống cho ở bảng sau (đơn vị độ dài: cm):
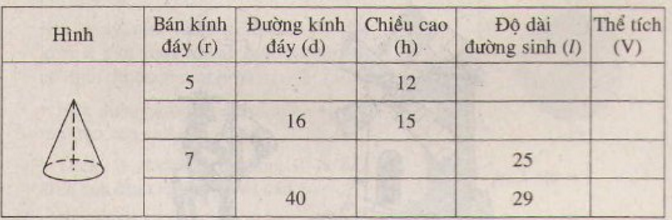
Lời giải
| Bán kính đáy r(cm) | Đường kính đáy d(cm) | Chiều cao h(cm) | Độ dài đường sinh l(cm) | Thể tích V(cm3) |
| 5 | 10 | 12 | 13 | 314 |
| 8 | 16 | 15 | 17 | 320 π |
| 7 | 14 | 24 | 25 | 392 π |
| 20 | 40 | 21 | 29 | 2800 π |
Cách tính:
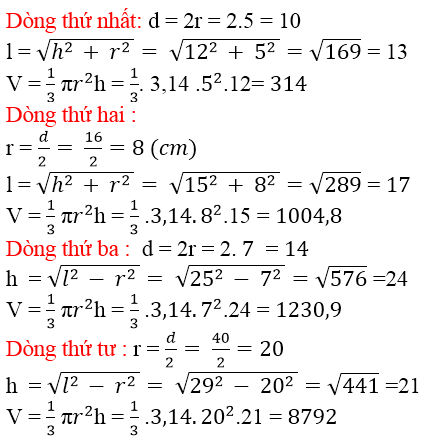
Bài 27 (trang 119 SGK Toán 9 tập 2):
a) Thể tích của dụng cụ này.
b) Diện tích mặt ngoài của dụng cụ (không tính nắp đậy).
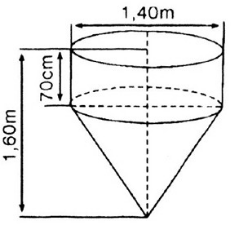
Hình 100
Lời giải
a) Thể tích hình trụ với đường kính đáy 1,4m, chiều cao 70cm = 0,7m là:
\(V=\pi r^2h=\pi.0,7^2.0,7=\frac{343}{1000}\pi\)
Thể tích hình nón, bán kính đáy bằng 0,7m, chiều cao hình nón 0,9m là:
\(V=\frac{1}{3} \pi r^2h=\frac{1}{3}\pi.0,7^2.0,9=\frac{147}{1000}\pi\)
Thể tích của dụng cụ là:
\(V=\frac{343}{1000}\pi+\frac{147}{1000}\pi=\frac{49}{100}\pi\)
b) Diện tích xung quanh hình trụ với bán kính đáy r 1,4 : 2 = 0,7m, chiều cao 70cm = 0,7m là:
\(S_{xq_{ }}=2\pi rh=2\pi\times0,7\times0,7=0,98\pi\) m2
Hình nón với bán kính đáy bằng 0,7m, chiều cao hình nón 0,9m
Đường sinh \(l=\sqrt{0,9^2+0,7^2}=\frac{\sqrt{130}}{10}\)
\(S_{xq}=\pi rl=\pi\times0,7\times\frac{\sqrt{130}}{10}\approx2,507\) m2
Diện tích mặt ngoài của dụng cụ là:
\(S=2,507\ +0,98\pi\approx5,586\ m^2\)
Bài 28 (trang 120 SGK Toán 9 tập 2): Một cái xô bằng inox có dạng hình nón cụt đựng hóa chất, có các kích thước cho ở hình 101 (đơn vị: cm).
a) Hãy tính diện tích xung quanh của xô.
b) Khi xô chứa đầu hóa chất thì dung tích của nó là bao nhiêu?
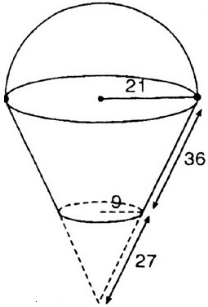
Hình 101
Lời giải
a) Diện tích cần tính gồm diện tích xung quanh của hình nón cụt và diện tích hình tròn đáy có bán kính 9cm.
Đường sinh của hình nón lớn là:
l = 36 + 27 = 63 (cm)
Diện tích xung quanh của hình nón lớn, hình nón nhỏ:
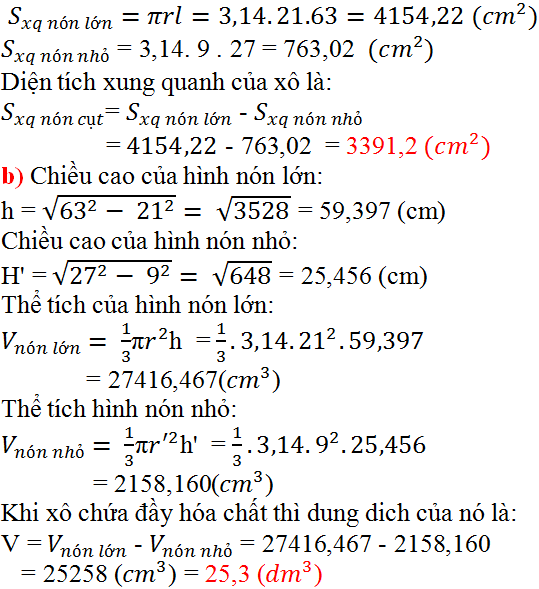
Bài 29 (trang 120 SGK Toán 9 tập 2): Cố xay gió của Đôn-ki-hô-tê (từ tác phẩm của Xéc-van-téc (Cervantès).
Phần trên của cối xay gió có dạng một hình nón (h.102). Chiều cao của hình nón là 42cm và thể tích của nó là 17 600 cm3.
Em hãy giúp chàng Đôn-ki-hô-tê tính bán kính đáy của hình nón (làm tròn kết quả đên chữ số thập phân thứ hai).
Hình 102
Lời giải
....................................
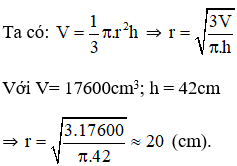
Ngoài Giải bài tập SGK Toán lớp 9 bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt
