Giải bài tập SGK Toán lớp 9 bài 3: Phương trình bậc hai một ẩn

Giải bài tập SGK Toán lớp 9 trang 40, 41 SGK

Giải bài tập Toán lớp 9 bài 3: Phương trình bậc hai một ẩn

Giải bài tập SGK Toán lớp 9 bài 3: Phương trình bậc hai một ẩn là tài liệu tham khảo hữu ích dành cho thầy cô trong quá trình giảng dạy, ôn luyện kiến thức đã học cho các bạn đồng thời cũng giúp học sinh học tốt môn Toán lớp 9. Mời các bạn tham khảo

Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 40: Trong các phương trình sau, phương trình nào là phương trình bậc hai? Chỉ rõ các hệ số a, b, c của mỗi phương trình ấy:

a) x² – 4 = 0;

b) x³ + 4x² – 2 = 0;

c) 2x² + 5x = 5;

d) 4x – 5 = 0;

e) -3x² = 0.

Lời giải

a) x² – 4 = 0: đây là phương trình bậc hai; a = 1; b = 0; c = - 4

b) x³ + 4x² – 2 = 0: đây không là phương trình bậc hai

c) 2x² + 5x = 5: đây là phương trình bậc hai; a = 2; b = 5; c = - 5

d) 4x – 5 = 0 đây không là phương trình bậc hai

e) -3x² = 0 đây là phương trình bậc hai; a = -3; b = 0; c = 0

Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 41: Giải phương trình 2x² + 5x = 0 bằng cách đặt nhân tử chung để đưa nó về phương trình tích.

Lời giải

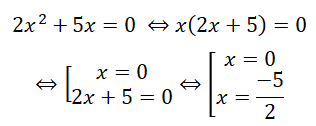
Giải bài tập SGK Toán lớp 9 bài 3: Phương trình bậc hai một ẩn

Vậy phương trình có hai nghiệm

$x_1=0$; $x_2=\frac{-5}{2}$ $x_2=\frac{-5}{2}$

Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 41: Giải phương trình: 3x² – 2 = 0.

Lời giải

$3x^2-2=0⇔3x^2=2⇔x^2=\frac{2}{3}⇔\pm x=\sqrt{\frac{2}{3}}_{ }$ $3x^2-2=0⇔3x^2=2⇔x^2=\frac{2}{3}⇔\pm x=\sqrt{\frac{2}{3}}_{ }$

Vậy phương trình có hai nghiệm

$x_1=\sqrt{\left(\frac{2}{3}\right)}$ $x_1=\sqrt{\left(\frac{2}{3}\right)}$; $x_2=-\sqrt{\left(\frac{2}{3}\right)}$ $x_2=-\sqrt{\left(\frac{2}{3}\right)}$

Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 41: Giải phương trình $(x-2)^2=\frac{7}{2}$ $(x-2)^2=\frac{7}{2}$bằng cách điền vào các chỗ trống (…) trong các đẳng thức:

$(x-2)^2=\frac{7}{2}⇔x-2=\dots⇔x=\dots$ $(x-2)^2=\frac{7}{2}⇔x-2=\dots⇔x=\dots$

Vậy phương trình có hai nghiệm là: $x_1=\dots,x_2=\dots$ $x_1=\dots,x_2=\dots$

Lời giải

$\left(x-2\right)^2=\frac{7}{2}⇔x-2\pm\sqrt{\frac{7}{2}}⇔x=2\pm\sqrt{\frac{7}{2}}$ $\left(x-2\right)^2=\frac{7}{2}⇔x-2\pm\sqrt{\frac{7}{2}}⇔x=2\pm\sqrt{\frac{7}{2}}$

Vậy phương trình có hai nghiệm

$x_1=2+\sqrt{\left(\frac{7}{2}\right)}$ $x_1=2+\sqrt{\left(\frac{7}{2}\right)}$; $x_2=2-\sqrt{\left(\frac{7}{2}\right)}$ $x_2=2-\sqrt{\left(\frac{7}{2}\right)}$

Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 41: Giải phương trình: $x^2-4x+4=\frac{7}{2}$ $x^2-4x+4=\frac{7}{2}$

Lời giải

$x^2-4x+4=\frac{7}{2}⇔\left(x-2\right)^2=\frac{7}{2}$ $x^2-4x+4=\frac{7}{2}⇔\left(x-2\right)^2=\frac{7}{2}$

$⇔x-2=\pm\sqrt{\left(\frac{7}{2}\right)}⇔x=2\pm\sqrt{\left(\frac{7}{2}\right)}$ $⇔x-2=\pm\sqrt{\left(\frac{7}{2}\right)}⇔x=2\pm\sqrt{\left(\frac{7}{2}\right)}$

Vậy phương trình có hai nghiệm

$x_1=2+\sqrt{\left(\frac{7}{2}\right)}$ $x_1=2+\sqrt{\left(\frac{7}{2}\right)}$; $x_2=2-\sqrt{\left(\frac{7}{2}\right)}$ $x_2=2-\sqrt{\left(\frac{7}{2}\right)}$

Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 41: Giải phương trình: $x^2-4x=\frac{-1}{2}$ $x^2-4x=\frac{-1}{2}$.

Lời giải

$x^2-4x=\frac{-1}{2}⇔x^2-4x+4=\frac{-1}{2}+4⇔(x-2)^2=\frac{7}{2}$ $x^2-4x=\frac{-1}{2}⇔x^2-4x+4=\frac{-1}{2}+4⇔(x-2)^2=\frac{7}{2}$

$⇔x-2=\pm\sqrt{\frac{7}{2}}⇔x=2\pm\sqrt{\frac{7}{2}}$ $⇔x-2=\pm\sqrt{\frac{7}{2}}⇔x=2\pm\sqrt{\frac{7}{2}}$

Vậy phương trình có hai nghiệm:

$x_1=2+\sqrt{\left(\frac{7}{2}\right)}$ $x_1=2+\sqrt{\left(\frac{7}{2}\right)}$; $x_2=2-\sqrt{\left(\frac{7}{2}\right)}$ $x_2=2-\sqrt{\left(\frac{7}{2}\right)}$

Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 41: Giải phương trình: $2x^2-8x=-1$

Lời giải

$2x^2-8x=-1⇔x^2-4x=\frac{-1}{2}$ $2x^2-8x=-1⇔x^2-4x=\frac{-1}{2}$

$⇔x^2-4x+4=\frac{-1}{2}+4⇔\left(x-2\right)^2=\frac{7}{2}$ $⇔x^2-4x+4=\frac{-1}{2}+4⇔\left(x-2\right)^2=\frac{7}{2}$

$⇔x-2=\pm\sqrt{\frac{7}{2}}⇔x=2\pm\sqrt{\frac{7}{2}}$ $⇔x-2=\pm\sqrt{\frac{7}{2}}⇔x=2\pm\sqrt{\frac{7}{2}}$

Vậy phương trình có hai nghiệm:

$x_1=2+\left(\sqrt{\frac{7}{2}}\right);x_2=2-\sqrt{\left(\frac{7}{2}\right)}$ $x_1=2+\left(\sqrt{\frac{7}{2}}\right);x_2=2-\sqrt{\left(\frac{7}{2}\right)}$

Bài 11 (trang 42 SGK Toán 9 tập 2): Đưa các phương trình sau về dạng ax² + bx + c = 0 và chỉ rõ các hệ số a, b, c:

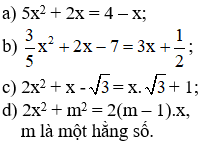
Giải bài tập SGK Toán lớp 9 bài 3: Phương trình bậc hai một ẩn

Lời giải

a) $5x^2+2x=4-x$

$⇔5x^2+2x+x-4=0$

$⇔5x^2+3x-4=0$

Phương trình bậc hai trên có a = 5; b = 3; c = -4.

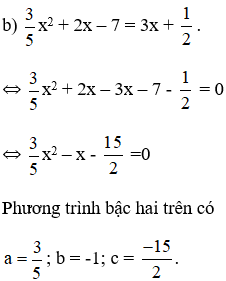
Giải bài tập SGK Toán lớp 9 bài 3: Phương trình bậc hai một ẩn

c) $2x^2+x-\sqrt{3}=x.\sqrt{3}+1$ $2x^2+x-\sqrt{3}=x.\sqrt{3}+1$

$⇔2x^2+x-x.\sqrt{3}-\sqrt{3}-1=0$ $⇔2x^2+x-x.\sqrt{3}-\sqrt{3}-1=0$

$⇔2x^2+x.\left(1-\sqrt{3}\right)-\left(\sqrt{3}+1\right)=0$ $⇔2x^2+x.\left(1-\sqrt{3}\right)-\left(\sqrt{3}+1\right)=0$

Phương trình bậc hai trên có $a=2;b=1-\sqrt{3};c=-\left(\sqrt{3}+1\right)$ $a=2;b=1-\sqrt{3};c=-\left(\sqrt{3}+1\right)$

d) $2x^2+m^2=2(m-1).x$

$⇔2x^2-2(m-1).x+m^2=0$

Phương trình bậc hai trên có a = 2; b = -2(m – 1); c = m².

Bài 12 (trang 42 SGK Toán 9 tập 2): Giải các phương trình sau:

a) $x^2-8=0$;

b) $5x^2-20=0$;

c) $0,4x^2+1=0$

d) $2x^2+\sqrt{2}x=0$ $2x^2+\sqrt{2}x=0$;

e) $-0,4x^2+1,2x=0$.

Lời giải

a) $x^2-8=0$

$⇔x^2=8$

$⇔x=2\sqrt{2}$ $⇔x=2\sqrt{2}$ hoặc $x=-2\sqrt{2}$ $x=-2\sqrt{2}$.

Vậy phương trình có hai nghiệm $x=2\sqrt{2}$ $x=2\sqrt{2}$ và $x=-2\sqrt{2}.$ $x=-2\sqrt{2}.$

b) $5x^2-20=0$

$⇔5x^2=20$

$⇔x^2=4$

$⇔x=2$ hoặc $x=-2$.

Vậy phương trình có hai nghiệm $x=2$ và $x=-2$.

c) $0,4x^2+1=0$

$⇔0,4x^2=-1$

$⇔x^2=\frac{-10}{4}$ $⇔x^2=\frac{-10}{4}$

Phương trình vô nghiệm vì $x^2\ge0$ $x^2\ge0$ với mọi x.

d) $2x^2+x\sqrt{2}=0$ $2x^2+x\sqrt{2}=0$

$⇔x.\sqrt{2}.(x\sqrt{2}+1)=0$ $⇔x.\sqrt{2}.(x\sqrt{2}+1)=0$

$⇔x=0$ hoặc $x\sqrt{2}+1=0$ $x\sqrt{2}+1=0$

$+x\sqrt{2}+1=0⇔$ $+x\sqrt{2}+1=0⇔$ $x=\frac{-1}{\sqrt{2}}$ $x=\frac{-1}{\sqrt{2}}$

Vậy phương trình có hai nghiệm x = 0 và $x=\frac{-1}{\sqrt{2}}$ $x=\frac{-1}{\sqrt{2}}$

e) $-0,4x^2+1,2x=0$

$⇔-0,4x.(x-3)=0$

$⇔x=3$ hoặc $x-3=0$

$+x-3=0⇔x=3$.

Vậy phương trình có hai nghiệm $x=0$ và $x=3$.

Bài 13 (trang 43 SGK Toán 9 tập 2): Cho các phương trình:

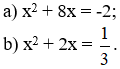
Giải bài tập SGK Toán lớp 9 bài 3: Phương trình bậc hai một ẩn

Hãy cộng vào hai vế của mỗi phương trình cùng một số thích hợp để được một phương trình mà vế trái thành một bình phương.

Lời giải

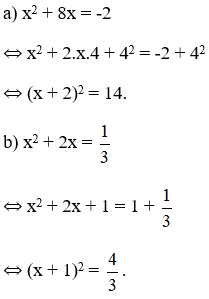
Giải bài tập SGK Toán lớp 9 bài 3: Phương trình bậc hai một ẩn

Bài 14 (trang 43 SGK Toán 9 tập 2): Hãy giải phương trình: $2x^2+5x+2=0$ theo các bước như ví dụ 3 trong bài học.

Lời giải

(Lưu ý: Các phần giải thích các bạn có thể không trình bày vào bài làm)

$2x^2+5x+2=0$

$⇔2x^2+5x=-2$ (Chuyển 2 sang vế phải)

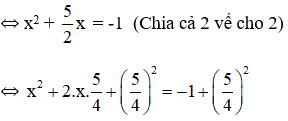
(Tách $\frac{5}{2}x$ $\frac{5}{2}x$ thành $2.x.\frac{5}{4}$ $2.x.\frac{5}{4}$ và thêm bớt $\left(\frac{5}{4}\right)^2$ $\left(\frac{5}{4}\right)^2$ để vế trái thành bình phương).

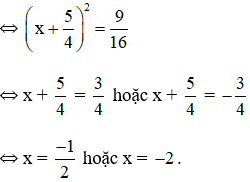
Vậy phương trình có hai nghiệm

....................................

Ngoài Giải bài tập SGK Toán lớp 9 bài 3: Phương trình bậc hai một ẩn. Mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Chia sẻ, đánh giá bài viết

5

2.794

Bài trước

Bài sau