VnDoc.com

Giải Toán 9 bài 5: Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

Giải SGK Toán 9 trang 58, 59 tập 1

Bài trước

Bài sau

Giải SGK Toán 9 bài 5: Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

Lý thuyết hệ số góc của đường thẳng y = ax + b (a ≠ 0)
Câu hỏi trang 56 SGK Toán 9 tập 1
Giải bài tập trang 58, 59 SGK Toán lớp 9 tập 1
Bài 28 trang 58 sgk toán 9 tập 1
Bài 29 trang 59 sgk toán 9 tập 1
Bài 30 (trang 59 SGK Toán 9 tập 1)

Giải SGK Toán 9 bài 5: Hệ số góc của đường thẳng y = ax + b (a ≠ 0) hướng dẫn giải chi tiết cho các câu hỏi trong SGK Toán 9 giúp các em nắm vững kiến thức trong bài, từ đó luyện giải Toán 9 hiệu quả.

Lý thuyết hệ số góc của đường thẳng y = ax + b (a ≠ 0)

1. Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục O.

Gọi A là giao điểm của đường thẳng y = ax + b với Ox và T là một điểm thuộc đường thẳng, nằm phía trên trục Ox. Khi đó góc TAx được gọi là góc tạo bởi đường thẳng y = ax + b và trục Ox.

2. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

Khi a > 0, góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn và nếu a càng lớn thì góc đó càng lớn.

Khi a < 0, góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù và nếu a càng bé thì góc đó càng lớn.

Như vậy, góc tạo bởi đường thẳng y = ax + b và trục Ox phụ thuộc vào a.

Người ta gọi a là hệ số góc của đường thẳng y = ax + b.

Câu hỏi trang 56 SGK Toán 9 tập 1

Hình 11a) biểu diễn đồ thị của các hàm số (với hệ số a > 0)

y = 0,5x + 2;

y = x + 2;

y = 2x + 2.

Hình 11b) biểu diễn đồ thị của các hàm số (với hệ số a < 0):

y = -2x + 2;

y = -x + 2;

y = -0,5x + 2.

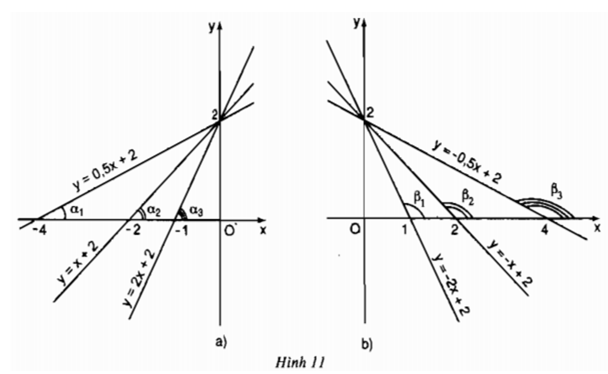
Câu hỏi trang 56 SGK Toán 9 tập 1

a) Hãy so sánh các góc α₁, α₂, α₃và so sánh các giá trị tương ứng của hệ số a trong các hàm số (trường hợp a > 0) rồi rút ra nhận xét.

b) Cũng làm tương tự như câu a) với trường hợp a > 0.

Hướng dẫn giải

a) Ta có: α₁< α₂< α₃ và các giá trị tương ứng của hệ số a trong các hàm số :

0,5 < 1 < 2

Nhận xét: Khi hệ số a dương (a > 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 90^o

b) Ta có: β₁< β₂< β₃ và các giá trị tương ứng của hệ số a trong các hàm số

-2 < -1 < -0,5

Nhận xét: Khi hệ số a âm (a < 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 180^o

Giải bài tập trang 58, 59 SGK Toán lớp 9 tập 1

Bài 27 trang 58 sgk toán 9 tập 1

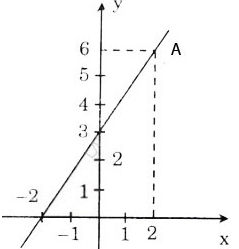
Cho hàm số bậc nhất y = ax + 3.

a) Xác định hệ số góc a, biết rằng đồ thị của hàm số đi qua điểm A(2; 6).

b) Vẽ đồ thị của hàm số.

Hướng dẫn giải:

a) Vì đồ thi của hàm số đi qua điểm A(2; 6) nên ta có 6 = a . 2 + 3.

Suy ra hệ số góc a = 1,5.

b) Hàm số đã cho là y = 1,5x + 3. Đồ thị được vẽ như hình bên.

Giải bài tập trang 58, 59 SGK Toán lớp 9 tập 1

Bài 28 trang 58 sgk toán 9 tập 1

Cho hàm số y = -2x + 3.

a) Vẽ đồ thị của hàm số.

b) Tính góc tạo bởi đường thẳng y = -2x + 3 và trục Ox (làm tròn đến phút).

Hướng dẫn giải:

a) Vẽ đồ thị hàm số:

- Cho x = 0 thì y = 3 ta được A(0; 3)

Cho y = 0 thì x = 3/2 ta được B(3/2; 0)

b) Gọi góc hợp bởi đường thẳng y = -2x + 3 và trục Ox là α.

Ta có: $\alpha = \widehat {ABx}$ $\alpha = \widehat {ABx}$. Xét tam giác vuông OAB ta có:

$\tan \widehat {OBA} = \frac{{OA}}{{OB}} = \dfrac{3}{{\dfrac{3}{2}}} = 2 \Rightarrow \widehat {OBA} \approx {63^0}26$ $\tan \widehat {OBA} = \frac{{OA}}{{OB}} = \dfrac{3}{{\dfrac{3}{2}}} = 2 \Rightarrow \widehat {OBA} \approx {63^0}26'$

Vậy $\alpha = {180^0} - \widehat {OBA} \approx {116^0}34$ $\alpha = {180^0} - \widehat {OBA} \approx {116^0}34'$

Bài 29 trang 59 sgk toán 9 tập 1

Xác định hàm số bậc nhất y = ax + b trong mỗi trường hợp sau:

a) a = 2 và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5.

b) a = 3 và đồ thị của hàm số đi qua điểm A(2; 2).

c) Đồ thị của hàm số song song với đường thẳng y = √3x và đi qua điểm B(1; √3 + 5).

Hướng dẫn giải:

a. Với _{$a=2\Rightarrow y=2x+b$} (1)

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1,5

_{$\Rightarrow y=0,x=1,5$} (2)

Từ (1) và (2) ta có:

$0=2.1,5+b\Rightarrow b=-3$ $0=2.1,5+b\Rightarrow b=-3$

Vậy hàm số đã cho là y = 2x – 3

b. Với _{$a=3\Rightarrow y=3x+b$} (3)

Đồ thị hàm số đi qua điểm A(2, 2)

_{$\Rightarrow y=2,x=2$} (4)

Từ (3) và (4) ta có:

$2=3.2+b\Rightarrow b=2-3.2=-4$ $2=3.2+b\Rightarrow b=2-3.2=-4$

Vậy hàm số đã cho là y = 3x – 4

c. Đồ thị hàm số song song với đường thẳng _{$y=\sqrt{3}x$}

_{$\Rightarrow a=\sqrt{3}\Rightarrow y=\sqrt{3}x+b$} (5)

Đồ thị đi qua điểm _{$B\left( 1;\sqrt{3}+5 \right)$}

_{$\Rightarrow x=1,y=\sqrt{3}+5$} (6)

Từ (5) và (6) ta có:

$\Rightarrow \sqrt{3}+5=\sqrt{3}.1+b\Rightarrow b=5$ $\Rightarrow \sqrt{3}+5=\sqrt{3}.1+b\Rightarrow b=5$

Vậy hàm số đã cho là: _{$y=\sqrt{3}x+5$}

Bài 30 (trang 59 SGK Toán 9 tập 1)

a. Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:

$y=\frac{1}{2}x+2$ $y=\frac{1}{2}x+2$

$y=-x+2$

b. Gọi giao điểm của hai đường thẳng _{$y=\frac{1}{2}x+2$} và _$y=-x+2$ với trục hoành theo thứ tự A, B và gọi giao điểm của hai đường thẳng đó là C. Tính các góc của tam giác ABC (làm tròn đến độ)

c. Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet).

Hướng dẫn giải:

a. Đồ thị hàm số: _{$y=\frac{1}{2}x+2$}

Chọn $\left\{ \begin{matrix} x=0\Rightarrow y=2\text{ } \\ x=-4\text{ }\Rightarrow \text{ }y\text{ }=\text{ }0 \\ \end{matrix} \right.$ $\left\{ \begin{matrix} x=0\Rightarrow y=2\text{ } \\ x=-4\text{ }\Rightarrow \text{ }y\text{ }=\text{ }0 \\ \end{matrix} \right.$

Đồ thị hàm số _$y=-x+2$

Chọn _{$\left\{ \begin{matrix}

x=0\Rightarrow y=2 \\

x=2\Rightarrow y=0 \\

\end{matrix} \right.$}

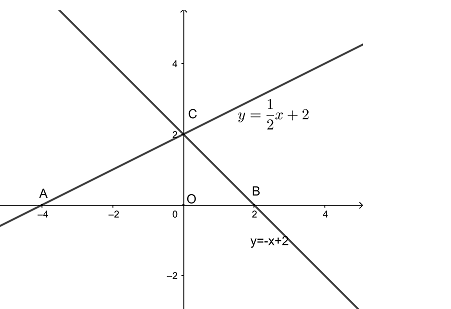
Bài 30 trang 59 SGK Toán 9 tập 1

b. Phương trình hoành độ giao điểm là nghiệm của phương trình:

$\frac{1}{2}x+2=-x+2\Rightarrow x=0$ $\frac{1}{2}x+2=-x+2\Rightarrow x=0$

Thay _$x=0$ vào _{$y=\frac{1}{2}x+2$} ta được _$y=2$

$\Rightarrow C\left( 0,2 \right)$ $\Rightarrow C\left( 0,2 \right)$

Xét tam giác vuông OAC vuông tại O ta có:

$\tan \widehat{CAO}=\frac{\left| OC \right|}{\left| OA \right|}=\frac{2}{4}=\frac{1}{2}\Rightarrow \widehat{CAO}={{26}^{0}}33$ $\tan \widehat{CAO}=\frac{\left| OC \right|}{\left| OA \right|}=\frac{2}{4}=\frac{1}{2}\Rightarrow \widehat{CAO}={{26}^{0}}33'$

Áp dụng định lý Py – ta – go

$\begin{align} & O{{A}^{2}}+O{{C}^{2}}=A{{C}^{2}} \\ & \Rightarrow AC=\sqrt{O{{A}^{2}}+O{{C}^{2}}}=\sqrt{{{4}^{2}}+{{2}^{2}}}=2\sqrt{5} \\ \end{align}$ $\begin{align} & O{{A}^{2}}+O{{C}^{2}}=A{{C}^{2}} \\ & \Rightarrow AC=\sqrt{O{{A}^{2}}+O{{C}^{2}}}=\sqrt{{{4}^{2}}+{{2}^{2}}}=2\sqrt{5} \\ \end{align}$

Xét tam giác vuông OBC vuông tại O ta có:

$\tan \widehat{CBO}=\frac{\left| OC \right|}{\left| OB \right|}=\frac{2}{2}=1\Rightarrow \widehat{CBO}={{45}^{0}}$ $\tan \widehat{CBO}=\frac{\left| OC \right|}{\left| OB \right|}=\frac{2}{2}=1\Rightarrow \widehat{CBO}={{45}^{0}}$

Áp dụng định lý Py – ta – go

$\begin{align} & O{{B}^{2}}+O{{C}^{2}}=C{{B}^{2}} \\ & \Rightarrow BC=\sqrt{O{{B}^{2}}+O{{C}^{2}}}=\sqrt{{{2}^{2}}+{{2}^{2}}}=2\sqrt{2} \\ \end{align}$ $\begin{align} & O{{B}^{2}}+O{{C}^{2}}=C{{B}^{2}} \\ & \Rightarrow BC=\sqrt{O{{B}^{2}}+O{{C}^{2}}}=\sqrt{{{2}^{2}}+{{2}^{2}}}=2\sqrt{2} \\ \end{align}$

Xét tam giác ABC có

AB = OA + OB = 4 + 2 = 6

$\begin{align} & \widehat{CAO}+\widehat{CBO}+\widehat{ACB}={{180}^{0}} \\ & \Leftrightarrow \widehat{ACB}={{180}^{0}}-\widehat{CAO}-\widehat{CBO} \\ & \Leftrightarrow \widehat{ACB}={{180}^{0}}-{{26}^{0}}33$ $\begin{align} & \widehat{CAO}+\widehat{CBO}+\widehat{ACB}={{180}^{0}} \\ & \Leftrightarrow \widehat{ACB}={{180}^{0}}-\widehat{CAO}-\widehat{CBO} \\ & \Leftrightarrow \widehat{ACB}={{180}^{0}}-{{26}^{0}}33'-{{45}^{0}}={{108}^{0}}27' \\ \end{align}$

c. Diện tích tam giác ABC: _{$S=\frac{1}{2}.OC.AB=\frac{1}{2}.2.6=6$}

Chu vi tam giác ABC: _{$CV=AB+AC+CB=6+2\sqrt{5}+2\sqrt{2}$}

....................................

Ngoài tài liệu trên, mời các bạn tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi học kì 2 lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt.

Bài tiếp theo